KNN算法
文章目录
- 一、 问题举例
- 二、算法描述
- 1、最近邻法
- 2、K-近邻法
- 3、解决思路
- 三、结果
- 1、Iris 数据集
- 2、Sonar 数据集
- 3、USPS手写体数据集
- 4、对比算法:Fisher+k近邻
- 四、总结
- 五、代码
一、 问题举例
用KNN对数据集进行分类
1)USPS 手写体
2)UCI 数据库中 sonar 数据源
3)UCI 数据库中 Iris 数据
验证算法:不进行降维
- K 近邻方法分类
- 最近邻方法分类
- 对比算法:Fisher + K 近邻(最近邻)
二、算法描述
1、最近邻法
对于一个新样本,把它逐一与已知样本比较,找出距离新样本最近的已知 样本,以该样本的类别作为新样本的类别。
这种做法可以表述为:已知样本集 SN = {( x 1, θ 1)},( x 2, θ 2)}, ( x 3, θ 3)…, ( x N, θ N)},其中 xi 是样本 i 的特征向量, θ i 是它对应的类别,设有 C 个类,即θ i∈{1,2,3,…,C}。定义两个样本间的距离度量 δ(xi,xj),比 如可以采用欧式距离 δ(xi,xj) = ||xi - xj||。对未知的样本 x,求 SN 中与之 距离最近的样本,设为 x’(对应的类别为 θ ’ ),即
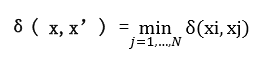 则将 x 决策为θ ’ 类。
则将 x 决策为θ ’ 类。
这种决策方法称作最近邻决策。 如果写成判别函数的形式, ω i 类的判别函数可写作
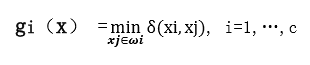 决策规则为各类判别函数比较大小,即
决策规则为各类判别函数比较大小,即
![]()
2、K-近邻法
在很多情况下,把决策建立在最近的一个样本上有一定的风险,当数据分布 复杂或数据中噪声严重时尤其如此。
一种很自然的改进就是引入投票机制,选择前若干个离新样本最近的已知样 本,用它们的类别投票来决定新样本的类别,这种方法称为 k-近邻法,因为人们 习惯上把参加投票的近邻样本的个数记作 k。显然,最近邻法可以看作是 k-近邻 法的特例,因此也有人把它称作 1-近邻法(k=1).
K-近邻法可以表示为:设有 N 个已知样本分属于 c 个类 ω i,i=1,…,c,考 查新样本 x 在这些样本中的前 k 个近邻,设其中有 ki 个属于 ω i 类,则 ω i 类的 判别函数就是
![]()
决策规则是
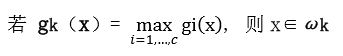
3、解决思路
以 sonar 数据集为例,一共有 2 类,第一类有 97 个样本,第二类有 111 个 样本,算法步骤如下:
1)取数据集的第 i 个样本作为测试(i 的初始值为 1),剩下的所有 207 个 样本将作为训练集。
2)将测试样本和训练集的每一个样本求欧式距离,和该训练样本的类别标 签存在一个数组中。
3)将数组按照欧式距离进行排序,取前 k 个最小的训练样本。
4)统计筛选出来的训练样本的类别标签,得到出现次数最多的标签,作为 测试集的预测值。
5)将预测值与测试样本的真实标签比较,若一致,则预测成功。
6)i=i+1,重复步骤 1),直到 i=208,得到 k 近邻算法分类的准确率。
三、结果
1、Iris 数据集
将 k 分别取 1 至 50,得到 k 在不同的取值下的近邻法准确率,绘出 k 和准确率的关系图像
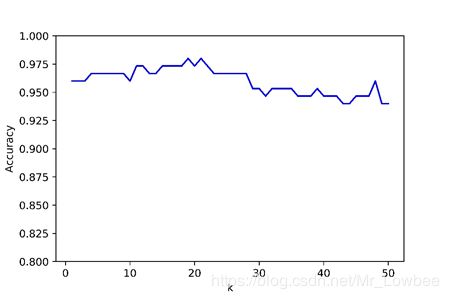
可以看到,当 k 取 20 的时候,准确率最高,但总体来看准确率还是能达到 95%以上,分类效果较好。
将 k 取 1,k 近邻就变为 1-近邻,即得到最近邻的分类准确率约为 0.96 ,代码部分放在最后。
2、Sonar 数据集
将 k 分别取 1 至 100,得到 k 在不同的取值下的近邻法准确率,绘出 k 和 准确率的图像

从图中可以看到,当 k 取 0 到 10 时,近邻法识别的准确率最高,能够达到 80%以上,随着 k 的增大,准确率稳定在 70%左右
将 k 取 1,得到最近邻的识别准确率约为 0.83 ,代码部分放在最后。
3、USPS手写体数据集
USPS手写体数据集有0到9一共十类,在进行数据处理时,已经将原来图片的16*16像素转化为256个灰度值,即USPS中的每个样本一共有256维特征,数据集分为训练样本7291个和测试样本2007个,训练标签和测试标签。
将k分别取1至20,得到k在不同的取值下的近邻法准确率,绘出k和准确率的图
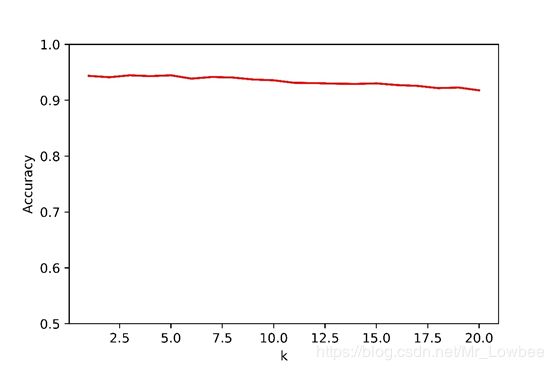
可以看到,在 k 取 0 到 20 时,k 近邻法分类的准确率基本维持在 93%左右
将 k 取 1,得到最近邻的识别准确率约为 94%
4、对比算法:Fisher+k近邻
取Sonar数据集的Fisher和k近邻分类算法准确率进行对比
在上一篇博客中,我们分别取了sonar数据集的1到60维的特征进行线性判别,在得出最优投影方向W*(d维列向量)之后利用分类阈值W0和决策规则g(x)可以得到分类准确率。
Fisher判别的准确率如下:
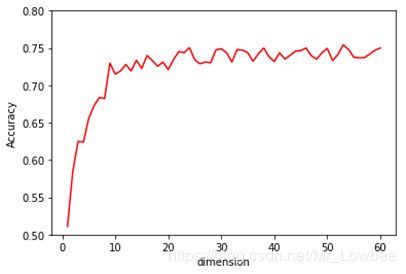
从图中可以看出,当选取的特征维数较少的时候,Fisher线性判别准确率只有50%至60%,但在选取的特征维数较多时,分类准确率可以达到70%至75%
k-近邻的准确率如下:
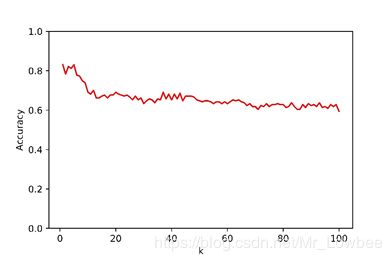
从k-近邻的图像中可以看到,准确率呈现出和Fisher相反的趋势,在k取较小的时候得到的准确率可达80%以上,甚至最近邻方法的分类准确率可以达到83%。但当k取较大值之后,准确率反而下降了,维持在70%左右.
四、总结
1、使用最近邻方法能够得到最高的准确率,其效果要比Fisher线性判别的结果好。当将k增大的时候,k-近邻的方法反而不如Fisher判别方法准确率高了。总体来说,k-近邻的判别方法要稳定一些。
2、k-近邻方法思路简单,算法过程清晰,但是计算过程十分繁琐。因为对于每一个测试样本,都要对其与每一个训练样本求欧式距离,之后再进行排序,而排序的算法需要耗费大量时间,再取前k小个欧式距离的类别标签,得出预测标签。这样,对于USPS手写体这样维数高、样本个数多的数据集,k-近邻方法显然不是一种节约时间的方法。
3、Fisher线性判别虽然算法过程略微复杂一些,而且涉及到矩阵求逆,矩阵求积等时间和空间复杂度都非常高的计算。但是只要训练过程一旦完成,我们能够得到一个最佳投影方向W*,对于所有的测试样本,不用再一一进行计算了,直接利用决策函数进行判别就可以。也就是说,k-近邻的方法根本不存在训练过程,每一次的判别都要重复进行计算,而Fisher线性判别只需要进行一次训练过程,大大省去了测试过程的计算时间。所以,针对训练集数据样本非常多的情况,Fisher线性判别是一种更加优越的方法。
4、对于多分类的情况,k-近邻完全可以不管数据集的类别个数,因为k-近邻是用所有样本与测试集的欧式距离来判断测试类别,无论数据类别有多少,k-nn只取前k个最近欧式距离投票的结果,而且结果只会有一个标签,也就是说,k-近邻方法根本不需要降维。而对于Fisher线性判别,课本中只提到了二分类的情况,对于多分类的问题,Fisher线性判别需要将多维特征降维到能够进行线性判别的维度,决策规则也需要重新定义,大大增加了计算复杂度。所以对于数据集类别较多的情况,k-近邻判别方法具有明显的优势。
五、代码
实验环境Python3.6
GitHub地址如下
Pattern recognition / KNN
https://github.com/Fangzhenxuan/AI_Projects.git