利用Python语言实现多幅图像拼接创建全景图

一、明确图像拼接整体流程

1. 提供一组图像集，实现特征匹配(相邻图像之间要有重复区域)
2. 通过匹配特征计算图像之间的变换结构
3. 利用图像变换结构，实现图像映射
   扩展:
4. 针对叠加后的图像，采用APAP之类的算法，对齐特征点
5. 通过图割方法，自动选取拼接缝

1.1实现图像集之间的特征匹配

关于使用SIFT特征实现图像之间的特征匹配原理及例子请阅读这篇博文(https://mp.csdn.net/mdeditor/88585677#)，这里便不再详细解释了。
在本实验中，如下代码能够实现特征匹配

import sift
featname = ['D:输入图片/Univ'+str(i+1)+'.sift' for i in range(5)] 
imname = ['D:输入图片/Univ'+str(i+1)+'.jpg' for i in range(5)]
l = {}
d = {}
for i in range(5): 
    sift.process_image(imname[i],featname[i])
    l[i],d[i] = sift.read_features_from_file(featname[i])
    
matches = {}
for i in range(4):
    matches[i] = sift.match(d[i+1],d[i])

实现结果如下所示:

1.2使用RANSAC求解单应性矩阵

RANSAC(Random Sample Consensus)即随机采样一致性，对SIFT算法产生的128维特征描述符进行剔除错误匹配点。
它的基本思想是:数据中包含正确的点和噪声点，给定一个合理的模型，这个模型应该能够在描述正确数据点的同时摒弃噪声点。
在本实验中，在上一步特征匹配获得的匹配点对中抽取几对匹配点，计算变换矩阵，并将这几对点记录为”inliers”。继续寻找配准点对中的"outliers"，若这些配准点对符合矩阵，则将其添加到"inliers"。当"inliers"中的点对数大于设定阈值时，则判定此矩阵为精确的变换矩阵。依照以上方法，随机采样 N 次，选取"inliers"数最大集合，剔除"outliers"等误配点对。
实现此功能的代码如下:

class RansacModel(object):
   
   def __init__(self,debug=False):
        self.debug = debug
   def fit(self, data):
   #计算选取的4个对应点对，拟合一个单应性矩阵。
   
        #将这些矩阵转置，来调用H_from_points()计算单应性矩阵
        data = data.T

        #映射的起始点
        fp = data[:3,:4]

        #映射的目标点
        tp = data[3:,:4]

        #计算单应性矩阵，然后返回
        return H_from_points(fp,tp)
        
   def get_error( self, data, H):
   #对所有的对应点计算单应性矩阵，然后对每个变换后的点，返回相应的误差
   
        data = data.T

        #映射的起始点
        fp = data[:3]

        #映射的目标点
        tp = data[3:]

        #变换fp
        fp_transformed = dot(H,fp)

        #归一化齐次坐标
        fp_transformed = normalize(fp_transformed)

        #返回每个点的误差
        return sqrt( sum((tp-fp_transformed)**2,axis=0) )

fit()方法对选择的4个点对拟合一个单应性矩阵。get_error()方法对每个对应点对使用该单应性矩阵，然后返回相应的平方距离之和，所以RANSAC算法能够判断哪些点对是正确的，哪些是错误的。

之前也说过，还需要设置一个阈值，来决定哪些单应性矩阵是合理的。
代码如下:

def H_from_ransac(fp,tp,model,maxiter=1000,match_theshold=10):

    from PCV.tools import ransac

    data = vstack((fp,tp))

    H,ransac_data = ransac.ransac(data.T,model,4,maxiter,match_theshold,10,return_all=True)
    
    return H,ransac_data['inliers']

该函数最重要的参数是最大的迭代次数，程序退出去太早可能得到一个坏解，迭代次数太多会占用太多时间。 最后结果是返回单应性矩阵和对应该单应性矩阵的正确点对。

1.3拼接图像

经过之前的步骤，已经估计出图像间的单应性矩阵，现在要将所有的图像扭曲到一个公共平面上。通常，这里的公共平面为中心图像平面(否则，需要进行大量变形)。一种方法是创建一个很大的图像，比如图像中全部填充0，使其和中心图像平行，然后将所有的图像扭曲到上面。本实验使用的是较为简单的步骤:将中心图像左边或者右边的区域填充0，以便为扭曲的图像腾出空间。
代码如下:

def panorama(H,fromim,toim,padding=2400,delta=2400):
#使用单应性矩阵H，协调两幅图片，创建水平全景图像，结果为一幅和toim具有相同高度的图像。padding指定填充像素的数目，delta指定额外的平移量。

      #检查图像是灰度图像还是彩色图像
      is_color = len(fromim.shape) == 3

     def transf(p):
        p2 = dot(H,[p[0],p[1],1])
        return (p2[0]/p2[2],p2[1]/p2[2])
    
     if H[1,2]<0: #fromin在右边
        print ('warp - right')       
        if is_color:#如果是彩色图像
          #在目标图像的右边填充0
           toim_t = hstack((toim,zeros((toim.shape[0],padding,3))))
           fromim_t = zeros((toim.shape[0],toim.shape[1]+padding,toim.shape[2]))
           for col in range(3):
                fromim_t[:,:,col] = ndimage.geometric_transform(fromim[:,:,col],
                                        transf,(toim.shape[0],toim.shape[1]+padding))
    
        else：#如果是灰度图像
            #在目标图像的右边填充0
            toim_t = hstack((toim,zeros((toim.shape[0],padding))))
            fromim_t = ndimage.geometric_transform(fromim,transf,
                                    (toim.shape[0],toim.shape[1]+padding)) 

     else:#fromin在左边
        print ('warp - left') 

       #为了填充补偿效果，在左边加入平移量   
        H_delta = array([[1,0,0],[0,1,-delta],[0,0,1]])
        H = dot(H,H_delta)
        在目标图像左边填充0的代码与上述类似，便不再列出。

transf()函数通过将像素和单应性矩阵H相乘，然后对齐次坐标进行归一化来实现像素间的映射。注意：当填充区域在目标图像的左边时，这时，目标图像的坐标也随之右移，所以在这种情况下，需要在单应性矩阵中加入平移。

最后操作：将fromin放置在toim上，代码如下：

if is_color:
   alpha = ((fromim_t[:,:,0] * fromim_t[:,:,1] * fromim_t[:,:,2] ) > 0)
        for col in range(3):
            toim_t[:,:,col] = fromim_t[:,:,col]*alpha + toim_t[:,:,col]*(1-alpha)
else:
        alpha = (fromim_t > 0)
        toim_t = fromim_t*alpha + toim_t*(1-alpha)
        
 return toim_t

这里再次使用了alpha通道方法，原理再回顾一下:
alpha通道方法是设置toim的目标区域部分值为1，其他区域值为0，(0是背景为黑色，1是前景为白色)，先映射出一张和toim一样的图像a(相当于先建立一个蒙板)，然后在蒙板里把不需要的地方填充成黑色，需要的地方即目标区域留成白色，这个时候实际上是做了一次乘法。用黑色所代表的数值0去乘以toim ，那么这个地方就变透明了，用白色所代表的数值乘以目标区域，再将两者相加，这样fromin就能贴在toim的目标区域上。

最后实现的全景拼接图如下:

1.4根据上述方法实现的例子

1.4.1一组室内图像

最后拼接的全景图：

在运行程序时出现了错误:did not meet fit acceptance criteria,原因为最初我在拍摄一组图像时，并不是从同一视角出发拍摄所有图像，也就是说你需要站在同一个地点从左往右拍摄图像，而不能在拍摄的同时随着拍摄景物的移动身体也跟着移动。
记住拍摄完图像之后，要将图像从右往左排序，因为匹配是从最右边的图像开始计算出来的。
这组图像拼接效果不好，整体往左边扭曲了。

1.4.2一组室外景深落差较大的图像

最后拼接的全景图：

这组输入的图像较为清晰，相邻两张图像重复区域适中，并且没有过于相似的建筑物，所以在特征匹配的时候错误匹配较少，拼接的全景图也较为令人满意。当然不足的地方还是有的，比如拼接缝过于明显且不同区域曝光度不同，这些都是需要后期再进行处理的。

1.4.3一组室外景深落差较小的图像

最后拼接的全景图：

如结果所示这只是完成了拼接，清晰度等其他细节处处理的并不好，与上一组图像相比较可以得知，进行图像拼接的原素材图像也是非常重要的。但是，这最后两组图像并未像第一组图像那样在拼接后形成了一张扭曲的全景图。

1.5扩展:如何消除图像拼接中的"鬼影"现象

可以使用APAP(As-Projective-As-Possible)算法，此算法是将图像切割成无数多个小方块，对每个小方块的单应性矩阵逐一估计。指路这条博文(https://blog.csdn.net/xuanwu_yan/article/details/9400321)里面较为详细地介绍了APAP算法的原理。

1.6扩展:如何选取最佳拼接缝

寻找最佳拼接缝算法中，Graph Cut很经典。它将计算机视觉问题和网络流联系在一起。寻找最佳拼接缝等价于求网络流的最小割。 在网络流问题中，最小割和最大流相等。
1.首先介绍最小割问题
一个有向图，并有一个源顶点（source vertex）和目标顶点（target vertex）.边的权值为正,又称之为容量（capacity）.如下图

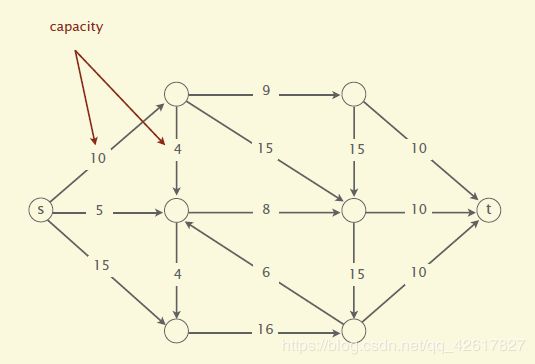
一个st-cut(简称割cut)会把有向图的顶点分成两个不相交的集合，其中s在一个集合中，t在另外一个集合中。
这个割的容量（capacity of the cut）就是A到B所有边的容量和。注意这里不包含B到A的。参见下面几幅图。最小割问题就是要找到割容量最小的情况。

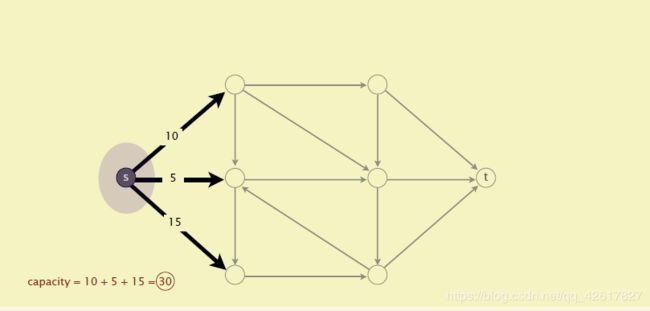
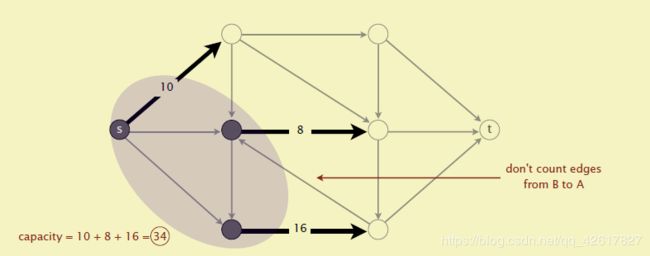
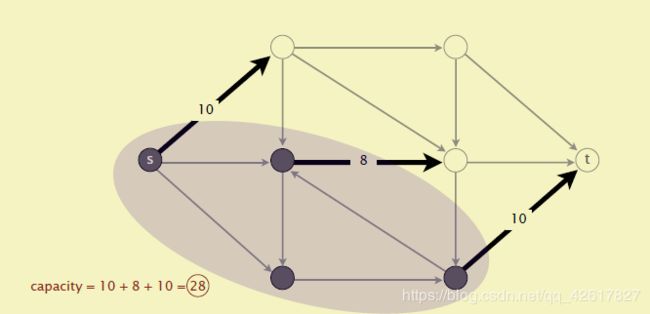
2.介绍最大流问题
跟mincut问题类似，maxflow要处理的情况也是一个有向图，并有一个原顶点（source vertex）和目标（target vertex）.边的权值为正,又称之为容量（capacity）.如下图

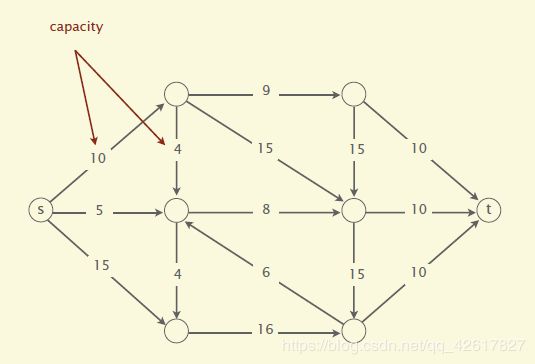
一个st-flow(简称flow)是为每条边附一个值，这个值需要满足两个条件1 0<=边的flow <<边的capacity2 除了s和t外，每个顶点的inflow要等于outflow

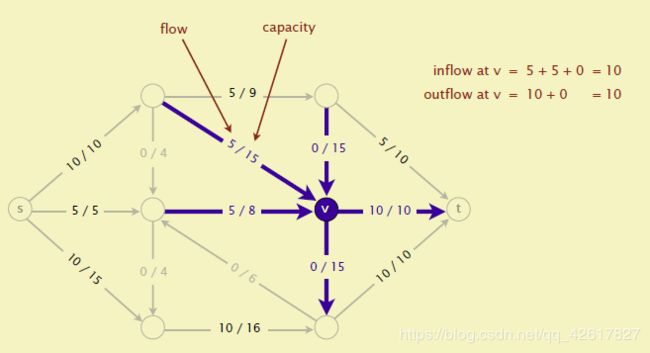
一个flow的值（value of the flow）就是t的inflow.Maxflow就是找到这个最大值。


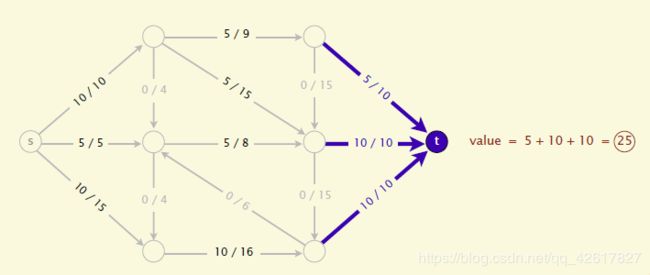
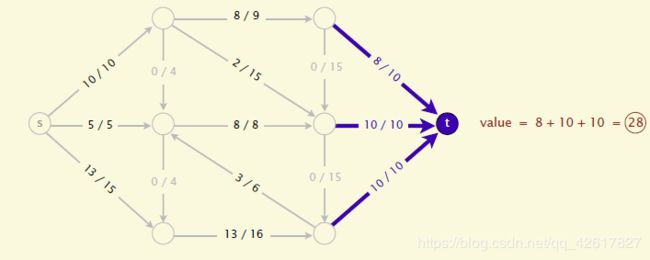
后面会发现Mincut和maxflow的问题是对偶的，解出了maxflow也就知道了mincut的解。再
介绍一种解maxflow的算法Ford-Fulkerson,为了方便，简称FF算法。
（1）初始化，所有边的flow都初始化为0

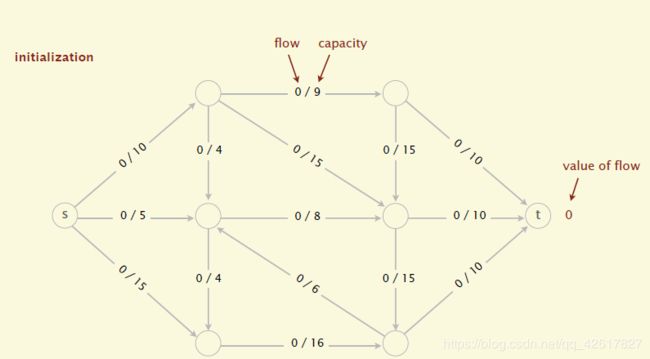
（2）沿着增广路径增加flow。增广路径是一条从s到t的无向路径，但也有些条件，可以经过没有满容量的前向路径（s到t）或者是不为空的反向路径(t->s)

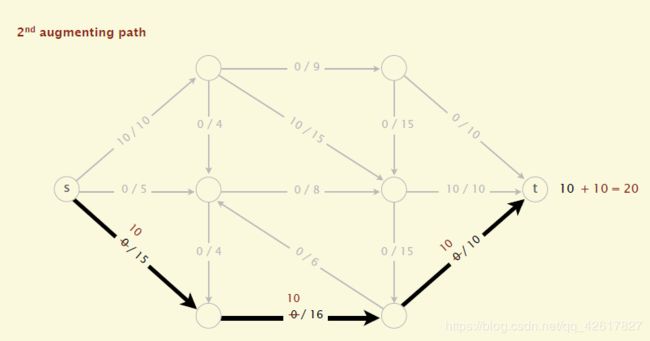
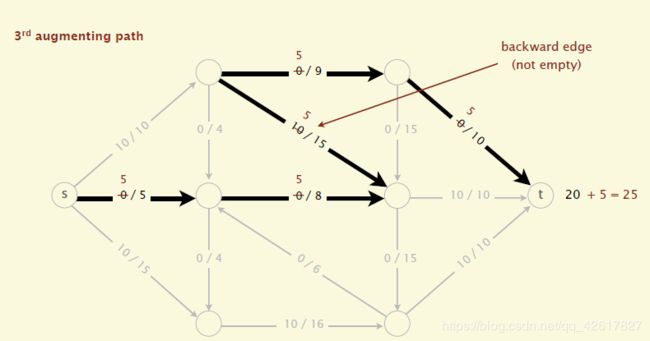
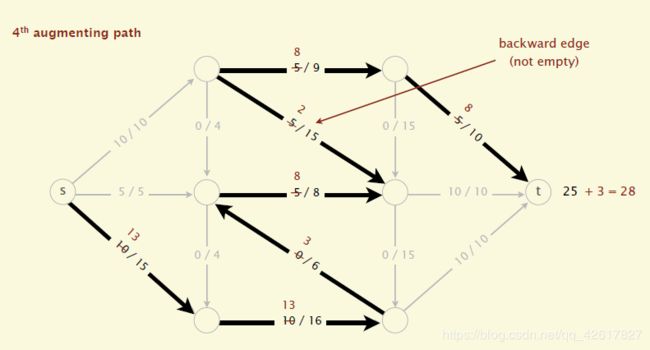
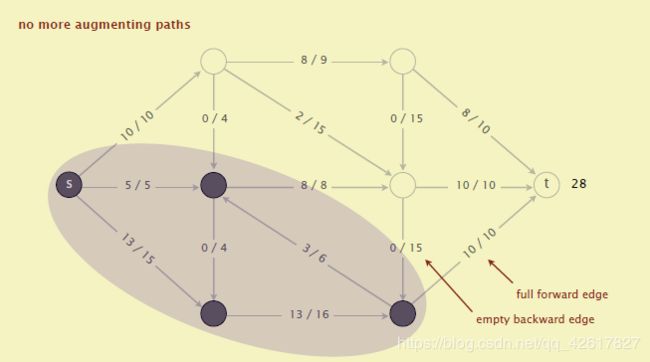
3 maxflow-mincut理论证明对偶性（optional）
首先定义一个概念net flow,经过一个割cut(A,B)的net flow等于从A到B的边flow的和减去从B到A边flow的和。
然后我们就有了flow-value引理：f为任意的流，(A,B)为任意的割，那么f的值 value of flow（也就是t的inflow）等于经过（A,B）的netflow.

如下图，value offlow = 8+9+10 = 27 , 而割的net flow = 8+2+7-2+12 = 27.

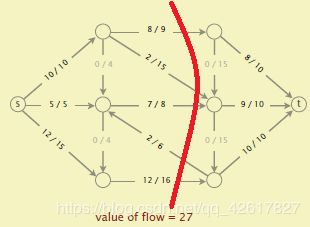
Weak duality(弱对偶)：f为任意的流，（A，B）为任意的割，那么Valueof flow <= capacity of cut(A,B)因为cut(A,B)等于从A到B流量，而value offlow等于cut（A，B）的netflow,还得减去从B到A边的流量。

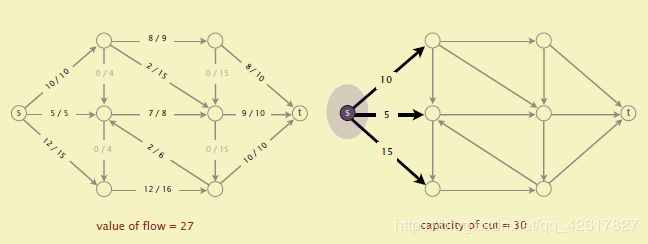
那么现在我们可以引出两个定理：增广路径定理（Augmenting Path theorem）:一个流f是最大流当且仅当没有增广路径。
最小割最大流定理（Maxflow-mincut theorem）:Maxflow的值等于最小割的容量。