深入浅出KNN算法

1. 概述

K最近邻(kNN，k-NearestNeighbor)分类算法

所谓K最近邻，就是k个最近的邻居的意思，说的是每个样本都可以用它最接近的k个邻居来代表。
kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也
属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的
类别来决定待分样本所属的类别。 kNN方法在类别决策时，只与极少量的相邻样本有关。由于kNN方法主要靠
周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，
因此对于类域的交叉或重叠较多的待分样本集来说，kNN方法较其他方法更为适合。

• 优点

1.简单，易于理解，易于实现，无需估计参数，无需训练；
2. 适合对稀有事件进行分类；
3.特别适合于多分类问题(multi-modal,对象具有多个类别标签)， kNN比SVM的表现要好。

• 缺点：

1.当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该
样本的K个邻居中大容量类的样本占多数。 该算法只计算“最近的”邻居样本，某一类的样本数量很大，那么或者
这类样本并不接近目标样本，或者这类样本很靠近目标样本。无论怎样，数量并不能影响运行结果。
2.该方法的另一个不足之处是计算量较大，因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能
求得它的K个最近邻点。
3.可理解性差，无法给出像决策树那样的规则。

2. Jupyter

• 情景

一直用的是pycharm，的确挺好用的，但是发现数据科学，AI更多项目是用的Jupyter，包括在飞桨上做项目，
所以还是记录一下怎么用吧。

• 安装
  anaconda自带的
• 更改默认浏览器
  因为个人喜欢用QQ浏览器，主要是之前存的书签都在哪儿了，在这里记录一下怎么更改浏览器

C:\Users\12521>jupyter notebook --generate-config  //生成配置文件
Writing default config to: C:\Users\12521\.jupyter\jupyter_notebook_config.py   
//按照提示的路径用文本编辑器将.py的配置文件打开

//搜索 c.NotebookApp.browser，然后照着下面的葫芦就能够成功的画出来葫芦，注意格式！

#c.NotebookApp.browser = ''
import webbrowser
webbrowser.register(
    "QQBrowser",  #自定义名字
    None, 
    webbrowser.GenericBrowser(u"F:\\Program Files\\Tencent\\QQBrowser\\QQBrowser.exe"))#指定浏览器所在位置
c.NotebookApp.browser = "QQBrowser" #名字

3. Jupyter的使用

• 这里有一篇讲的很好的文章
• 在这儿只抄录一些快捷键

A 会在活跃单元之上插入一个新的单元
B 会在活跃单元之下插入一个新单元。
连续按两次 D，可以删除一个单元。
撤销被删除的单元，按 Z。
Y 会将当前活跃的单元变成一个代码单元。
按住 Shift +上或下箭头可选择多个单元。在多选模式时，按住 Shift + M 可合并你的选择。
按 F 会弹出「查找和替换」菜单。

处于编辑模式时（在命令模式时按 Enter 会进入编辑模式），你会发现下列快捷键很有用：

Ctrl + Home 到达单元起始位置。
Ctrl + S 保存进度。
如之前提到的，Ctrl + Enter 会运行你的整个单元块。
Alt + Enter 不止会运行你的单元块，还会在下面添加一个新单元。
Ctrl + Shift + F 打开命令面板。

1 : 设定 1 级标题
2 : 设定 2 级标题
3 : 设定 3 级标题
4 : 设定 4 级标题
5 : 设定 5 级标题
6 : 设定 6 级标题
Y : 单元转入代码状态
M :单元转入markdown状态

4. 在Jupyter使用虚拟环境

• 目的
  为了让我的各个项目之间的编程环境干净一点，互不干扰，需要在Jupyter使用虚拟环境
  至于虚拟环境如何配置，在之前的一篇博客提到过
• 步骤

activate tf		//先得进入想要使用的虚拟环境，再进一步操作，不然就白搭，好多教程都没有提到这一点
conda install nb_conda

重启Jupyter，new中就出现了虚拟环境

5. 必要包的安装

• 进行操作需要安装一些包

conda install matplotlib,scikit-learn

• 包的简介
  • scikit-learn是一个非常牛批的开源的用于机器学习的Python模块
  • matplotlib是一个用于绘图的工具
    个人理解mat就是matrix（向量），plot是（绘图），lib是library（库）
    具体使用方法，准备最近抽时间基于绘制
    “I LOVE YOU”来分析和记录matplotlib的用法。

6. KNN算法的原理

• 分类问题

原理很简单，就是找靠近它的几个点的分类，这个点的类别就随大流儿。
KNN有一个参数叫**n_neighbors**,它设置的是找附近的几个点，如果点选少了就会使得分类不准确，但如果
多了的话就会使得算法的任务量大大增加，默认值选5个点。

• 回归问题

原理同样简单，找附近几个点的值，取这几个点的平均值作为预测点的值

7. KNN在分类任务中的用法

• 第一步：生成数据集

from sklearn.datasets import make_blobs					//导入生成数据的工具
from sklearn.neighbors import KNeighborsClassifier		//导入KNN分类器
import matplotlib.pyplot as plt							//导入matplotlib用于绘图
from sklearn.model_selection import train_test_split	//导入数据集拆分工具

data = make_blobs(n_samples=200,centers=2,random_state=8)	//为聚类产生数据集

X,y = data
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.spring,edgecolor='k')		//绘制散点图
plt.title("Use make_blobs generate two types of data sets")			//设置标题
plt.ylabel("Y 轴")					//添加轴标签
plt.xlabel("X 轴")		

plt.show()		//绘图命令

得到的分类数据集如下：

加餐0：

数据拆分工具的说明：
数据拆分工具的作用是把数据拆分为两大块，训练数据集和测试数据集。
其中，训练数据集用于模型的训练，而测试数据集用于测试我们训练出来的模型
两者占的比重默认是75%和25%

加餐1：

make_blob重要参数说明：
n_samples:表示数据样本点个数,默认值100
centers:产生数据的中心点，默认值3，也就是设置生成几撮数据
random_state:设置随机生成器的种子（此处涉及到随机数生成的算法。简单来说给定种子的意义在于，如果在
生成随机数的时候给定了种子，当下次再次生成随机数的时候，给定同一个种子，那么此次与上一次生成的随机
数是完全相同的）

make_blob参数说明：
n_features:表示数据的维度，默认值是2
cluster_std：数据集的标准差，浮点数或者浮点数序列，默认值1.0
center_box：中心确定之后的数据边界，默认值(-10.0, 10.0)
shuffle ：洗乱，默认值是True

加餐2：

对title的说明：
在此处如果你将标题设置为中文，那么程序会报错，加上这两行代码即可处理中文乱码
（事实上，用英文的title更专业一点）

plt.rcParams['font.sans-serif'] =['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False

加餐3：

X和y到底是什么？
测试代码如下：
np.shape(X)
>(200, 2)
>print（X）
array([[ 6.75445054,  9.74531933],
       [ 6.80526026, -0.2909292 ],
       ......
#我们发现，X是一个200*2的数组（我们设置的样本数为200，centers中心值是2,所以数据大体上是按照两个中
心各自分了100个点）

np.shape(y)
> (200,)
print(y)
> [0 1 0 1 0 0 1 0 0 1 1 1 0 0 1 1 0 0 1 0 0 1 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1
 1 1 0 0 1 1 0 1 0 0 0 1 0 1 1 0 1 1 1 0 1 0 0 1 0 1 0 1 0 1 0 0 0 0 0 1 0
 0 0 1 1 1 1 0 1 0 1 1 0 1 1 0 1 0 0 1 0 0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 1 0
 1 1 1 0 0 1 1 0 1 1 0 0 0 1 1 0 0 1 1 0 1 0 0 1 0 0 0 0 1 0 0 0 1 1 0 0 1
 0 1 1 1 0 0 0 1 0 0 0 1 1 1 1 1 0 0 0 1 0 0 0 1 1 1 1 1 0 0 0 0 1 0 0 0 1
 1 1 0 1 0 1 1 0 1 0 0 0 0 0 1]
 #我们发现，y是一个200*1的数组（我们设置的样本数为200）
 我们猜测这是计算机给数据的分类

加餐4：

plt.scatter用法？

• 第二步：分类

import numpy as np
clf = KNeighborsClassifier()		
clf.fit(X,y)						

x_min,x_max = X[:,0].min() - 1, X[:,0].max()+1			//设置最大和最小x值
y_min,y_max = X[:,1].min() - 1, X[:,1].max()+1			//设置最大和最小y值
xx,yy = np.meshgrid(np.arange(x_min,x_max,0.02),		//生成网格点坐标矩阵
                   np.arange(y_min,y_max,0.02))
z = clf.predict(np.c_[xx.ravel(),yy.ravel()])			//用训练数据拟合分类器模型
z = z.reshape(xx.shape)								//改变z的形状使得它与xx，yy的形状相同
plt.pcolormesh(xx,yy,z,cmap=plt.cm.Paired)
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.spring,edgecolor='k')
plt.xlim(xx.min(),xx.max())		//设置X轴的刻度范围
plt.ylim(yy.min(),yy.max())		//设置Y轴的刻度范围
plt.title("Classifier:KNN")
plt.show()

结果

加餐0：

对于x_min,x_max = X[:,0].min() - 1, X[:,0].max()+1，为什么最大值和最小值要减一和加一？？
我们要最大最小值的目的不是要真正意义上的最大值和最小值，实际上是为了设置x和y轴的刻度范围，刻度范围
比最值范围大一点图是更加美观的

加餐1：

np.meshgrid是干啥的？mesh 和 grid都是网格的意思（mesh也指电路中的网孔）
测试代码：
import numpy as np
import matplotlib.pyplot as plt
m,n = 5,3
x = np.linspace(0, 1, m)
y = np.linspace(0, 1, n)
X, Y = np.meshgrid(x,y)

print(x)
> [0.   0.25 0.5  0.75 1.  ]
print(y)
> [0.  0.5 1. ]

np.shape(X)
> (3, 5)
np.shape(Y)			//shape变得一样了，有点意思
> (3, 5)

print(X)
> [[0.   0.25 0.5  0.75 1.  ]
 [0.   0.25 0.5  0.75 1.  ]
 [0.   0.25 0.5  0.75 1.  ]]
print(Y)
> [[0.  0.  0.  0.  0. ]
 [0.5 0.5 0.5 0.5 0.5]
 [1.  1.  1.  1.  1. ]]				//从这个结果我们猜测，它做的类似广播机制，继续验证
 
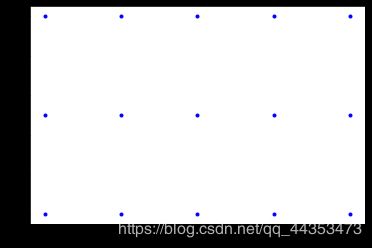
> plt.plot(X, Y, marker='.', color='blue', linestyle='none')
> plt.show()			//得到的图片如下

//事实证明，的确按照是这样
//所以对于此处的
xx,yy = np.meshgrid(np.arange(x_min,x_max,0.02),		
                   np.arange(y_min,y_max,0.02))
代码作用就是分别从x和y的取值范围中以0.02为步长生成两个数组，用这两个数组生成网格化的点数据

加餐2：

xx.ravel()？
ravel（）的作用是将矩阵扁平化变成向量
测试代码：
xx
> array([[ 3.33366829,  3.35366829,  3.37366829, ..., 10.97366829,
        10.99366829, 11.01366829],
        ........
xx.ravel()
> array([ 3.33366829,  3.35366829,  3.37366829, ..., 10.97366829,
       10.99366829, 11.01366829])		//所有的维都消失了        

加餐3：

np.c_和np.r_？？
简单来说
np.r_就是把两矩阵上下相加，要求列数相等；np.c_就是把两矩阵左右相加，要求行数相等。
一般来说，np.c_更加常用，因为很多时候需要将两个数组打包
实例：
import numpy as np
m=3
x = np.linspace(0, 1,m)
y = np.linspace(1,2,m)
np.c_[x,y]
> array([[0. , 1. ],
       [0.5, 1.5],
       [1. , 2. ]])

加餐4：

z是什么？是分类，此处用0和1来将数据分为两类
z = clf.predict(np.c_[xx.ravel(),yy.ravel()])
z
> array([1, 1, 1, ..., 0, 0, 0])
z = z.reshape(xx.shape)
> array([[1, 1, 1, ..., 1, 1, 1],
       [1, 1, 1, ..., 1, 1, 1],
       [1, 1, 1, ..., 1, 1, 1],
       ...,
       [0, 0, 0, ..., 0, 0, 0],
       [0, 0, 0, ..., 0, 0, 0],
       [0, 0, 0, ..., 0, 0, 0]])
验证代码：
print(clf.predict([[6.,9.]]))
plt.scatter(6.,9.,marker=".",color="blue",s=200)

[0]
//可以看出算法将点[6.0,9.0]分类分在了第一类
//如下图：

加餐5：

plt.scatter是啥？
matplotlib中绘制散点图的命令
matplotlib.pyplot.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=No
ne, vmax=None, alpha=None, linewidths=None, verts=None, edgecolors=None, *, data=None, **k
wargs)

重要参数说明：
x：一个(a,)维的数组
y：一个(b,)维的数组
s:是一个实数或者是一个(n,)维的数组，这个是一个可选的参数,表示的是绘图点的大小。
c:表示的是颜色，也是一个可选项。默认为蓝色“b”
marker:表示的是标记的样式，默认的是'o'。可以是常用的还有“ . ” 和 “ * ”
camp：cmap=plt.cm.spring是设置图标的样式
linewidths:标记点的长度

8. KNN处理多元分类任务

• 第一步，生成数据

from sklearn.datasets import make_blobs
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import numpy as np

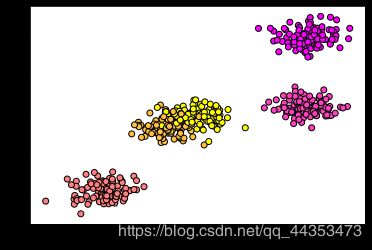
data = make_blobs(n_samples=500,centers=5,random_state=8)
X,Y = data
plt.scatter(X[:,0],X[:,1],c=Y,cmap=plt.cm.spring,edgecolor='k')
plt.show()

生成的数据图片如下：

• 第二步，分类：

t1 = time.time()
clf = KNeighborsClassifier()
clf.fit(X,Y)
x_min,x_max = X[:,0].min() - 1, X[:,0].max()+1
y_min,y_max = X[:,1].min() - 1, X[:,1].max()+1
xx,yy = np.meshgrid(np.arange(x_min,x_max,0.02),
                   np.arange(y_min,y_max,0.02))
z = clf.predict(np.c_[xx.ravel(),yy.ravel()])
z = z.reshape(xx.shape)
plt.pcolormesh(xx,yy,z,cmap=plt.cm.Paired)
plt.scatter(X[:,0],X[:,1],c=Y,cmap=plt.cm.spring,edgecolor='k')
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.title("Classifier:KNN")
plt.show()
t2 = time.time()
print("此次分类用了%s秒"%(t2-t1))
												#可以说，程序整体与二分类完全没有区别

得到结果如下：

此次分类用了50.0981240272522秒
//用了很长的一段时间呐

• 第三步，模型测试

//模型训练出来了，到底怎么样，是骡子是马，拉出去溜溜就知道了
score = clf.score(X,Y)
print("模型正确率为：%s"%score)
模型正确率为：0.955					//正确率还是挺高的

9. KNN用于回归问题

• 第一步，生成数据集

from sklearn.datasets import make_regression
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import numpy as np

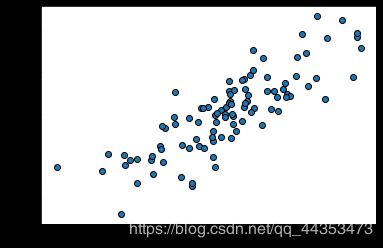
X,Y=make_regression(n_features=1,n_informative=1,noise=50,random_state=8)
plt.scatter(X,Y,edgecolor="k")
plt.show()

生成数据图片如下：

加餐0：

make_regression重要参数：
n_samples：样本数量，默认为100。
n_features：对应每个样本的特征的数量，默认100（默认值有点多啊。）
n_informative：可选(默认值=10)信息特征的数量，即用于构建用于生成输出的线性模型的特征数。
random_state：如前文所讲

• 第二步，拟合：

from sklearn.neighbors import KNeighborsRegressor
reg = KNeighborsRegressor()

reg.fit(X,Y)
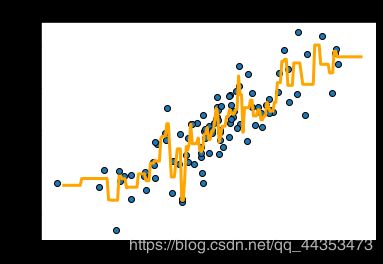
z = np.linspace(-3,3,200).reshape(-1,1)				//变形
plt.scatter(X,Y,edgecolor="k")						//绘点
plt.plot(z,reg.predict(z),c="orange",linewidth=3)	//画线
plt.title('KNN Regression')
plt.show()

结果如下：

加餐0：

z = np.linspace(-3,3,200).reshape(-1,1)，z是个毛？
是从-3到3中取200个点，生成一个向量后再reshape

问题来了，reshape又是干什么的？
//上代码
import numpy as np
> a = np.linspace(1,9,9)
array([1., 2., 3., 4., 5., 6., 7., 8., 9.])
> a.reshape(3,3)
array([[1., 2., 3.],
       [4., 5., 6.],
       [7., 8., 9.]])
							//前面的看起来很好理解，改变形状吗，那就来点不一样的
> b = a.reshape(3,3)
> b.reshape(-1)
array([1., 2., 3., 4., 5., 6., 7., 8., 9.])
> b.reshape(-1,1)					//简单的分析：
array([[1.],						//一共有9个数字，给出第二个数字为1，那么reshape自动
										计算出维度应该是9*1并变形
       [2.],
       [3.],
       [4.],
       [5.],
       [6.],
       [7.],
       [8.],
       [9.]])
> b.reshape(-1,3)					//再次验证
array([[1., 2., 3.],				//给出第二个维度是3，reshape自动计算出维度是3*3，并变形
       [4., 5., 6.],
       [7., 8., 9.]])

//所以，对于此处reshape的作用就是把z变成一个200*1的数组

• 第三步，对模型打分

score = reg.score(X,Y)
print("模型正确率为：%s"%score)
模型正确率为：0.7721167832505298			//相对与分类来说，这次回归模型的表现不够好

• 第四步，改进

//关于KNN算法，在一开始提到过，根据邻近点来判断预测自己的值，默认我们是选五个邻近点的，我们尝试
少选几个点
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt
import numpy as np

X,Y=make_regression(n_features=1,n_informative=1,noise=50,random_state=8)
from sklearn.neighbors import KNeighborsRegressor
reg = KNeighborsRegressor(n_neighbors=2)				//改动
reg.fit(X,Y)
z = np.linspace(-3,3,200).reshape(-1,1)
plt.scatter(X,Y,edgecolor="k")
plt.plot(z,reg.predict(z),c="orange",linewidth=3)
plt.title('KNN Regression')
plt.show()
score = reg.score(X,Y)
print("模型正确率为：%s"%score)

结果：
模型正确率为：0.8581798802065704

模型的正确率的确提高了，但是这就真的是好事儿吗，不见得，以后会进一步讨论。

10. Question

通过上面的几次应用，我们发现，用scikit-learn库不是一件难事儿，我们要做的就是处理好数据，剩下的就
交给库处理就好了，我们并没有真正的接触到算法呐，这就是scikit-learn库与tensorflow 的区别。
scikit-learn库易用，但是主要用在中小型的项目中，tensorflow灵活性好，主要用于大型的项目。用ten
sorflow算法是要自己编的，这样更加能接触到本质，使用scikit-learn库更多的像是在调用方法（这与
keras挺像的）。
饭要一口一口的吃，学习scikit-learn库还是非常有意义的，它让你对深度学习过程有个不错的了解，这就为
你以后学习tensorflow或者配合tensorflow使用，或者是直接应用都有良多的好处的。

11. KNN实战–酒的分类

• 背景

在此之前我们的都是先用计算机随机生成数据集之后再进行分类或者回归操作，我们的模型拟合的不错，计算机
的确是靠自己的算法拟合出来的各种模型，但是这似乎还并不是那么具有说服力，一是比较简单二是不够贴近现
实，让我们用真实的数据模拟一回。

• 分析

> from sklearn.datasets import load_wine			//导入数据
> import matplotlib.pyplot as plt
> import numpy as np

> wine = load_wine()

> wine.keys()					//看看这个数据集的keys有哪些
dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names'])
> wine.data.shape				//数据集的维度是178*13
(178, 13)
> wine.data						//数据集大致长这样子
"""array([[1.423e+01, 1.710e+00, 2.430e+00, ..., 1.040e+00, 3.920e+00,
        1.065e+03],
       [1.320e+01, 1.780e+00, 2.140e+00, ..., 1.050e+00, 3.400e+00,
        1.050e+03],"""
        ..........

> from sklearn.model_selection import train_test_split
X,x,Y,y = train_test_split(						//X用于训练，x用于测试，Y用于训练，y用于测试
wine.data,wine.target,random_state=0)			//分成训练和测试数据集
> X.shape										
(133, 13)
> x.shape										//看看train_test_split是如何分的？大概是3：1
(45, 13)
> Y.shape
(133,)
> y.shape
(45,)

> from sklearn.neighbors import KNeighborsClassifier
> clf = KNeighborsClassifier(n_neighbors=1)		//n_neighbors=1
> clf.fit(X,Y)									//拟合

> wine.data[1]									//第一个数据的features
array([1.32e+01, 1.78e+00, 2.14e+00, 1.12e+01, 1.00e+02, 2.65e+00,
       2.76e+00, 2.60e-01, 1.28e+00, 4.38e+00, 1.05e+00, 3.40e+00,
       1.05e+03])
> clf.predict([wine.data[1]])			//把第一个数据features放入到模型中看模型给出的分类结果
array([0])								//模型把它分到了第一类
> wine.target[1]						//验证一下，的确是在第一类，看来我们的模型不错
0

> score = clf.score(x,y)						//打分
> score
0.7555555555555555								//马马虎虎

加餐0：

导入的是什么？是sklearn自带的一个红酒数据集
通过print(wine.DESCR)可以看看它的介绍(截取一部分)

.. _wine_dataset:

Wine recognition dataset
------------------------

**Data Set Characteristics:**

    :Number of Instances: 178 (50 in each of three classes)					//一共有178个样本
    :Number of Attributes: 13 numeric, predictive attributes and the class	//每个样本有13个属性
    :Attribute Information:
 		- Alcohol
 		- Malic acid
 		- Ash
		- Alcalinity of ash  
 		- Magnesium
		- Total phenols
 		- Flavanoids
 		- Nonflavanoid phenols
 		- Proanthocyanins
		- Color intensity
 		- Hue
 		- OD280/OD315 of diluted wines
 		- Proline

    - class:								//数据将这178个样本分成了三类
            - class_0
            - class_1
            - class_2
    .			...........................

加餐1：

此处因为我们的特征比较多，所以难将数据以图的形式表现出来，但是我们还是通过打分验证出我们的模型还是
不错的。

12. 总结

在这篇博客中，详细的介绍了KNN的用法并进行了实战。
在使用的过程中我们发现了它的特点：
第一，简单易用
第二，需要对数据集认真地进行预处理，sklearn几乎都无法避免
第三，规模大的数据集拟合的时间较长，在实践中，我们仅仅用了500个样本就耗时良多，更别提大 规模的数据集了
第四，对高维数据集拟合欠佳。我们看到在面对低维度的数据集的时候，模型表现不错，可以达到96%左右的正确率，但是当面对高维度的数据时，即使我们把n_neighbors设置为1（事实上这就有点不科学了），模型的正确率才仅仅在76%左右。

接下来,我们会开始学习同样经典,而且在高维数据集中表现良好的算法广义
线性模型。

>>> import time
>>> time.ctime()
'Fri Sep  6 17:36:50 2019'			//博客完成时间