2020牛客暑期多校训练营（第一场）

I 1 or 2

题意：一个图有n个点，m条边，边的表示方法是用n个点中的两个。这n个点都有一个要求，就是需要有 $di$ 条边经过自己。然后给你这n个点的要求，还有m条野生的边，让你任意选若干条，满足每一个点的要求，可以的话输出Yes，不行就No。

思路： 注：并不是正解。 这个题目最后一句好难读。读懂之后觉得是个最大流问题，奈何刷的太少，图建不出来。一开始这么想：每个点都有一个需求量，我们可以搞一个超级源点来发射这些需求，然后用一个超级汇点来接收流过来的最大需求量，然后比较一下，源点发出的和汇点接收的一样的话就是ok的，不一样就证明需求量有损失，边的个数是不够的。有这个思路就可以 建图 之后用 最大流 来解决。

以第三个样例说明一下

我一开始建的图：

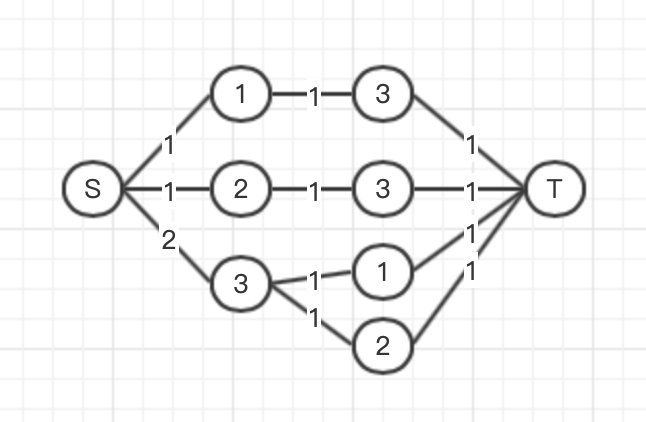
随便来了一把这个图建出来之后感觉妙极了，根本不晓得完全错了。这个图只能筛选掉边数不够的情况，因为这个图会把所有的边都接上来，如果有的节点经过的边不能满足需求，那么从他那里出来的边的个数就不够需求量，到达汇点的量自然就不够数，所以这个图没有考虑到那种边给的超级多，超出了你的需求量的那种，我这个流过去也是可以前后相等的，所以不行。

那有个什么办法可以限制一这种超过需求量的情况呢？可以用和源点相同的办法，你源点发出的需求量是根据每个点分配的，那么我汇点接收也要落实到每个点。这个时候就要用一下最大流的常用手段（应该是的吧），把一个点分成两个用，分割的点就用来连接汇点和之前跟自己连接的原来本身的点，这样每一个点的流量就可以框起来了。文字有一点抽象，上图：

中间的流量都是1。

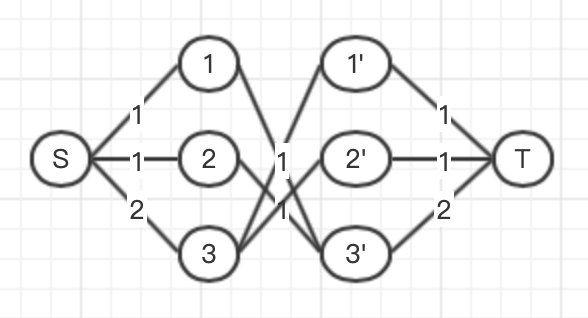
图都建好了，这个题也就是上模版了。

#include
#define INF 0x3f3f3f3f
using namespace std;
struct EDGE {
	int to, w, next;
} edge[2000];
int cnt;
int head[2000];
int deep[2000];

void init() {
	cnt = 0;
	memset(head, -1, sizeof(head));
}

void addedge(int u, int v, int w) {
	edge[cnt].to=v; edge[cnt].w=w; edge[cnt].next=head[u]; head[u]=cnt++;
	edge[cnt].to=u; edge[cnt].w=0; edge[cnt].next=head[v]; head[v]=cnt++;
}

int bfs(int s, int t) {
	queue<int> q;
	memset(deep, 0, sizeof(deep));
	q.push(s);
	deep[s] = 1;
	int top;
	while(!q.empty()) {
		top = q.front();
		q.pop();
		for(int i = head[top];i+1; i = edge[i].next) {
			int v = edge[i].to;
			int w = edge[i].w;
			if(!deep[v]&&w) {
				deep[v] = deep[top]+1;
				q.push(v);
			}
		}
	}
	return deep[t];
}

int dfs(int s, int t, int inflow) {
	if(s==t) return inflow;
	int acflow=0;
	for(int i=head[s]; i+1; i=edge[i].next) {
		if(edge[i].w && deep[s]+1 == deep[edge[i].to]) {
			int x = dfs(edge[i].to,t,min(inflow, edge[i].w));
			if(x>0) {
				acflow+=x; inflow-=x;edge[i].w -= x; edge[i^1].w += x;
				if(!inflow) break;
			}
		}
	}
	if(!acflow) deep[s] = -2;
	return acflow;
}

int dinic(int s,int t) {
	int f = 0;
	while(bfs(s,t)) f += dfs(s,t,INF);
	return f;
}

int n, m, a, b;
int d[55];

int main() {
	while(~scanf("%d %d", &n, &m)) {
		init();
		int sum = 0;
		for(int i = 1;i <= n; i++) {
			scanf("%d", &d[i]);
			sum += d[i];
			addedge(0, i, d[i]);
		}
		
		int l = 1e9, r = 0;
		for(int i = 1;i <= m; i++) {
			scanf("%d %d", &a, &b);
			addedge(a, b+n, 1);
			l = min(l, b+n); r = max(r, b+n);
			addedge(b, a+n, 1);
			l = min(l, a+n); r = max(r, a+n);
		}
		
		int fin = r+1;
		for(int i = l;i <= r; i++) {
			addedge(i, fin, d[i-n]);
		}
		
		printf("%s\n", dinic(0, fin)==sum?"Yes":"No");
	}
}