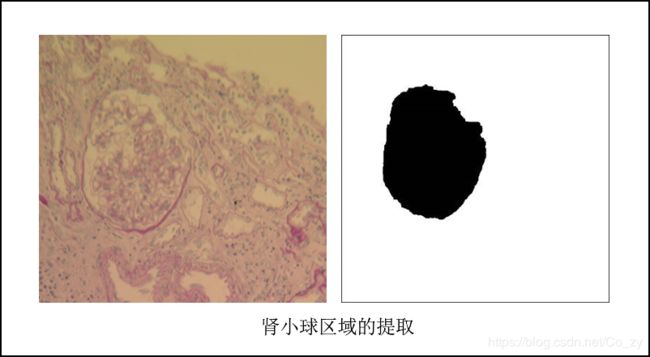
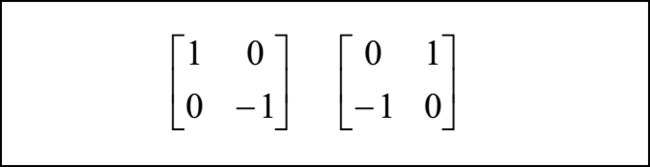图像处理与分析 && 计算机视觉 && 医学图像

第一部分是图像处理与分析,第一部分部分是计算机视觉,第三部分是医学图像.

《第一部分》

一、第一次课

1.1 读取bmp图片

参考

简单bmp图片处理工具——python实现
https://www.cnblogs.com/zyp4614/p/6917943.html
Python Struct读取bmp图片信息
https://blog.csdn.net/zoujin6649/article/details/81357696
Python中struct.pack()和struct.unpack()用法详细说明
https://blog.csdn.net/weiwangchao_/article/details/80395941

Python版

from struct import unpack

with open('./bmp_19201080.bmp','rb') as f:
    s = f.read(30)

print(unpack(', s))
'''
(b'B', b'M', 6220854, 0, 54, 40, 1920, 1080, 1, 24)
b'B、b'M说明是Windows位图
一个4字节整数：位图大小
一个4字节整数：保留位，始终为0
一个4字节整数：实际图像的偏移量
一个4字节整数：Header的字节数
一个4字节整数：图像宽度
一个4字节整数：图像高度
一个2字节整数：始终为1
一个2字节整数：颜色数
'''

def bmp_info():
    unpackbuf = unpack(',s)
    if (unpackbuf[0]!=b'B' or unpackbuf[1]!=b'M'):
        return None
    else:
        return {'width':unpackbuf[6],'height':unpackbuf[7],'color':unpackbuf[9]}
bi = bmp_info()

print(bi['width'],'*',bi['height'],bi['color'])

C版

#include "stdafx.h"
#include "ImgAlg.h"
#include  
#include  //printf for linux
#include  //abs for linux
#include  //memset for linux

#define PI 3.141592653589
int Load8bitBmp(const char* FileName,BYTE* img,int& width,int& height)
{
    FILE* fp=fopen(FileName,"rb");
    if(fp==NULL)
    {Message("open file error"); return 0;}

    BITMAPFILEHEADER  FileHeader;
    if( fread(&FileHeader,sizeof(BITMAPFILEHEADER),1,fp)!=1 )
    {Message("read file error"); return 0;}
    if( FileHeader.bfType != 0x4d42 )
    {Message("no bmp file format"); return 0;}
    
    BITMAPINFOHEADER InfoHeader;
    if( fread(&InfoHeader,sizeof(BITMAPINFOHEADER),1,fp)!=1 )
    {Message("read file error"); return 0;}
    if(InfoHeader.biBitCount != 8)
    {Message("no 8 bit bmp file"); return 0;}
    if(InfoHeader.biCompression != 0)
    {Message("compression mode"); return 0;}
    width = InfoHeader.biWidth  ;
    height= InfoHeader.biHeight ;

    fseek(fp,FileHeader.bfOffBits ,SEEK_SET);
    for(int i=height-1;i>=0 ;i--)
    {
        if( fread(img+i*width,width,1,fp)!= 1 )
        {Message("read file error"); return 0;}         
        if(width%4!=0)
        fseek(fp,4-width%4,SEEK_CUR);
    }
    
    fclose(fp);
    return 1;
}

二、 第二次课

2. 1 dpi(dot per inch)计算

(1) dpi(dot per inch)计算

(2$\times$ 1200 + 4 $\times$ 1200)$\times$ 3
解释:1200dpi意思是每英寸可采集1200个像素点,现在照片横向2英寸,纵向4英寸,所以总共是(2$\times$ 1200 + 4 $\times$ 1200), 然后24位彩色,1像素 = 3 bytes.

(2) 扫描完后 如果用600dpi打印出来,问打印出来的照片尺寸?(不缩放)
2400 / 600 = 4
4800 / 600 = 8

2.2 灰度直方图（histogram）

2.2.1 定义

灰度直方图（histogram）是灰度级的函数，是图象的最基本的统计特征。它表示图象中有每种灰度级的象素的个数，反映图象中每种灰度出现的频率。如下图所示，
横坐标：灰度－r , 纵坐标：为某一灰度值ri的像素个数ni,或是灰度出现的概率P( r)

从概率的观点来理解，灰度出现的频率可看作其出现的概率，这样直方图就对应于概率密度函数pdf(probability density function)，而概率分布函数就是直方图的累积和，即概率密度函数的积分，如下图所示：

2.2.2 编程实现灰度直方图

方法一:逐个点扫描

unsigned long hist[256];
unsigned char *pCur;
for(int i=0;i<256;i++) 
	hist[i]=0;
	
for(i=0;i<height;i++)	
	for(j=0;j<width;j++)
		hist[pImg + i*width + j]++;

方法二:效率高 (考试)

unsigned long hist[256];
unsigned char *pCur;
for(int i=0;i<256;i++) 
	hist[i]=0;
int ImgSize=width*height;
for(i=0,pCur=pImg;i<ImgSize;i++) 
	hist[*(pCur++)]++;

拓展参考

十一.灰度直方图概念及OpenCV绘制直方图
https://blog.csdn.net/eastmount/article/details/83758402

2.3 灰度变换(均衡化)

2.4 二值化???

OpenCV—图像二值化
https://www.cnblogs.com/ssyfj/p/9272615.html#%E4%B8%89opencv%E4%B8%AD%E7%9A%84%E4%BA%8C%E5%80%BC%E5%8C%96%E6%96%B9%E6%B3%95

python实现直方图均衡化(HE)
https://blog.csdn.net/qq_30967115/article/details/85210870

import cv2  # 利用opencv读取图像
import numpy as np
# 利用matplotlib显示图像
import matplotlib.pyplot as plt 

img = cv2.imread("C:/Users/asus/Pictures/Victoria.jpg") #读取图像
img = img[:,:,(2,1,0)]
r,g,b = [img[:,:,i] for i in range(3)]
img_gray = r*0.299+g*0.587+b*0.114


img_gray_1D = img_gray.flatten()
_,_,_ = plt.hist(img_gray_1D,bins=256,normed=0)
# plt.show()


img_gray_1D = img_gray.flatten()
img_gray_1D_len = img_gray_1D.shape[0]
img_gray_1D_int = (img_gray_1D + 0.5).astype(np.uint8)

Psk = np.zeros(256)

for i in range(img_gray_1D.shape[0]):
    Psk[(img_gray_1D_int[i])] += 1
Psk = [Psk[i] / img_gray_1D_len for i in range(256)]

cdf = np.zeros(256)
cdf[0] = Psk[0]
for i in range(255):
    cdf[i + 1] = cdf[i] + Psk[i + 1]

#计算目标像素 并将一维向量还原成二维的灰度图
img_gray_1D_re = np.array([255 * cdf[img_gray_1D_int[i]] for i in range(len(img_gray_1D))])
img_re = img_gray_1D_re.reshape((img_gray_1D_len,-1))


# 显示图像
# plt.imshow(img_re,cmap="gray")
# plt.axis('off')
# plt.show()
img_gray_1D = img_gray.flatten()
_,_,_ = plt.hist(img_gray_1D_re,bins=256,normed=0)
plt.show()

三、 第三次课

3.1 点运算

由于点运算在处理与显示中的重要性，图象处理系统都有专门的处理硬件与之对应，以便能够以视频速率实时完成操作，这样的部件称为查找表LUT(LookUpTable)。通常图象处理系统都有成组的查找表供编程使用
在通用的计算机上，没有查找表可以直接利用，通过软件逐点处理来实现，这时查找表仅表现为一种数据结构。因为在数字图像处理中，自变量g的值域是有限的，比如通常的灰度图像中，0<=g<=255，最多只有256种取值，因此，对于实现任意的G=F(g)而言，都可以使用查表的方法实现
方法一: 慢

for( i = 0,pCur=pImg; i < Imgsize; i ++) 
	*(pCur++) = F(*pCur);

要计算ImgSize次，当图像为512x512时，F要被计算262144次

方法二: 快 (考试)

BYTE LUT[256];
BYTE *pCur,
for(g = 0;g < 256;g++) 
	LUT[g ] = F(g);
	*pEnd = pImg + ImgSize;
for(pCur = pImg; pCur < pEnd;pCur++) 
	*(pCur++) = LUT[*pCur];

在使用LUT时，F函数仅被计算256次。

3.2 代数运算

3.2.1 加法运算

图象相加一般用于对同一场景的多幅图象求平均，以便有效地降低加性（additive）随机噪声。通常图象采集系统中采集图象时有这样的参数可供选择。通常直接采集的图象品质较好，不需要这样的处理，但是对于经过长距离模拟通讯方式传送的图象（如太空航天器传回的星际图象）这种处理是不可缺少的。利用求平均的方法降低噪声信号提高信噪比的做法，只有当噪声可以用同一个独立分布的随机模型描述时才会有效

3.2.2 减法运算

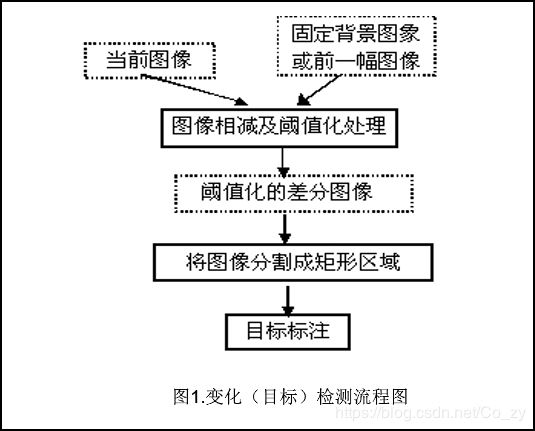
图象相减是常用的图象处理方法，用于检测变化及运动物体。在可控制的条件下，如工业视觉环境下，这种称之为差分方法的简单处理与阈值化处理一道往往是建立机器视觉系统最有效的方法之一。在相对稳定的环境下，可以假设背景变化缓慢，且符合一定的分布规律，通过建立背景模型，实施差分方法来检测运动物体，可以获得很好的效果。因此，差分方法可以分为控制环境下的简单差分方法和基于背景模型的差分方法。


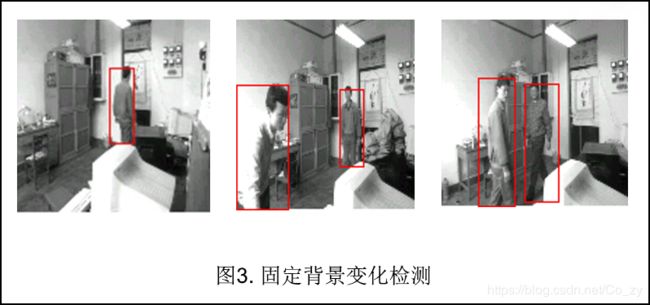
在控制环境下，或者在很短的时间间隔内，可以认为背景是固定不变的，可以直接使用差分方法检测变化或直接分割出作为前景的物体。其流程图如下：

作业
1.编制将两个灰度图象相减的程序，注意合理处理数值区间，以便显示差图象，例如取绝对值或适当平移等（输入输出图象格式bmp）。
2.编制将一灰度图象与将其少许平移后得到的图象相减的程序，观察其效果。

3.3 几何运算

几何运算与点运算不同，它可改变图象中物体（象素）之间的空间关系。这种运算可以看成将各象素在图象内移动的过程。其定义为：g(x,y)=f(x’,y’)=f[a(x,y),b(x,y)] ，其中，f(x,y)表示输入图象，g(x,y)表示输出图象，a(x,y)和b(x,y)表示空间变换，若它们是连续的，则将保持图象中的连通关系。

3.3.1 实现几何运算有两种方法

• 其一为前向映射法，即：将输入象素的灰度一个个地转移到输出图象中，如果一个输入象素被映射到四个输出象素之间的位置，则其灰度值就按插值法在四个输出象素之间进行分配；
  
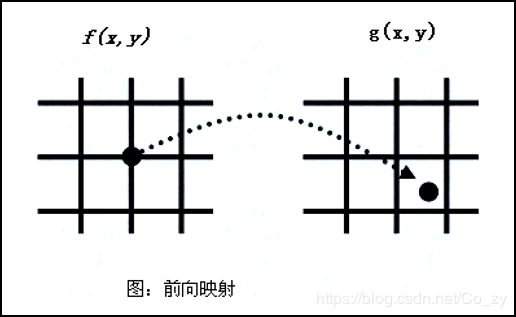
• 其二为后向映射法（象素填充法），这时将输出象素逐个地映射回输入图象中，若输出象素被映射到四个输入象素之间的位置，则其灰度由它们的插值来确定。在实际中，通常采用后向映射法。
  
  图像旋转后,会出现许多空洞点,我们需要对这些空洞点必须进行填充处理,否则图像旋转后的效果不好,一般也称这种操作为插值处理,最简单的插值方法是最近邻插值，即选择离它所映射到的位置最近的输入象素的灰度值为插值结果。复杂一点的方法是双线性插值,如下图所示:
  

3.3.2 仿射变换

其中 A 是变形矩阵，b是平移矢量。在2维空间，A可以按如下的四个步骤分解：尺度、伸缩、扭曲、旋转

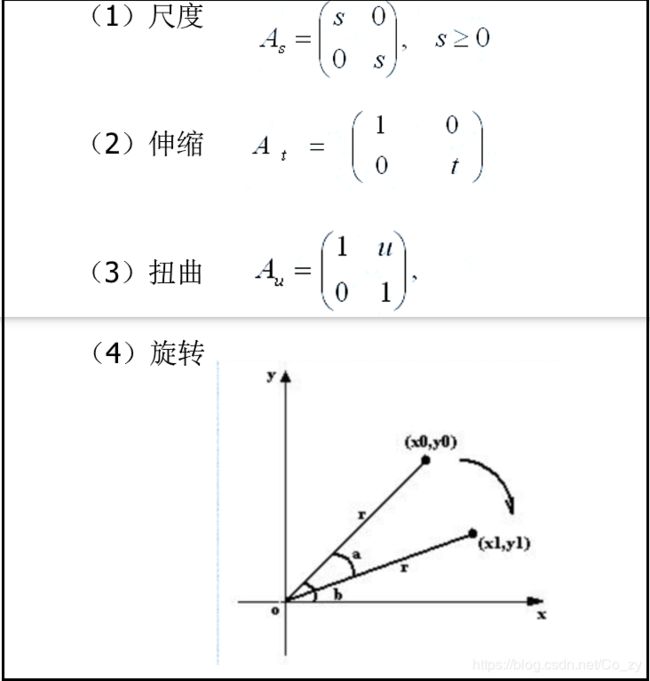
将一个点顺时针旋转a角，r为该点到原点的距离，在旋转过程中，r保持不变；b为r与x轴之间的夹角。
旋转前：x0=rcosb；y0=rsinb
旋转a角度后：
x1 = rcos(b-a) = rcosbcosa + rsinbsina = x0cosa + y0sina；
y1 = rsin(b-a) = rsinbcosa - rcosbsina = -x0sina + y0cosa；

3.3.3 透视变换(Perspective Transformation)

透视变换是中心投影的射影变换，在用非齐次射影坐标表达时是平面的分式线性变换，具有如下的形式：

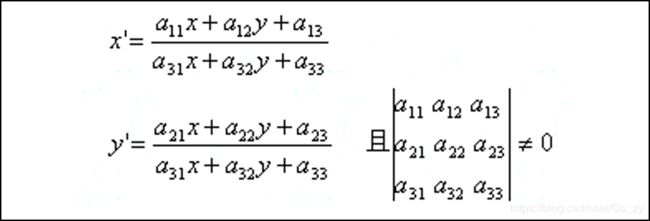
透视变换常用于图象的校正，例如在移动机器人视觉导航研究中，由于摄象机与地面之间有一倾斜角，而不是直接垂直朝下（正投影），有时希望将图象校正成正投影的形式，就需要利用透视变换。
下面看一个案例
在地面上取定一个矩形（不一定是正方形），要求它的边平行或垂直于车体轴线，这样的矩形在原始图象中显示为一个等腰梯形，如图所示。

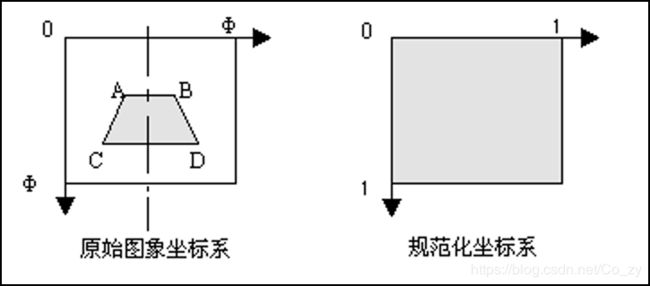
设A点的坐标为（x1,y1），C点坐标为(x2,y2)，则B、D的坐标分别是（φ-x1,y1）和(φ-x2,y2)。经过投影，ABCD四个点依此与规范化坐标系中的(0,0),(1,0),(0,1),(1,1)四个点相对应。把此对应关系代入上式，得
略

---

作业
1 完成图像的双线性差值旋转的程序。
2 编制实现透视及仿射变换的程序，通过交互 输入参数观察效果。

---

3.4 邻域运算

模板：模板就是一个矩阵（其实就是下面说的卷积核），也就是处理图像这个过程对应的函数，对应卷积运算。
卷积运算：可以看做加权求和的过程，为了图像增强和减少噪声，用该像素点的邻域像素点进行加权，得到处理完之后这个点的像素点（会把噪声减弱，当然也会有别的问题）。
卷积核：上面不是说了卷积运算了嘛，这个点的邻域和哪个矩阵进行加权啊？换句话说，这个点的邻域那么多像素点，这些像素点所占的权重是多少啊？这些权重构成一个矩阵，这个矩阵就叫卷积核，卷积核的行数和列数都是奇数。
————————————————
版权声明：本文为CSDN博主「lixin051435」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/tsfx051435adsl/article/details/78305643

四、图像平滑

4.1 图像噪声

图像噪声产生的原因很复杂，有的可能是数字信号在传输过程中发生了丢失或者受到干扰，有的是成像设备或者环境本身导致成像质量不稳定，反应到图像上就是图像的亮度与颜色呈现某种程度的不一致性。

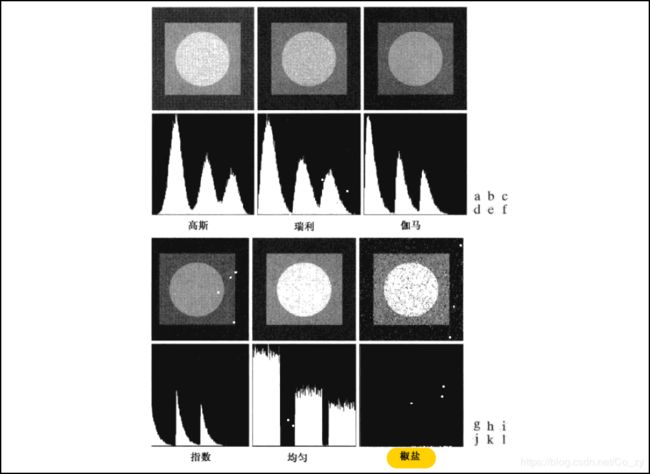
从噪声的类型上，常见的图像噪声分为以下几种：

• 高斯噪声/符合高斯分布
  一般会在数码相机的图像采集（acquisition）阶段发生，这时它的物理、电、光等各种信号都可能导致产生高斯分布噪声。
• 均匀分布噪声(实际不常见,模拟常用)
  均匀/规则噪声一般都是因为某些规律性的错误导致的。
• 椒盐噪声(脉冲噪声) 黑白的点
  是一种随机在图像中出现的稀疏分布的黑白像素点， 对椒盐噪声一种有效的去噪手段就是图像中值滤波。
  

————————————————
版权声明：本文为CSDN博主「kingkee」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/kingkee/article/details/93617051

4.2 图像平滑

图像平滑从信号处理的角度看就是去除其中的高频信息，保留低频信息。因此我们可以对图像实施低通滤波。低通滤波可以去除图像中的噪音，模糊图像(噪音是图像中变化比较大的区域，也就是高频信息)。而高通滤波能够提取图像的边缘(边缘也是高频信息集中的区域)。

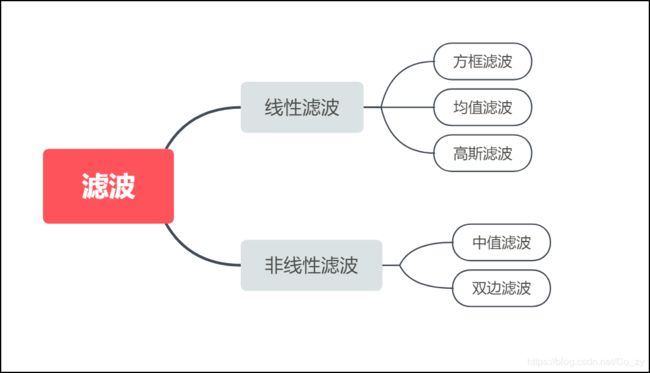
根据滤波器的不同又可以分为均值滤波，高斯加权滤波，中值滤波， 双边滤波。
( 参考 【数字图像处理】 图像平滑 )

▲ 图像处理的几种滤波(含核的解释)

边缘检测

边缘是指其周围象素的灰度有阶跃变化(step edge)或屋顶状变化(roof edge)的象素、常存在于目标与背景之间、目标与目标之间、目标与其影子之间。
分析手段：因为灰度的变化，可以反映为导数；因此，根据边缘的形状，可以通过求导的方法来寻求边缘。边缘的参数包括：边缘强度(edge intensity)和边缘方向(edge direction)。

下面具体展开:

• Roberts算子
  定义为：G(i ,j)=|f(i,j)-f(i+1,j+1)|+|f(i+1,j)-f(i,j+1)|
  
• Prewitt算子
  
• Sobel算子
  

---

(滤波和边缘检测可以结合起来)
然后去读这篇博客:

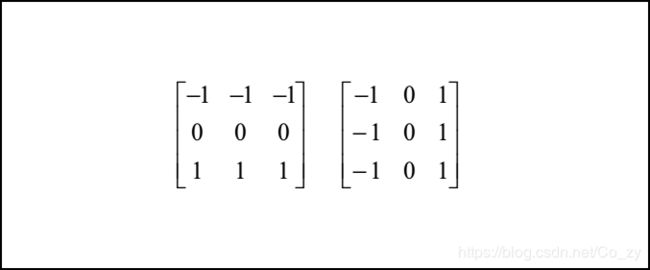
▲ 彻底理解数字图像处理中的卷积-以Sobel算子为例

▲ 卷积计算动图

图像分割

图象分割是将图象划分为若干互不相交的小区域的过程。小区域是某种意义下具有共同属性的象素的连通集合，如物体所占的图象区域、天空区域、草地等。
图像分割的目的:

• 图像分割使得画面场景被分为“目标物”及“非目标物”两类,即将图像的像素变换为黑、白两种。
• 因为结果图像为二值图像，所以通常又称图像分割为图像的二值化处理。

阈值是在分割时作为区分物体与背景象素的门限，大于或等于阈值的象素属于物体，而其它属于背景。这种方法对于在物体与背景之间存在明显差别（对比）的景物分割十分有效。实际上，在任何实际应用的图象处理系统中，都要用到阈值化技术。为了有效地分割物体与背景，人们发展了各种各样的阈值处理技术，包括全局阈值、自适应阈值、最佳阈值等等。

• p率阈值化
  一般用于灰度图像，使用条件是已知目标在政府图像中所占的面积比为P%(需要先验知识)，先得到图像的灰度直方图，然后从小到大累加，直到为P%，记录当前灰度，以它为阈值来分割图像。条件很苛刻，大部分情况下都用不上。

• 基于类间方差的阈值分割法

• 基于熵的阈值选取（Entropy）

• 循环迭代策略得到阈值

物体测量与特征抽取

1.测量周长、面积

在物体从图象中分割出来后，进一步就可以对它的几何特征进行测量和分析，在此基础上可以识别物体，也可以对物体分类，或对物体是否符合标准进行判别，实现质量监控。与图象分割一道，物体测量与形状分析在工业生产中有重要的应用，它们是机器视觉的主要内容之一。例如，能将马铃薯或苹果等农产品按品质自动分类的机器视觉系统，自动计算不规则形状所包含面积的测量系统，将传送带上不同工件自动分类的视觉系统，等等。

• 周长
  
  其中，$n_{\theta }$ 是链中具有奇数值的链码的个数，$n_0$是链中具有偶数值的链码的个数。
• 面积
  A=x2y1-1/2x1y2-1/2x2y2-1/2(x2-x1)(y2-y1)=1/2(x1y2-x2y1)

2.外接矩形

当物体从图象中分割出来以后，形状描述特征与尺寸测量结合起来可以作为区分不同物体的依据，在机器视觉系统中起着十分重要的作用。

①长度和宽度
在已知物体的边界时，用其外接矩形的尺寸来刻画它的基本形状是最简单的方法。如果仅计算其在坐标系方向上的外接矩形是很简单的，只需计算物体边界点的最大和最小坐标值，就可得到物体的水平和垂直跨度。但通常需要计算反映物体形状特征的主轴方向上的长度和与之垂直方向上的宽度，这样的外接矩形是物体最小的外接矩形（MER-Minimum Enclosing Rectangle）。
计算MER的一种方法是将物体在90度范围内等间隔地旋转，每次记录其坐标系方向上的外接矩形参数，取其面积为最小的矩形的参数为主轴意义下的长度和宽度。通常主轴可以通过矩（moments）的计算得到，也可以用求物体的最佳拟合直线的方法求出。

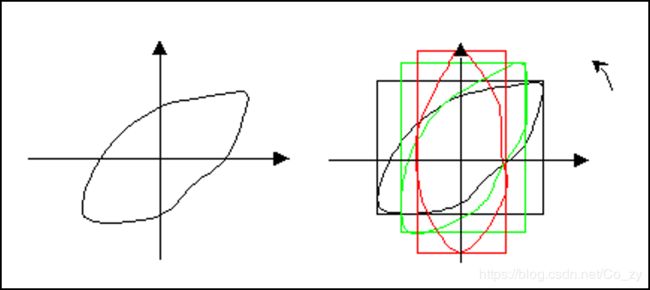
② 矩形度
矩形度用物体的面积与其最小外界矩形的面积之比来刻画，反映物体对其外接矩形的充满程度：
此外，另一个与形状有关的特征是长宽比 它可以将细长的物体与方形或圆形的物体区别开来。
③ 圆形度
圆形度用来刻画物体边界的复杂程度，它们在圆形边界时取最小值。最常用的圆形度是周长的平方与面积的比
④ 不变矩
矩的定义：对于二元有界函数f(x,y),它的(j+k)阶矩是：

特征提取

如何寻找右图中玩具车的位置

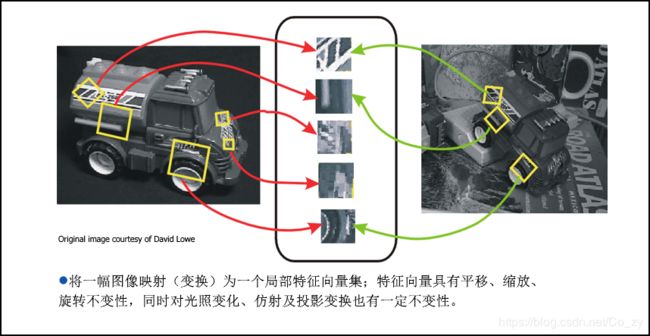
这就需要用到 <尺度不变特征变换匹配算法 Scale Invariant Feature Transform>
90年代British Columbia大学大卫.劳伊（David G.Lowe）教授总结了现有的基于不变量技术的特征检测方法，并正式提出了一种基于尺度空间的、对图像缩放、旋转甚至仿射变换保持不变性的图像局部特征描述算子－SIFT（尺度不变特征变换），这种算法在2004年被加以完善。

SIFT算法可以解决的问题

目标的自身状态、场景所处的环境和成像器材的成像特性等因素影响图像配准/目标识别跟踪的性能。而SIFT算法在一定程度上可解决：

• 目标的旋转、缩放、平移（RST）
• 图像仿射/投影变换（视点viewpoint）
• 光照影响（illumination）
• 目标遮挡（occlusion）
• 杂物场景（clutter）
• 噪声

SIFT算法的实质可以归为在不同尺度空间上查找特征点（关键点）的问题。

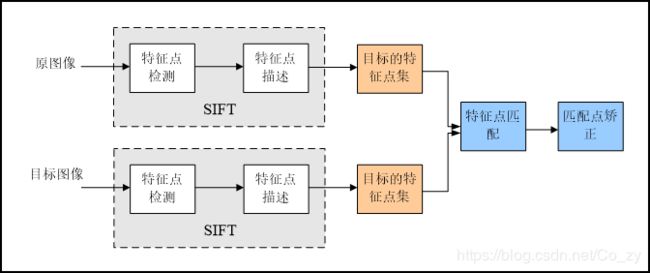
SIFT算法实现物体识别主要有三大工序，1、提取关键点；2、对关键点附加详细的信息（局部特征）也就是所谓的描述器；3、通过两方特征点（附带上特征向量的关键点）的两两比较找出相互匹配的若干对特征点

另参考 https://www.bilibili.com/video/av42629442

---

图像的频域变换

傅里叶变换, 看中国大学MOOC
https://www.icourse163.org/learn/WHUT-1003535158

数学形态学

暂时留坑

---

《第二部分》计算机视觉

2019-10-14 开始上计算机视觉
孙涵老师主页 http://www.sunnyimgtech.com/

计算机视觉课程内容

计算机视觉发展史，MarT视觉理论
人眼成像原理
纹理、颜色和光源
摄像机参数与模型，摄像机标定
双目视觉与立体观测
运动目标检测与跟踪
计算机视觉典型应用

10-25 梁栋老师代课内容

1.华为P30拍月亮是如何实现的
2.手机单镜头人脸识别是如何实现的?为何照片无法欺骗镜头
扩展:单镜头、多镜头的功能
3.合成孔径
4.景深

了解景深 这一篇就够了
https://zhuanlan.zhihu.com/p/55740729

光圈越大，景深越浅
光圈越小，景深越大

考试内容

《第三部分》医学图像

图像来源

X光
CT
Pet-CT
核磁共振 MRI
超声波(B超)

考试内容