用回溯递归算法解决走迷宫问题

迷宫是由许多小方格构成的矩形，在每个小方格中有的是墙，有的是路，走迷宫就是从一个小方格沿上下左右四个方向到临近的方格，当然不能穿墙。设迷宫的入口是在左上角（1,1），出口是右下角（8,8）根据给定的迷宫，找出一条从入口到出口的路径。

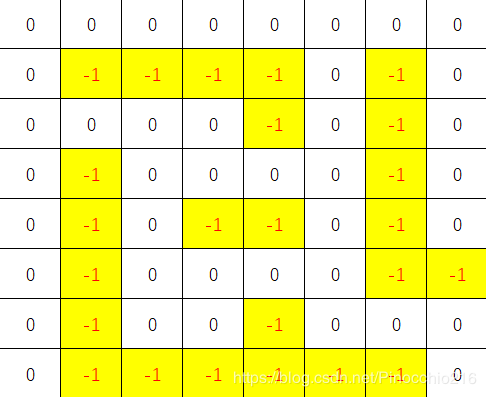
算法设计思路：从入口开始广度优先搜索所有可到达的方格入队，再扩展队首方格，直到搜索到出口时算法结束。
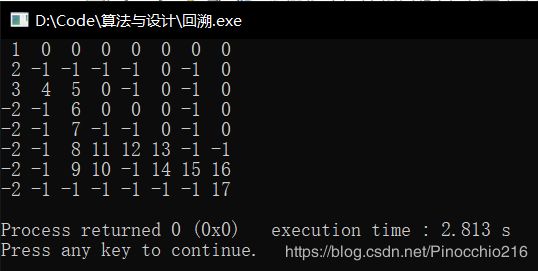
以0表示路，-1表示墙，-2标记死胡同，dep标记走过的步数。
下面直接上代码，可能会更好理解。

#include
int maze[8][8]=
{
    {0,0,0,0,0,0,0,0},
    {0,-1,-1,-1,-1,0,-1,0},
    {0,0,0,0,-1,0,-1,0},
    {0,-1,0,0,0,0,-1,0},
    {0,-1,0,-1,-1,0,-1,0},
    {0,-1,0,0,0,0,-1,-1},
    {0,-1,0,0,-1,0,0,0},
    {0,-1,-1,-1,-1,-1,-1,0}
},//以二维数组maze[8][8]存储整个迷宫
fx[4]= {1,-1,0,0},
       fy[4]= {0,0,-1,1};//fx和fy一起就可以实现在数组里进行上下左右四种变化
int i,j,k;
int dep;
void out()
{
    int i,j;
    for(i=0; i<8; i++)
    {
        for(j=0; j<8; j++)
            printf("%2d ",maze[i][j]);
        printf("\n");
    }
}//用于输出结果的函数
int check(int i,int j,int k)
{
    int flag=1;
    i=i+fx[k];
    j=j+fy[k];
    if(i<0||i>7||j<0||j>7)//是否在迷宫内部
        flag=0;
    else if(maze[i][j]!=0)//是否是可走的路线
        flag=0;
    return flag;
}//check函数用于检查该方格是否是可行的路线，可行就返回1否则返回0

void search(int i,int j)
{
    int k,newi,newj;
    for(k=0; k<4; k++)//从k=0到k=3这4次变化就实现了一个方格的上下左右移动
        if(check(i,j,k)==1)
        {
            newi=i+fx[k];
            newj=j+fy[k];
            maze[newi][newj]=++dep;//dep用于存储目前走过的步数，每有效移动一次就要自增
            if(newi==7&&newj==7)//在数组中，终点即为maze[7][7]
                out();
            else
                search(newi,newj);//如果不是终点，就继续向四周探索

        }
    maze[i][j]=-2;//如果发现四周没路了，就是走到死胡同了，此时就把死胡同的路线标记为-2
    dep--;//在标记死胡同的同时search找的其实是后退的路，所以步数dep要自减
}

int main()
{
    dep=1;
    maze[0][0]=dep;
    search(0,0);
    return 0;
}

注意虽然图上是从(1,1)到(8,8)，但是在数组里是从(0,0)到(7,7)的。
算法框架参考的是《算法设计与分析》课本上的内容，在此基础上有微调和改进。