2020牛客寒假算法基础集训营3 题解

A 牛牛的DRB迷宫I

非常简单的dp，每个位置dp[i][j]都由dp[i - 1][j] 和dp[i][j -1]转移而来。

#include 
using namespace std;
typedef long long ll;
const int maxn = 100 + 5;
const ll mod = 1e9 + 7;
 
int n, m;
char s[maxn][maxn];
ll dp[maxn][maxn];
 
int main()
{
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n; i++)
        scanf("%s", s[i] + 1);
        
    memset(dp, 0 ,sizeof(dp));
    dp[1][1] = 1;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++)
        {
            if(s[i][j - 1] == 'R' || s[i][j - 1] == 'B')
                dp[i][j] = (dp[i][j] + dp[i][j - 1]) % mod;
            if(s[i - 1][j] == 'D' || s[i - 1][j] == 'B')
                dp[i][j] = (dp[i][j] + dp[i - 1][j]) % mod;
        }
    }
    printf("%lld\n", dp[n][m]);
    return 0;
}

B 牛牛的DRB迷宫II

主对角线是B，B的下一斜列是R，上一斜列为D

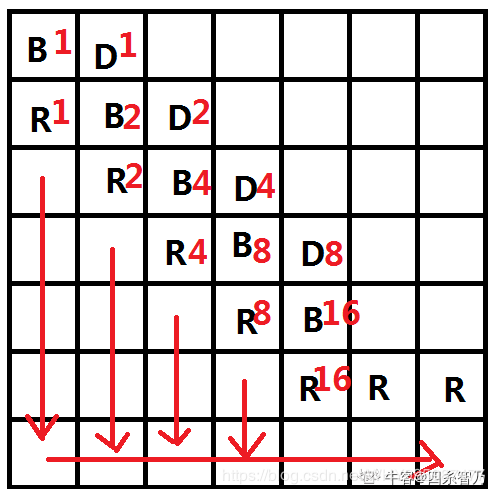
这样主对角线的值依次为1、2、4、8、16、……

二次幂的数字，也就是各个位为1的二进制数，可以通过配凑得到k。

图最大50*50，也就是说数字的范围在2⁵⁰ 以内，而题目给出的k要取模1e9+7的，所以是足够配出所有答案的。

先进行二进制位的分解，然后再对于二进制位1的那一列，从上往下写一列down下来，然后最下面一行都是right，这样就把答案叠加到右下角。

注意dp[n - 1][m - 1]和dp[n - 1][m]要改成R

#include
using namespace std;
typedef long long ll;
const ll mod = 1e9 + 7;
ll fac[100];
char G[100][100];
ll k;
int n = 35, m = 35;

int div(ll k)
{
    int pos = 0;
    while(k){
        fac[++pos] = k % 2;
        k /= 2;
    }
    return pos;
}

int main()
{
    scanf("%lld", &k);
    int len = div(k % mod);
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
        {
            if(i == j)
                G[i][j] = 'B';
            else
                G[i][j] = 'R';
        }

    for(int i = 1; i < n; i++)
        G[i][i + 1] = 'D';

    for(int i = 1; i <= len; i++)
    {
        if(fac[i])
        {
            G[i + 1][i] = 'B';
            for(int j = i + 2; j < n; j++)
                G[j][i] = 'D';
        }
    }
    G[34][34] = 'R';
    G[34][35] = 'R';
    printf("35 35\n");
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
            printf("%c",G[i][j]);
        printf("\n");
    }
    return 0;
}

C 牛牛的数组越位

按照题意模拟即可

#include 
using namespace std;
typedef long long ll;
const int maxn = 1e3 + 5;
const ll mod = 1e9 + 7;
int a[maxn][maxn];
int language = 1; //"Accepted"
void out_put(int n, int m){
    for(int i =  0; i < n; i++)
    {
        for(int j = 0; j < m; j++)
            printf("%d ", a[i][j]);
        printf("\n");
    }
}
 
int main(){
    int T;
    scanf("%d", &T);
    while(T--)
    {
        language = 1;
        memset(a, 0, sizeof(a));
 
        int n, m, p;
        scanf("%d %d %d", &n, &m, &p);
        for(int i = 1; i <= p; i++)
        {
            int x, y, val;
            scanf("%d %d %d", &x, &y, &val);
 
            int pos = m * x + y;//>= 0 小于等于n*m这没有非法访问
             
            int new_x = pos / m;
            int new_y = pos % m;
             
            if(pos < 0 || pos >= n * m)//优先判断runtime error
                language = 3; //"Runtime error"
            else if(language != 3 && (x < 0 || y < 0 || y >= m))//判断是否数组越界过
            {
                language = 2; //"Undefined Behaviour"
                a[new_x][new_y] = val;
            }
            else
                a[new_x][new_y] = val;
        }
         
        if(language == 1)
        {
            out_put(n, m);
            printf("Accepted\n");
        }
        else if(language == 2)
        {
            out_put(n, m);
            printf("Undefined Behaviour\n");
        }
        else
            printf("Runtime error\n");
    }
    return 0;
}

D 牛牛与二叉树的数组存储

按照题意模拟即可，用到了二叉树的性质。

原数组记得开二倍空间，初始化都为-1，不然查叶子结点的时候会WA

用pos数组存储位置信息，pos[i]表示数字 i 在 a[ ] 中的下标

#include 
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 5;
const ll mod = 1e9 + 7;
 
int a[maxn];
int pos[maxn];//数字i在a[]中的下标
 
int main()
{
    int n;
    scanf("%d", &n);
    memset(a, -1, sizeof(a));
 
    int tree_size = 0;
    int tree_root = 0;
 
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
 
        pos[a[i]] = i;
 
        if(a[i] > 0)
        {
            tree_size++;
            if(tree_size == 1)
                tree_root = a[i];
        }
    }
 
    printf("The size of the tree is %d\n", tree_size);
    printf("Node %d is the root node of the tree\n", tree_root);
 
    for(int i = 1; i <= tree_size; i++)
    {
        printf("The father of node %d is %d, the left child is %d, and the right child is %d\n", i, a[pos[i] / 2], a[ pos[i] * 2 ], a[ pos[i] * 2 + 1]);
    }
    return 0;
}

E 牛牛的随机数

数位dp

出题人的题解，写的很详细了

#include
using namespace std;
const long long mod=(int)1e9+7;
int i,i0,T;
long long cnta[70],cntb[70],dp[70][70][2],a[70];
long long dfs(int len,bool maxi,int k,bool f)
{
    if(dp[len][k][f]!=-1&&maxi==0)
        return dp[len][k][f];
    long long cnt=0;
    if(!len)
        return f;
    int maxn=maxi?a[len]:1;
    for(int i=0;i<=maxn;i++)
        cnt+=dfs(len-1,maxi&&i==a[len],k,f||len==k&&i);
    return maxi?cnt:dp[len][k][f]=cnt;
}
long long div(long long tmp,int k)
{
    memset(a,0,sizeof(a));
    int p=0;
    while(tmp)
        a[++p]=tmp%2,tmp/=2;
    return dfs(p,1,k,0);
}
long long inv(long long x,long long mod)
{
    long long k=mod-2,ans=1;
    while(k){
        if (k&1) ans=ans*x%mod;
        x=x*x%mod;
        k>>=1;
    }
    return ans;
}
int main()
{
    memset(dp,-1,sizeof(dp));
    scanf("%d",&T);
    while(T--)
    {
        long long l1,r1,l2,r2,p=1,ans=0;
        scanf("%lld %lld %lld %lld",&l1,&r1,&l2,&r2);
        l1--,l2--;
        for(i=1;i<=60;i++,p*=2)
        {
            cnta[i]=div(r1,i)-div(l1,i);
            cntb[i]=div(r2,i)-div(l2,i);
            ans+=(cnta[i]%mod*((r2-l2-cntb[i])%mod)%mod+cntb[i]%mod*((r1-l1-cnta[i])%mod)%mod)*(p%mod)%mod;
            ans%=mod;
            
        }
        ans%=mod,ans+=mod,ans%=mod;
        ans=ans*inv(((r1-l1)%mod)*((r2-l2)%mod)%mod,mod)%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

F 牛牛的Link Power I

水题，手推一下，可以发现，存储一下1的位置就能快速求解答案。

#include 
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
const ll mod = 1e9 + 7;
char s[maxn];
int pos[maxn];
int main()
{
    ll n;
    scanf("%lld", &n);
    scanf("%s", s + 1);
    ll ans = 0, cnt = 0;
    for(int i = 1; i <= n; i++)
        if(s[i] == '1')
            pos[cnt++] = i;        
    ll num = cnt - 1;
    for(ll i = 0; i < cnt - 1; i++)
    {
        ans = ( ans - num * pos[i] ) % mod;
        ans = ( ans + (i + 1) * pos[i + 1] ) % mod;
        num--;
    }
    printf("%lld\n", ans);
    return 0;
}
/*
12
001001010001
*/

G 牛牛的Link Power II

用线段树即可，维护距离。代码实现很简单，但是出题人挺厉害的，代码实现的思路很巧妙。

做法是维护一个ans值，一开始线段树pre只往后更新，这样往前查就不会多算。

另一个sur只往前更新，这样往后查就不会多算。

对于每个修改，修改位置为x，pre的[1, x - 1]和sur的[x + 1, n]之和就是变化量，正负看是变成 1 还是变成 0 ，然后用这个变化量更新ans，同时对线段树区间修改即可。

#include
using namespace std;
const int MAXN=100005;
const long long mod=1e9+7;
char s[MAXN];
int n,m,x,q;
long long ans;
struct tnode
{
    long long sum,lazy;
    int l,r;
};
struct Segment_Tree
{
    tnode t[4*MAXN];
    void pushdown(int root)
    {
        if(t[root].lazy!=0)
        {
            t[root].sum+=t[root].lazy*(t[root].r-t[root].l+1);
            if(t[root].l!=t[root].r)
            {
                int ch=root<<1;
                t[ch].lazy+=t[root].lazy;
                t[ch+1].lazy+=t[root].lazy;
            }
            t[root].lazy=0;
        }
    }
    void update (int root)
    {
        int ch=root<<1;
        pushdown(ch);
        pushdown(ch+1);
        t[root].sum=t[ch].sum+t[ch+1].sum;
    }
    void build(int l,int r,int root=1)
    {
        t[root].l=l;
        t[root].r=r;
        if(l!=r)
        {
            int mid=(l+r)>>1;
            int ch=root<<1;
            build(l,mid,ch);
            build(mid+1,r,ch+1);
            update(root);
        }
        else t[root].sum=0;
    }
    void change(int l,int r,long long delta,int root=1)
    {
        if(l==t[root].l&&r==t[root].r)
        {
            t[root].lazy+=delta;
            pushdown(root);
            return;
        }
        int mid=(t[root].l+t[root].r)>>1;
        int ch=root<<1;
        if(r<=mid)change(l,r,delta,ch);
        else if(l>mid)change(l,r,delta,ch+1);
        else {change(l,mid,delta,ch);change(mid+1,r,delta,ch+1);}
        update(root);
    }
    long long sum(int l,int r,int root=1)
    {
        pushdown(root);
        if(t[root].l==l&&t[root].r==r)
        {
            return t[root].sum;
        }
        int mid=(t[root].l+t[root].r)>>1;
        int ch=root<<1;
        if(r<=mid)return sum(l,r,ch);
        else if(l>mid)return sum(l,r,ch+1);
        else return sum(l,mid,ch)+sum(mid+1,r,ch+1);
    }
};
Segment_Tree pre,suf;
int main()
{
    scanf("%d",&n);
    scanf("%s",s+1);
    pre.build(1,n);
    suf.build(1,n);
    for(int i=1;i<=n;++i)
    {
        if(s[i]=='1')
        {
            ans=(ans+pre.sum(1,i))%mod;
            if(i!=n)pre.change(i+1,n,1);
            if(i!=1)suf.change(1,i-1,1);
        }
    }
    printf("%lld\n",ans);
    scanf("%d",&m);
    for(int i=1;i<=m;++i)
    {
        scanf("%d %d",&q,&x);
        long long pres=pre.sum(1,x);
        long long sufs=suf.sum(x,n);
        if(q==1)
        {
            ans=(ans+pres+sufs)%mod;
            if(x!=n)pre.change(x+1,n,1);
            if(x!=1)suf.change(1,x-1,1);
        }
        else
        {
            ans=((ans-pres-sufs)%mod+mod)%mod;
            if(x!=n)pre.change(x+1,n,-1);
            if(x!=1)suf.change(1,x-1,-1);
        }
        printf("%lld\n",ans);
    }
    return 0;
}

H 牛牛的k合因子数

水题，用素数筛筛一下，然后统计各个k合因子数的个数，直接输出就好了。

#include 
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
const ll mod = 1e9 + 7;
int is_prime[maxn], ans[maxn], n, m;
void init(int n)
{
    for(int i = 1; i <= n; i++)
        is_prime[i] = 1;
 
    is_prime[1] = 1;
 
    for(int i = 2; i <= n; i++)
    {
        if(!is_prime[i])
            continue;
        for(int j = i + i; j <= n; j += i)
            is_prime[j] = 0;
    }
}
 
void init2(int n)
{
    for(int i = 1; i <= n; i++)
    {
        int cnt = 0;
        for(int j = 1; j * j <= i; j++)
        {
            if(i % j == 0)
            {
                int num = i / j;
                if(num == j)
                {
                    if(!is_prime[num])
                        cnt++;
                }
                else
                {
                    if(!is_prime[num])
                        cnt++;
                    if(!is_prime[j])
                        cnt++;
                }
            }
        }
        ans[cnt]++;
    }
}
 
int main()
{
    scanf("%d %d", &n, &m);
    init(n);
    init2(n);
 
    for(int i = 1; i <= m; i++)
    {
        int num;
        scanf("%d", &num);
        printf("%d\n", ans[num]);
    }
    return 0;
}

I 牛牛的汉诺塔

不了解汉诺塔可以看看这个视频
https://www.bilibili.com/video/av82006662?from=search&seid=14526053186161103983
直接将题目给出的python代码改成c++，然后再改成记忆化搜索即可，也可以用递推。

这份代码是题解人给出的。
https://ac.nowcoder.com/discuss/365306?type=101&order=0&pos=5&page=1

#include
using namespace std;
struct node
{
    long long data[6];
    node()
    {
        memset(data,0,sizeof(data));
    }
    //A->B      0
    //A->C      1
    //B->A      2
    //B->C      3
    //C->A      4
    //C->B      5
};
node operator + (const node &A,const node &B)
{
    node C;
    for(int i=0;i<6;++i)
    {
        C.data[i]=A.data[i]+B.data[i];
    }
    return C;
}
void moveto(int x,int y,node &temp)
{
    if(x==0&&y==1)++temp.data[0];
    if(x==0&&y==2)++temp.data[1];
    if(x==1&&y==0)++temp.data[2];
    if(x==1&&y==2)++temp.data[3];
    if(x==2&&y==0)++temp.data[4];
    if(x==2&&y==1)++temp.data[5];
    return;
}
node dp[3][3][3][105];
bool vis[3][3][3][105];
node hanoi(int a,int b,int c,int n)
{
    if (vis[a][b][c][n])return dp[a][b][c][n];
    if (n==1)
    {
        moveto(a,c,dp[a][b][c][n]);
        vis[a][b][c][n]=true;
        return dp[a][b][c][n];
    }
    node temp;
    temp=temp+hanoi(a,c,b,n-1);
    moveto(a,c,temp);
    temp=temp+hanoi(b,a,c,n-1);
    vis[a][b][c][n]=true;
    return dp[a][b][c][n]=temp;
}
int n;
int main()
{
    scanf("%d",&n);
    node ans=hanoi(0,1,2,n);
    printf("A->B:%lld\n",ans.data[0]);
    printf("A->C:%lld\n",ans.data[1]);
    printf("B->A:%lld\n",ans.data[2]);
    printf("B->C:%lld\n",ans.data[3]);
    printf("C->A:%lld\n",ans.data[4]);
    printf("C->B:%lld\n",ans.data[5]);
    printf("SUM:%lld\n",(1LL<<n)-1);
}

J 牛牛的宝可梦Go

有k个宝可梦，我们大概知道，要先考虑那些先出现的，然后再考虑那些后出现的。

也就是说会有一个步骤是把宝可梦按出现时间进行排序。

然后如何考虑呢，用dp，图很小，只有200个结点，所以走两百步必定能从一个点走到图中的任意的另一个点上，那么我们每个dp[i]只要往前跑200步即可，对于200步之前的，我们用一个pre_max来维护它们的最大值，这样就能在O（200*k）的时间复杂度完成。

当然要先跑一遍floyd跑出最短距离，dp时需要判断是否能抓到。

#include
using namespace std;
typedef long long ll;
const ll mod = 1e9 + 7;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int maxn_p = 2e2 + 5;
const int maxn_k = 1e5 + 5;

int n, m, k;
ll dis[maxn_p][maxn_p];
ll dp[maxn_k];
ll pre_max, ans;

struct node{
    int p, t;
    ll val;
}a[maxn_k];

bool cmp(node a, node b){
    return a.t < b.t;
}

int main()
{
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            dis[i][j] = (i == j) ? 0 : INF;
        }
    }

    int u, v;
    for(int i = 1; i <= m; i++)
    {
        scanf("%d %d", &u, &v);
        dis[u][v] = dis[v][u] = 1;
    }

    for(int k = 1; k <= n; k++)
    {
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= n; j++)
            {
                dis[i][j] = min(dis[i][k] + dis[k][j], dis[i][j]);
            }
        }
    }

    scanf("%d", &k);
    for(int i = 1; i <= k; i++){
        scanf("%d %d %lld", &a[i].t, &a[i].p, &a[i].val);
    }

    sort(a + 1, a + 1 + k, cmp);
    a[0].p = 1;
    for(int i = 1; i <= k; i++)
    {
        if(i > 200)
        {
            pre_max = max(pre_max, dp[i - 200]);
            dp[i] = a[i].val + pre_max;
        }
        else
        {
            dp[i] = -INF;
        }

        for(int j = 1; j <= 200 && i - j >= 0; ++j)
        {
            if(a[i].t - a[i - j].t >= dis[a[i].p][a[i-j].p])
            {
                dp[i] = max(dp[i], dp[i - j] + a[i].val);
            }
        }
        ans = max(ans, dp[i]);
    }
    printf("%lld\n", ans);
    return 0;
}