数据结构系列文章:
- 常用的排序
- 二叉树的4种遍历
- 八皇后问题
八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。 高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解,后来有人用图论的方法解出92种结果。计算机发明后,有多种计算机语言可以解决此问题。
回溯法[试探法,递归]和迭代法
基本思路是:
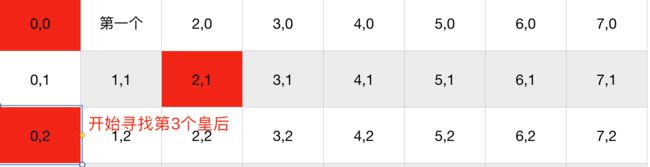
1.第一行先占一个皇后
2.第二行再占一个且不能与第一个皇后攻击
3.第三行再占一个
。。。。。
n.第n行占一个,当第n行站不下的时候,取消n-1行的皇后,在第n-1皇后的下一个位置重新占一个皇后位置,知道占到最n-1行的最后一个位置,当还不行的时候,就取消第n-2行,当n-2行的皇后在n-2行的最后一个位置的时候,就取消n-3,n-2在最后一个位置,那么n-3行的一定不再最后一个位置。
再重新寻找n-2行的皇后的位置。
。。。。
。。。。
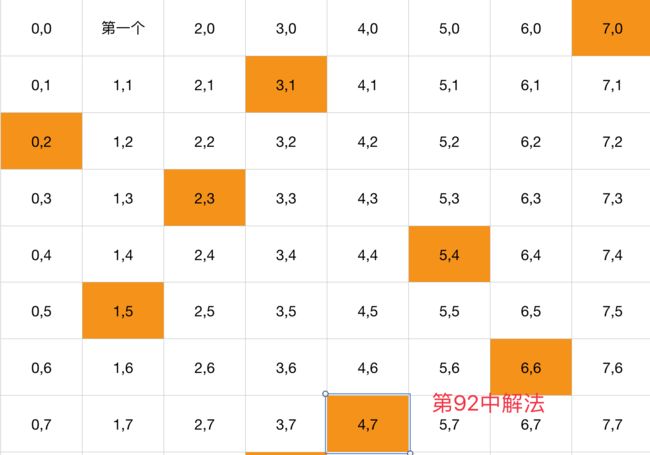
直到找到最后一个皇后。
找完第一种解法,重新开始寻找第二种解法,直接第一个皇后占第一行的第2个位置,寻找第三种解法占第一行的第3个位置。。。。直到寻找第n个解法。code 在下边。代码是Swift,正好可以练习练习语法。
详细步骤:
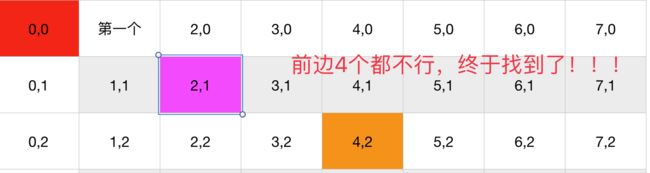
1.判断新的皇后是否与已经存在的皇后打架,加入是第一个则不用判断直接加入。
2.第二行新生成的皇后,然后与第一行判断是否打架,是的话,向右移动一个格子,否则添加上去。
3.第三行从左至右从第一个格子开始,判断是否与上面所有的皇后打架,是的话,向右移动一个格子,否则添加上去。
。。。
。。。
8.到第八行,新生成一个皇后,判断是否与上面所有的皇后打架,没有则添加。有则向右移动一个格子。当移动至一个不打架的格子,则一个解法已经生成。向后则寻找第二个方案,将第8行的皇后删除,新生成的皇后在刚才最后一个皇后的右边,为什么在右边呢?因为左边刚才已经判断过都失败了,所以新生成的在右边,然后在判断是否与上边的皇后打架。
9.当向右移动最后一个格子而且与上边的皇后打架,则删除掉此皇后,然后把上一行的皇后向右移动一个格子,第8行从左向右从0开始生成一个新的皇后。然后 步骤8.
10.直到第一行的皇后走到第一行的最后一个,第二行也找到最后一个格子的皇后,而且失败,则是所有解法都寻找完成。
在开始寻找第93种解法的时候,是这样子
只好删除了第一行的,第一行的向右移动,发现第一行其实已经是最后一个了,解法全部寻找完成
struct QueenHandle {
//一次的解法皇后
var queensArray:[Queen] = [Queen]();
//所有解法
var queensWay:[[Queen]] = [[Queen]]();
init() {
}
func canStandWithOthers(queens:[Queen],queen:Queen) -> Bool {
var pass = true;
let count = queens.count;
if count == 0 {
return true;
}
for k in 0.. Void {
let q = Queen(locations: Point(x: x, y: y));
//位置是否可用
let can = self.canStandWithOthers(queens: self.queensArray, queen: q);
if can {
//添加皇后
self.queensArray.append(q);
y += 1;
x = 0;
if y > yMax
{
if (self.queensArray.count == n){
//解法完毕 继续下一个解法
self.queensWay.append(self.queensArray);
self.queensArray.removeAll();
x = self.queensWay.count;
y = 0;
if (x == n){return}else{
callback(x: &x, y: &y, n: &n, xMax: xMax, yMax: yMax);
}
}else{
//回溯法核心思路 当n行没有合适位子,删除上一行的皇后,重新寻找上一行的新皇后位子
if self.queensArray.count > 0{
let lastQ = self.queensArray.removeLast();
x = lastQ.locations.x + 1;
y -= 1;
}
}
}else if(y <= yMax){
callback(x: &x, y: &y, n: &n, xMax: xMax, yMax: yMax);
}
}else if(x < xMax){
x += 1;
callback(x: &x, y: &y, n: &n, xMax: xMax, yMax: yMax);
}else if(x >= xMax){
if self.queensArray.count > 0{
let lastQ = self.queensArray.removeLast();
x = lastQ.locations.x + 1;
y -= 1;
if x > xMax{
let lastQ = self.queensArray.removeLast();
x = lastQ.locations.x + 1;
y -= 1;
}
callback(x: &x, y: &y, n: &n, xMax: xMax, yMax: yMax);
}
}
}
public mutating func handle() -> Void {
var number = 0
while number<8 {
self.find(index: number);
//首行的8种可能
if self.queensArray.count == 8 {
self.queensWay.append(self.queensArray);
}
self.queensArray.removeAll();
number += 1;
}
}
public mutating func find(index:Int) -> Void
{
var y = 0;
var x = index;
while y<8 {
while x<8{
let queen = Queen(locations: Point(x: x, y: y));
let count = self.queensArray.count;
if count>0 {
var pass = true;
for k in 0.. 0{
while x > 7{
//回溯法 寻找上一个可能的皇后 当x==8,继续找上一行的皇后
x = self.queensArray.removeLast().locations.x + 1;
y -= 1;
}
}else{
y += 1;
}
}
}
}
public func printWays() -> Void{
let count = self.queensWay.count;
for i in 0.. 0c版本递归
//
-(void)callBackx:(NSInteger )x
y:(NSInteger)y
number:(NSInteger)number
maxXY:(NSInteger)max{
Queen *q = [[Queen alloc] initWithX:x X:y];
if ([FYQueenHandle fightQueen:q
inList:self.queensLine] == NO) {
[self.queensLine addObject:q];
if (self.queensLine.count == number) {
[self.queenMutArray addObject:self.queensLine];
[self.queensLine removeLastObject];//删除最后的那一个皇后
x += 1;
if (x > max) {
if (self.queensLine.count) {
Queen *last =self.queensLine.lastObject;
[self.queensLine removeLastObject];
x = last.x + 1;
y = last.y;
}
}
[self callBackx:x y:y
number:number
maxXY:max];
}else{
x = 0;
y ++;
[self callBackx:x y:y
number:number
maxXY:max];
}
}else{
x += 1;
if (x > max) {
if (self.queensLine.count) {
Queen *last =self.queensLine.lastObject;
[self.queensLine removeLastObject];
x = last.x + 1;
y = last.y;
}
if (x > max) {//超出最大值
if (self.queensLine.count) {
Queen *last2 =self.queensLine.lastObject;
[self.queensLine removeLastObject];
x = last2.x + 1;
y = last2.y;
}else{
return;//第一行最后一个的情况 直接返回
}
}
[self callBackx:x y:y
number:number
maxXY:max];
}else{
[self callBackx:x y:y
number:number
maxXY:max];
}
}
}
0c版本迭代
+(BOOL)fightQueen:(Queen *)queen inList:(NSArray *)array
{
BOOL pass = NO;
if (array.count == 0) {
return NO;
}
for (Queen * item in array) {
NSInteger xx = labs(item.x - queen.x);
NSInteger yy = labs(item.y - queen.y);
BOOL is = xx == yy ? YES:NO;
if (item.x == queen.x ||
item.y == queen.y || is
) {
pass = YES;
break;
}
}
return pass;
}
- (void)handle{
for (NSInteger y = 0; y < 8; y ++) {
for (NSInteger x = 0; x < 8; x ++) {
Queen *q = [Queen new];
q.x = x;
q.y = y;
if( [FYQueenHandle fightQueen:q
inList:self.queensLine] == NO){
[self.queensLine addObject:q];
if (self.queensLine.count == 8) {
[self.queenMutArray addObject:[self.queensLine copy]];
[self.queensLine removeLastObject];
if (x == 7) {
if (self.queensLine.count) {
Queen * last = self.queensLine.lastObject;
x = last.x;
y = last.y;
[self.queensLine removeLastObject];
}else{
x = 8;//跳出循环
y = 8;
}
}
}else{
break;//跳出来y +1
}
}else{//添加不上去
if (x == 7) {
if (self.queensLine.count) {
Queen * last = self.queensLine.lastObject;
x = last.x;
y = last.y;
[self.queensLine removeLastObject];
if (x == 7) {
if (self.queensLine.count) {
Queen * last2 = self.queensLine.lastObject;
x = last2.x;
y = last2.y;
[self.queensLine removeLastObject];
}else{
y = 8;
x = 8;
}
}
}else{
x = 8;//跳出循环
y = 8;
}
}
}
}
}
}
点我下载代码