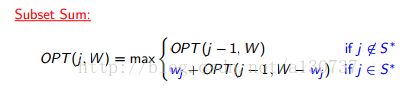subset problem(子集和问题)
给定一个包含N个非负数的set, 并且给定K, 从集合中找出一组元素子集, 使得这组子集的各个元素相加起来和是K。
注意, 我们假设输入的set 中的各个元素均是unique的(即 no duplicates present)。
方法一(穷竭搜索subset sum).。 一个比较naive的办法就是考虑这个集合的所有可能的subsets。 不难看出, 给定集合(N个元素)的subset的个数是:
2^(N)。
方法二(backtracking)也就是采取回溯算法。 在穷竭搜索中, 我们只是对所有的子集进行测试, 不管他们值不值得我们去测试。 回溯法通过对选择的元素做一个systematic consideration, 从而减少了需要测试的子集的数目, 这是一个改进。
下面, 举一个例子。 一个set有四个elements w[1], w[2], w[3], w[4]。 其中我们设计回溯算法的时候, 采用tree diagram, 表示要产生的所有可能的集合。
例如, W = {2, 4, 6, 8, 10}, 现在问题是从集合W中选择一个子集合, 是的子集内部的所有的元素相加为20。 不难看出, 权重相加为20的答案有三个: {2, 4, 6, 8}, {2, 8, 10}, {4, 6, 10}。
我们可以使用一个bit vector 表示得到的solution, 如果某个元素被选中了, 那么在bit vector 对应的索引下记为1, 否则, 没有选中记为0. 所以解为: {1, 1, 1, 1, 0}, {1, 0, 0, 1, 1}和 {0, 1, 1, 0, 1}。 我们接下来可以创建一个二叉树, 其中level i 代表权重wi。 每一个节点引出两个branch, 一个branch标记为0, 一个标记为1. 标记为0的意思是这个branch引出的孩子节点对应的weight不再答案选中, 标记为1表示引出的child选中。 所以向量(1, 0, 1)表示从节点开始, 选中left branch, 然后右边branch, 然后再左边的branch。 要找到所有可能的答案, 就得遍历这棵树, 然后只要和为M, 就打印出从根节点到这条路径所有的节点即可。
回溯算法使用的是深度遍历的方式遍历这棵树。 当已经知道当前的branch不可能得到solution, 就放弃这个branch, 回到父节点, 尝试下一个branch。 一直进行下去。
判断一个branch 是否应该被放弃, 需要测试条件。 我们假设我们在level k 的时候, 我们积累到的和为S, 由于我们的所有的权重都是事先排好序, 从小到大的, 所以如果 S + wk > M, 那么我们就知道, 再沿着这条branch下去, 不可能得到解的。 只要还有能够找到解的possible, 我们就沿着这个branch继续找。
算法伪代码如下:
程序如下:
#include
#include
#include
using namespace std;
void print(bitset<5> & X) {
for(int i = 0; i < X.size(); ++i) {
cout << X[i] << " ";
}
cout << endl;
}
void subsetSum(vector& W, bitset<5>& X, int sum, int targetSum, int k) {
X[k] = 1; // try one branch of tree
if(sum + W[k] == targetSum)
print(X); // we have a solution
else if(k + 1 <= W.size() && sum + W[k] <= targetSum)
subsetSum(W, X, sum + W[k], targetSum, k + 1);
if(k + 1 <= W.size() && sum + W[k + 1] <= targetSum) {
X[k] = 0; // try another branch
subsetSum(W, X, sum, targetSum, k + 1);
}
}
int main() {
vector W = {2, 4, 6, 8, 10};
bitset<5> X ;
subsetSum(W, X, 0, 20, 0);
return 0;
}
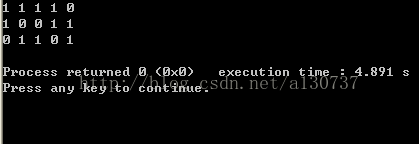
方法三(动态规划) 首先, 我们定义isSubsetSum(int set[], int sum)函数返回一个bool 表示在集合中是否找得到子集是的和为某个sum。
上述问题可以分成两个子问题:
a) 包含最后一个元素的子集合, 对 n = n - 1, sum = sum - set[n-1]进行递归,
b) 不包含最后一个元素, 对n = n -1 进行递归。
如果上述两个子问题由一个返回true, 则最终的结果返回true。 这样, 我们有如下的相关的观察:
isSubsetSum(set, n, sum) = isSubsetSum(set, n-1, sum) ||
isSubsetSum(arr, n-1, sum-set[n-1])
Base Cases:
isSubsetSum(set, n, sum) = false, if sum > 0 and n == 0
isSubsetSum(set, n, sum) = true, if sum == 0 naive 的递归实现如下:
#include
// returns true if there is a subset set[]
// with sum equals to given sum
bool isSubsetSum(int set[], int n, int sum) {
// base case
if(sum == 0)
return true;
if(n == 0 && sum != 0)
return false;
// if last element is greater than sum,
// ignore it
if(set[n - 1] > sum)
return isSubsetSum(set, n -1, sum);
// else check if sum can be obtained by
// by the following
// a) including the last element
// b) excluding the last element
return isSubsetSum(set, n - 1, sum) || isSubsetSum(set, n - 1, sum - set[n - 1]);
}
// driver program
int main() {
int set[] = {3, 34, 4, 12, 5, 2};
int sum = 9;
int n = sizeof(set) / sizeof(set[0]);
if(isSubsetSum(set, n, sum) == true) {
printf("okay");
}
else {
printf("No");
}
return 0;
}
上述算法的最坏的时间复杂度是exponential。
其实子集和问题是一个NP的问题(没有已知的polynomial time的算法)。
但是我们可以使用动态规划的办法在pseudo polynomial的时间内解决这个问题。 我们的做法是:
创建一个2D的boolean table subset[i][j]。 然后自底向上的方式(所以没有递归)填充这个二维布尔数组。 如果存在一个子集合set[0..j-1],, 使得这个子集合的和等与i, 我们就记录subset[i][j]为true, 否则填充为false。 最后我们只需要返回subset[sum][n]即可。
程序如下:
// A Dynamic Programming solution for subset sum problem
#include
// Returns true if there is a subset of set[] with sun equal to given sum
bool isSubsetSum(int set[], int n, int sum) {
// The value of subset[i][j] will be true if there is a subset of set[0..j-1]
// with sum equal to i
bool subset[sum+1][n+1];
// If sum is 0, then answer is true
for (int i = 0; i <= n; i++)
subset[0][i] = true;
// If sum is not 0 and set is empty, then answer is false
for (int i = 1; i <= sum; i++)
subset[i][0] = false;
// Fill the subset table in botton up manner
for (int i = 1; i <= sum; i++)
{
for (int j = 1; j <= n; j++)
{
//
subset[i][j] = subset[i][j-1];
if (i >= set[j-1])
subset[i][j] = subset[i][j] || subset[i - set[j-1]][j-1];
}
}
return subset[sum][n];
}
// Driver program to test above function
int main()
{
int set[] = {3, 34, 4, 12, 5, 2};
int sum = 9;
int n = sizeof(set)/sizeof(set[0]);
if (isSubsetSum(set, n, sum) == true)
printf("Found a subset with given sum");
else
printf("No subset with given sum");
return 0;
}
运行结果如下: