JS 中 Math 对象的【三角函数】的用法与实战例子【打靶游戏】 | Math.tan(), Math.cos(), Math.sin()

不少人在学习JavaScript的时候，都知道有那么一个用于数学计算的类 Math，现在来简单回顾以下，强大的 Math 类中，有哪些属性和哪些方法：

如果用JS做前端的时候，就会发现跟 Math 类打交道比较少。但是如果用 Node.js  做后台，或用 JS 写游戏的时候，Math 类就会无处不在，尤其是 random()、round()、abs()、ceil()、floor() 等方法很常用。本篇文章就来说说Math 类中的 sin()、cos()、tan() 这三个中学时期的数学重点究竟在JS中怎么用。

一、理论部分

Math 类的 sin(x)、cos(x)、tan(x) 中的 x 参数是弧度，那么，弧度是什么？

最直观地说，一个 60度 的角，可以用 60°来表示，也可以用 π / 3 （圆周率除以3）来表示；

同理，一个 90度 的角，可以用 90°来表示，也可以用 π / 2 （圆周率除以2）来表示；

还有，一个 180度 的角，可以用 180°来表示，也可以用 π 来表示。

那么，【60°=π / 3】，【90°=π / 2】，【180°=π】，等号的左边是度数，右边是弧度。

是否回忆起来一个这么的例子，【 cos(60°) = cos(π/3 ) = 1/2 = 0.5 】

换句话说，一个角度，可以用度数来表示，也可以用弧度来表示。因为弧度更加符合计算机的计算模式，所以，Math 类的 sin(x)、cos(x)、tan(x) 中的 x 参数类型为弧度。

中学时期，我们知道，30、45、60、90、180 这些角度是特殊角，用弧度来表示相对容易，所以我们当时只背了这么特殊角度的弧度值，然后理所当然地，慢慢地遗忘了弧度的概念，本文也不阐述弧度的概念，而是直接上一条公式，怎么转换度数为弧度值：

------------------------------------------------------------

弧度 = 角度 × π / 180

-----------------------------------------------

怎么应用到代码里面？

var angle = 60;    //假设角度为60度

var radian = angle * Math.PI / 180;    //计算出弧度

console.log( Math.cos(radian) );    //输出cos 60度的值

用法就这么简单！理论部分到此结束，接下来讲一点实战部分。

二、实战部分

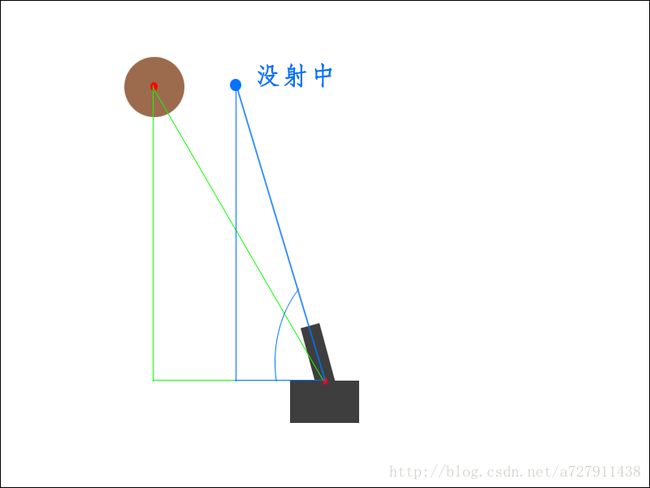
需求：做一个小游戏，有一把枪，一个靶子。枪头的角度可以旋转，靶子可以左右移动。现在要控制枪头对准移动的靶子射击，直到靶子射到烂为止。（下图为简单的图形界面，红点为锚点）

整一个小游戏的开发都很简单。只有在碰撞的实现上有点难度，传统做法，每次一开枪，射出去的子弹一碰到靶子就视为打中靶子。

现在问题是，传统做法中的子弹如果速度太快的情况下，碰撞检测很大可能会失效（原理请自己翻阅游戏开发相关书籍）。所以，不能用传统做法来实现碰撞，那怎么办？想象一下，子弹的射击速度非常快，一开枪，一瞬间，就会沿着瞄准的方向射去。我们只需要在开枪的时候，判断靶子是否与射线碰撞了，如果碰撞则射中，否则射偏。

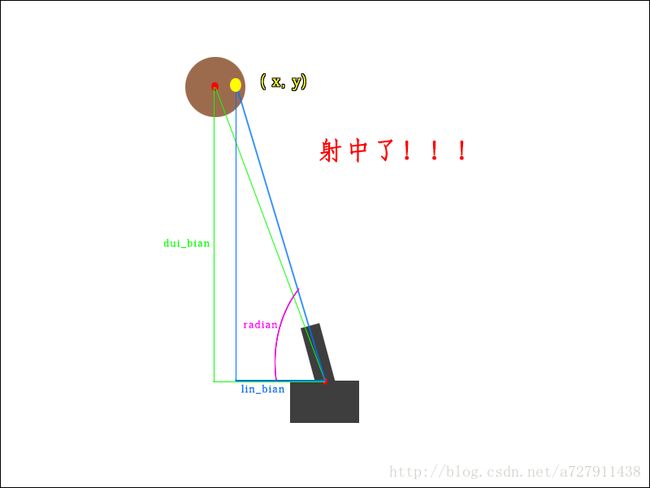
有了这个思路，就可以扩展了，加上枪头的旋转，和靶子的移动需求后，实现这个碰撞就需要用到三角函数了！为了便于理解，画一下原理图：

根据原理图，我们可以细化代码实现的每一步的原理：

1、先计算出枪头跟靶子的垂直方向距离（dui_bian）。

2、将枪头的旋转的角度转化为弧度（radian）。

3、根据弧度（radian）和枪头跟靶子的垂直方向距离（dui_bian）两个已知量可以计算出武器真正射击的子弹到目标位置的水平距离（lin_bian）。

4、通过枪头跟靶子的垂直方向距离（dui_bian）和武器真正射击的子弹到目标位置的水平距离（lin_bian）与偏移值计算，可以得出一个坐标（x, y）。

5、判断坐标（x, y）是否在靶子内部，是则视为打中靶子，否则就是打偏了。

有人要问，本文的内容不是关于三角函数的应用吗？请注意第3步，确实是用到了三角函数的 Math.tan() 方法。

写一个伪代码吧：

var lin_bian = dui_bian / Math.tan( radian );      //计算出武器真正射击的子弹到目标位置的水平距离（lin_bian）

正文结束！

本文有误之处，欢迎指点！