白色相簿2 coda篇各结局概率分析

本人很喜欢一款叫做白色相簿2的游戏，最近闲得无聊研究了一下coda中各结局的概率，在这里和各位喜欢二次元和算法的朋友交流

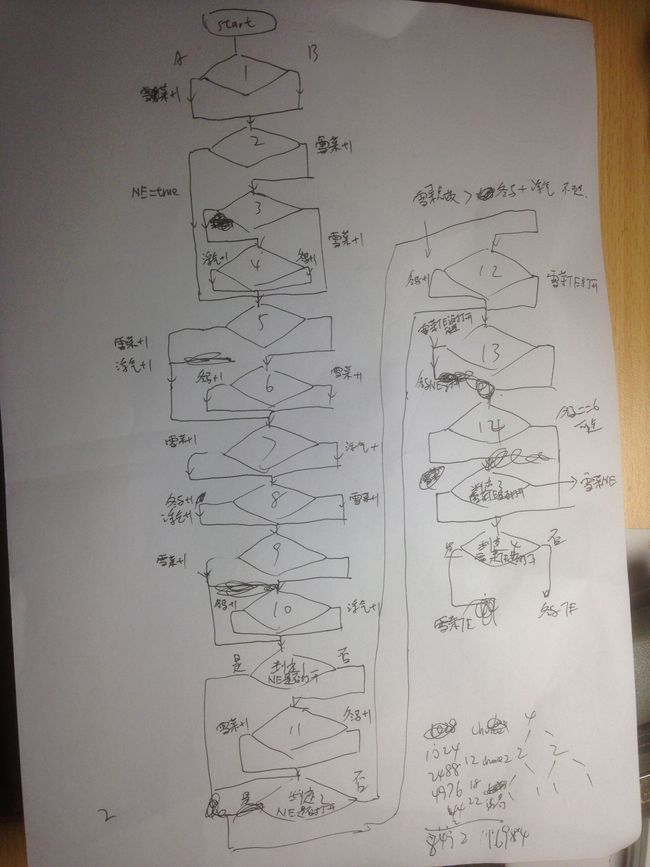
首先，coda篇中选项好感度变化大家可以看这一篇贴吧帖子https://tieba.baidu.com/p/3716041711。我把它画成了流程图（字比较潦草），这里上传上来给大家简单看一下。

可以看到整个过程非常错综复杂。如果只有选项或者判定那么计算概率还会容易一些，但这里还有一些选项会由于好感度不同而被屏蔽，鄙人深感自己数学功力不足，于是决定借助计算机来帮助解决问题。

接下来说说鄙人是怎么设计算法的：

我将每一个选项，判定或者结局用结构体Choice来表示。Choice主要起到两个作用，其一便是存储到当前Choice的各种数值，我这里定义了三个变量kazusa，setsuna，fq分别存储到当前Choice为止的冬马好感度，雪菜好感度以及浮气度，接着定义两个布尔类型neFlag，setsunaFlag分别表示NE的flag和雪菜TE的flag；其二便是要为下一个Choice做指引，这里就相对比较复杂。我这里定义了好多变量，首先定义了三个int变量deltaKazusa，deltaSetsuna，deltaFq分别来表示选项对于冬马好感度，雪菜好感度以及浮气度的变化关系，这三个变量可以分别取0,1,2，比如deltaKazusa取0表示没有选项会对冬马好感度起作用，deltaSetsuna取1表示选项A会对雪菜好感度起作用，取2表示选项B会对雪菜好感度起作用，接着定义两个int类型openNEFlag，openSetsunaFlag来表示选项对于开启flag的作用，取值和前面三个一样，不多做叙述了。每个Choice要包含两个指针（ 或者也可以是两个序号），分别表示选A和选B（或者判定的是，否）所对应的后一个Choice应该是什么。

现在该说说整体算法设计思路了。我觉得这个问题应该用栈解决，这里我提供两种思路（其实是大同小异）。第一种，选项1的Choice入栈。每次栈顶元素tmp出栈（注意是出栈， 移出去了），然后把它的两个儿子复制之后得到tmpA，tmpB，利用tmp计算出tmpA和tmpB的各项好感度以及flag是否开启，然后将tmpA和tmpB入栈。重复这样做直到栈空。第二种，我这里给Choice添加了一个int变量status，可以取0,1,2分别用来标识它是准备选A选项，还是准备选B选项，还是A，B都选过了。选项1的Choice入栈，每次判断栈顶元素的status，如果是0，代表准备选A，将status加一，然后修改A儿子的各个数值之后将其入栈；如果是1，代表准备选B，status再加一，然后修改B儿子的各个数值之后将其入栈；如果是2，代表A，B都选过了，将其出栈。我个人推荐第二种方法，因为占用空间少，第一种需要复制大量的Choice同时压到栈里，第二个等于只有十几个Choice，我们做的只是在修改它的值而已。至于选项A，B能不能选，就另外加条件判断，这里贴出代码。

#include
#include

using namespace std;

struct Choice {
	Choice* A;
	Choice* B;

	int type;//-1代表结局，0代表正常选项，1代表NE判定，2代表TE判定
	int endingType;//0代表雪菜TE，1代表雪菜NE，2代表冬马NE，3代表冬马TE
	int status;//0代表下一个选A，1代表下一个选B
	int num;//选项序号，用于屏蔽选项

	int weight;

	int kazusa;//冬马好感度
	int setsuna;//雪菜好感度
	int fq;//浮气度

	//增加好感度，0,1,2分别代表不增加，A选项增加，B选项增加
	int deltaKazusa;//冬马好感度+1
	int deltaSetsuna;//雪菜好感度+1
	int deltaFq;//浮气度+1

	bool neFlag;//雪菜NE，冬马NE flag
	bool setsunaFlag;//雪菜TE flag

	//打开flag，0,1,2分别代表不打开，A选项打开，B选项打开
	int openNEFlag;//打开NE flag
	int openSetsunaFlag;//打开雪菜TE flag

	Choice* chooseA(bool weightFlag) {
		A->status = 0;
		if (weightFlag) {
			A->weight = weight;
		}
		else {
			A->weight = weight / 2;
		}

		//冬马好感度+1
		if (deltaKazusa==1) {
			A->kazusa = kazusa + 1;
		}
		else {
			A->kazusa = kazusa;
		}
		//雪菜好感度+1
		if (deltaSetsuna==1) {
			A->setsuna = setsuna + 1;
		}
		else {
			A->setsuna = setsuna;
		}
		//浮气度+1
		if (deltaFq==1) {
			A->fq = fq + 1;
		}
		else {
			A->fq = fq;
		}
		//打开NE flag
		if (openNEFlag==1) {
			A->neFlag = true;
		}
		else {
			A->neFlag = neFlag;
		}

		//打开雪菜TE flag
		if (openSetsunaFlag==1) {
			A->setsunaFlag = true;
		}
		else {
			A->setsunaFlag = setsunaFlag;
		}

		return A;
	}

	Choice* chooseB(bool weightFlag) {
		B->status = 0;
		if (weightFlag) {
			B->weight = weight;
		}
		else {
			B->weight = weight / 2;
		}

		//冬马好感度+1
		if (deltaKazusa==2) {
			B->kazusa = kazusa + 1;
		}
		else {
			B->kazusa = kazusa;
		}
		//雪菜好感度+1
		if (deltaSetsuna==2) {
			B->setsuna = setsuna + 1;
		}
		else {
			B->setsuna = setsuna;
		}
		//浮气度+1
		if (deltaFq==2) {
			B->fq = fq + 1;
		}
		else {
			B->fq = fq;
		}
		//打开NE flag
		if (openNEFlag == 2) {
			B->neFlag = true;
		}
		else {
			B->neFlag = neFlag;
		}

		//打开雪菜TE flag
		if (openSetsunaFlag == 2) {
			B->setsunaFlag = true;
		}
		else {
			B->setsunaFlag = setsunaFlag;
		}

		return B;
	}

	Choice(int dK , int dS , int dF , int oNF,int oSF,Choice* cA,Choice *cB,int n,int t=0,int eT=0) {
		status = 0;
		kazusa = setsuna = fq = 0;
		neFlag = setsunaFlag  = false;
		deltaKazusa = dK;
		deltaSetsuna = dS;
		deltaFq = dF;
		openNEFlag = oNF;
		openSetsunaFlag = oSF;
		A = cA;
		B = cB;
		num = n;
		type = t;
		endingType = eT;
	}
};

int main() {
	int endingNumber = 0;
	int endingTypeNumber[4] = { 0 };
	int endingWeightNumber[4] = { 0 };
	bool flagA, flagB;
	Choice *setsunaTrueEnding = new Choice(0, 0, 0, 0, 0, 0, 0, 0, -1, 0), *setsunaNormalEnding = new Choice(0, 0, 0, 0, 0, 0, 0, 1, -1, 1), *kazusaNormalEnding = new Choice(0, 0, 0, 0, 0, 0, 0, 2, -1, 2), *kazusaTrueEnding = new Choice(0, 0, 0, 0, 0, 0, 0, 3, -1, 3);
	Choice *pd4 = new Choice(0, 0, 0, 0, 0, setsunaTrueEnding, kazusaTrueEnding, 4, 2),
		   *pd3 = new Choice(0, 0, 0, 0, 0, pd4, setsunaNormalEnding, 3, 2);
	Choice *choice14 = new Choice(0, 0, 0, 0, 0, pd3, pd4, 14),
		*choice13 = new Choice(0, 0, 0, 0, 0, kazusaNormalEnding, choice14, 13),
		*choice12 = new Choice(1, 0, 0, 0, 2, choice13, choice13, 12);
	Choice *pd2 = new Choice(0, 0, 0, 0, 0, choice13, choice12, 2, 1);
	Choice *choice11 = new Choice(2, 1, 0, 0, 0, pd2, pd2, 11);
	Choice *pd1 = new Choice(0, 0, 0, 0, 0, choice13, choice11, 1, 1);
	Choice *choice10 = new Choice(1, 0, 2, 0, 0, pd1, pd1, 10),
		*choice9 = new Choice(0, 1, 0, 0, 0, pd1, choice10, 9),
		*choice8 = new Choice(1, 2, 1, 0, 0, choice9, choice9, 8),
		*choice7 = new Choice(0, 1, 2, 0, 0, choice8, choice8, 7),
		*choice6 = new Choice(1, 2, 0, 0, 0, choice7, choice7, 6),
		*choice5 = new Choice(0, 1, 1, 0, 0, choice7, choice6, 5),
		*choice4 = new Choice(2, 0, 1, 0, 0, choice5, choice5, 4),
		*choice3 = new Choice(0, 2, 0, 0, 0, choice4, choice5, 3),
		*choice2 = new Choice(0, 2, 0, 1, 0, choice5, choice3, 2),
		*choice1 = new Choice(0, 1, 0, 0, 0, choice2, choice2, 1);
	choice1->weight = 16384;
	stack choiceStack;
	choiceStack.push(choice1);
	
	while (!choiceStack.empty()) {
		Choice* tmp = choiceStack.top();
		if (tmp->type==0) {
			flagA = false;
			flagB = false;
			if ((tmp->num == 13 && tmp->setsunaFlag) || (tmp->num == 12 && tmp->setsuna > tmp->kazusa + tmp->fq)) {
				flagA = true;
			}
			if (tmp->num == 14 && tmp->kazusa < 6) {
				flagB = true;
			}
			if (tmp->status==0) {
				tmp->status = tmp->status + 1;
				if (flagA) {
					continue;
				}
				choiceStack.push(tmp->chooseA(flagB));
			}
			else if (tmp->status == 1) {
				tmp->status = tmp->status + 1;
				if (flagB) {
					continue;
				}
				choiceStack.push(tmp->chooseB(flagA));
			}
			else {
				choiceStack.pop();
			}
		}
		else if(tmp->type==1){
			choiceStack.pop();
			if (tmp->neFlag) {
				choiceStack.push(tmp->chooseA(true));
			}
			else {
				choiceStack.push(tmp->chooseB(true));
			}
		}
		else if(tmp->type==2){
			choiceStack.pop();
			if (tmp->setsunaFlag) {
				choiceStack.push(tmp->chooseA(true));
			}
			else {
				choiceStack.push(tmp->chooseB(true));
			}
		}
		else if (tmp->type == -1) {
			choiceStack.pop();
			endingNumber++;
			endingTypeNumber[tmp->endingType] = endingTypeNumber[tmp->endingType] + 1;
			endingWeightNumber[tmp->endingType] = endingWeightNumber[tmp->endingType] + tmp->weight;
		}
	}
	cout << "endingNumber:" << endingNumber << endl;
	cout << "雪菜TE：" << endingTypeNumber[0] << endl;
	cout << "雪菜NE：" << endingTypeNumber[1] << endl;
	cout << "冬马NE：" << endingTypeNumber[2] << endl;
	cout << "冬马TE：" << endingWeightNumber[3] << endl;
	cout << "雪菜TE：" << endingWeightNumber[0] << endl;
	cout << "雪菜NE：" << endingWeightNumber[1] << endl;
	cout << "冬马NE：" << endingWeightNumber[2] << endl;
	cout << "冬马TE：" << endingWeightNumber[3] << endl;
	return 0;
}

我们最后计算出雪菜TE总共有432种情况，雪菜NE总共有299种情况，冬马NE总共有299种情况，冬马TE总共有4种情况，全局共有1034种情况。很多人到这里可能松一口气，我们拿各个种类的结局数除以1034不就能得到每个结局出现的概率了吗？

这种想法显然是错误的。我给大家举个例子，我们玩抛硬币游戏，我说给你抛两次，你两次都抛反面算你赢，请问你赢的概率是多少？这个是小学数学对吧，是个人都知道4种 情况所以是1/4。这里我再加个条件，我说你只要抛一到一次正面就算我赢，你不用抛了，那么你赢的概率是多少？这个时候其实只有3种情况，就是1正，1反2正，1反2反，但你肯定不会说1/3吧？因为这三个结果概率并不相等，1正的概率是后面两个的两倍，所以依然是1/4。

那么放到我们这里的问题怎么计算呢？我这里提出一个思路，我加入一个名为权重weight的变量，这个weight的值我们这个Choice底下潜在的能选的值是多少（注意，weight值 不代表真实能选的数量，但是与weight总量的比值依然能反映出该到选项有多大概率），选项1的Choice我给它的weight赋值为16384（2的14次方），每次如果是2选1的选项，A，B两个Choice的权值取为当前Choice的一半；如果是判定，由于判定结果具有唯一性，它的下一个Choice权值不变；如果是两个选项有一个被屏蔽掉，那么余下的那个获得当前Choice的全部权值。然后把每个结局获得的所有weight累加起来，最后再除以16384，就是当前结局的概率。

最后贴出结果：

雪菜TE概率：39.3%

雪菜NE概率：30.3%

冬马NE概率：30.4%

冬马TE概率：0.024%

（以上结果是基于每次都是等概率地选两个选项，如果不是概率那么就要复杂很多）

好了，洋洋洒洒写了这么多，也不知道自己说清楚了没有，有问题欢迎随时和我交流。最后告诉大家，我是雪菜党哦，欢迎大家有空来百度的小木曾雪菜吧坐坐！