LeetCode算法刷题——数组篇
(一). 双指针(快慢指针)
1 .简单篇
1.1 给定一个排序数组,你需要在 原地 删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
def removeDuplicates(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
# n-新数组长度;p-新数组指针,指向新数组最后一个元素;q-旧数组遍历指针
n, p = 1, 0
for q in range(len(nums)):
if not nums[p] == nums[q]:
p += 1
nums[p] = nums[q]
n += 1
return n
1.2 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。(已解,未能做到真正的因地制宜)
def removeElement(self, nums, val):
"""
:type nums: List[int]
:type val: int
:rtype: int
"""
#这里按照第一个例子进行解决,p,n只用一个即可,官方写法
#p = 0
p,n = 0,0
for q in range(len(nums)):
if not nums[q] == val:
nums[p] = nums[q]
#删除下面这行
n += 1
p = p+1
#返回 p
return n
1.3 给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中,使 nums1 成为一个有序数组。初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。你可以假设 nums1 有足够的空间(空间大小大于或等于 m + n)来保存 nums2 中的元素.(未解,思路为双指针逆) (可以将数组合并,然后排序nums1[:] = sorted(nums1[:m] + nums2))
#########双指针(正向)
def merge(self, nums1, m, nums2, n):
"""
:type nums1: List[int]
:type m: int
:type nums2: List[int]
:type n: int
:rtype: None Do not return anything, modify nums1 in-place instead.
"""
# nums1[:] = sorted(nums1[:m] + nums2)
nums1_copy = nums1[:m]
nums1[:] =[]
p1 = 0
p2 = 0
while p1<m and p2<n:
if nums1_copy[p1] < nums2[p2]:
nums1.append(nums1_copy[p1])
p1 = p1 +1
else:
nums1.append(nums2[p2])
p2 = p2 +1
if p1<m:
nums1[p1+p2:] = nums1_copy[p1:]
if p2 < n :
nums1[p1+p2:] = nums2[p2:]
################双指针(逆向)空间复杂度更小
def merge(self, nums1, m, nums2, n):
"""
:type nums1: List[int]
:type m: int
:type nums2: List[int]
:type n: int
:rtype: void Do not return anything, modify nums1 in-place instead.
"""
# two get pointers for nums1 and nums2
p1 = m - 1
p2 = n - 1
# set pointer for nums1
p = m + n - 1
# while there are still elements to compare
while p1 >= 0 and p2 >= 0:
if nums1[p1] < nums2[p2]:
nums1[p] = nums2[p2]
p2 -= 1
else:
nums1[p] = nums1[p1]
p1 -= 1
p -= 1
# add missing elements from nums2
nums1[:p2 + 1] = nums2[:p2 + 1]
1.4 给定一个已按照升序排列 的有序数组,找到两个数使得它们相加之和等于目标数。函数应该返回这两个下标值 index1 和 index2,其中 index1 必须小于 index2。说明:返回的下标值(index1 和 index2)不是从零开始的。你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。(未解,想用二分,可是没写出来,感觉自己脑子里都是灌得都是水)
def twoSum(self, numbers, target):
"""
:type numbers: List[int]
:type target: int
:rtype: List[int]
"""
left = 0
right = len(numbers) -1
while numbers[left] + numbers[right] != target:
if numbers[left] + numbers[right] < target:
left = left +1
else:
right = right-1
return left+1,right+1
二分+双指针
def binary_search(self,num,tar,left,right,if_find_left):
while left<=right:
mid=(left+right)//2
if num[mid]<tar:
left=mid+1
elif num[mid]>tar:
right=mid-1
else:
return mid
return left if if_find_left else right
def twoSum(self, numbers: List[int], target: int) -> List[int]:
l,r=0,len(numbers)-1
while l<r:
sum_=numbers[l]+numbers[r]
if sum_<target:
l=self.binary_search(numbers,target-numbers[r],left=l+1,right=r,if_find_left=True)
elif sum_>target:
r=self.binary_search(numbers,target-numbers[l],left=l,right=r-1,if_find_left=False)
else:
return [l+1,r+1]
2.中等
2.1 给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。说明:你不能倾斜容器,且 n 的值至少为 2。(还是不能理解双指针问题)
def maxArea(self, height):
"""
:type height: List[int]
:rtype: int
"""
low = 0
high = len(height)-1
area = 0
while low<high:
tag_area = min(height[low],height[high])*(high-low)
if area<tag_area:
area = tag_area
if height[low]<height[high]:
low = low+1
else:
high = high -1
return area
(二). 二分查找
1 .简单篇
1.1给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。你可以假设数组中无重复元素。(已解,暴力方法,效率不高;推荐二分查找)
def searchInsert(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
for i in range(len(nums)):
if target ==nums[i] or target < nums[i]:
return i
return len(nums)
二分查找方法(精选中的写法)
def searchInsert(self, nums: List[int], target: int) -> int:
size = len(nums)
if size == 0:
return 0
# 特判
if nums[size - 1] < target:
return size
left = 0
right = size - 1
while left < right:
mid = left + (right - left) // 2
# 严格小于 target 的元素一定不是解
if nums[mid] < target:
# 下一轮搜索区间是 [mid + 1, right]
left = mid + 1
else:
right = mid
return left
(三). 动态规划

1 .简单篇
1.1 给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。(未解)
写法一
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
for i in range(1, len(nums)):
nums[i]= nums[i] + max(nums[i-1], 0)
return max(nums)
写法二
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
if len(nums) == 0:
return 0
if len(nums) == 1:
return nums[0]
# 下面为nums长度至少为2的情况
res = nums[0] # 先设定一个初始值(假设第一个数是可获得的最小值)
for i in range(1, len(nums)):
nums[i] = max(nums[i], nums[i] + nums[i - 1]) # 更新后的nums[i]存储 以原始num[i]为结尾的子数组和的最大值
res = max(res, nums[i]) # 更新最大值
return res
1.2 (已解,进一步清晰动态规划,当前一步依附于前一步计算的结果)
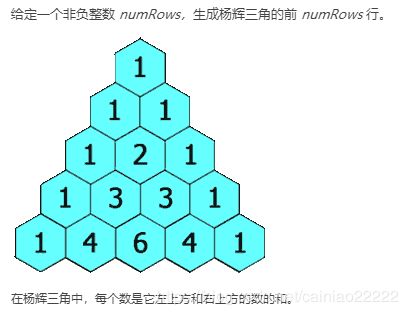
def generate(self, numRows):
"""
:type numRows: int
:rtype: List[List[int]]
"""
nums =[]
for i in range(1,numRows+1):
tag = [1]*i
nums.append(tag)
if numRows<3:
return nums
for i in range(2,numRows):
list_last = []
for k in range(len(nums[i-1])-1):
nums[i][k+1] = nums[i-1][k] +nums[i-1][k+1]
return nums
1.3 给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票一次),设计一个算法来计算你所能获取的最大利润。注意:你不能在买入股票前卖出股票。(已解,暴力求解。总是无法看出用什么方法解题,看不出要用动态规划,还是要多多做题,思考,理解)
暴力解法
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
if len(prices) == 0:
return 0
maxprices = 0
for i in range(len(prices)-1):
for j in range(i,len(prices)-1):
tag = prices[j+1] - prices[i]
maxprices = max(maxprices,tag)
return maxprices
动态规划
#动态规划
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
if len(prices) == 0:
return 0
min_prices = prices[0]
max_prices = 0
dp = [0]*len(prices)
for i in range(1,len(prices)):
min_prices = min(min_prices,prices[i])
dp[i] = max(dp[i-1],prices[i]-min_prices)
return dp[-1]
#动态规划进一步简化
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
if len(prices) == 0:
return 0
min_prices = prices[0]
max_prices = 0
for i in range(1,len(prices)):
min_prices = min(min_prices,prices[i])
max_prices = max(max_prices,prices[i]-min_prices)
return max_prices
1.4 给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。(未解)
动态规划
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
lens = len(prices)
if lens<2:
return 0
on = [0]*lens
off = [0]*lens
on[0] = -prices[0]
off[0] = 0
for i in range(1,lens):
on[i] = max(on[i-1],off[i-1] - prices[i])
off[i] = max(off[i-1],on[i-1]+prices[i])
return off[lens-1]
贪心
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
res = 0;
lens = len(prices)
for i in range(lens-1):
tag = prices[i + 1] - prices[i];
if (tag > 0) :
res += tag;
return res;
(四). 摩尔投票法

1 .简单篇
1.1给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。你可以假设数组是非空的,并且给定的数组总是存在多数元素。(已解,方法较多)
官方解题
class Solution:
def majorityElement(self, nums):
count = 0
candidate = None
for num in nums:
if count == 0:
candidate = num
count += (1 if num == candidate else -1)
return candidate