12-PCA和GridSearchCV的简单介绍及使用

tags: python,机器学习,svm,PCA,GridSearchCV,SMOTE

PCA 计算原理

PCA使用背景

在许多领域的研究与应用中，往往需要对反映事物的多个变量进行大量的观测，收集大量数据以便进行分析寻找规律。多变量大样本无疑会为研究和应用提供了丰富的信息，但也在一定程度上增加了数据采集的工作量，更重要的是在多数情况下，许多变量之间可能存在相关性，从而增加了问题分析的复杂性，同时对分析带来不便。如果分别对每个指标进行分析，分析往往是孤立的，而不是综合的。盲目减少指标会损失很多信息，容易产生错误的结论。

因此需要找到一个合理的方法，在减少需要分析的指标同时，尽量减少原指标包含信息的损失，以达到对所收集数据进行全面分析的目的。由于各变量间存在一定的相关关系，因此有可能用较少的综合指标分别综合存在于各变量中的各类信息。主成分分析（PCA，Principal Component Analysis）就属于这类降维的方法。

PCA计算

使用sklearn中的PCA函数计算

函数原型及参数说明

这里只挑几个比较重要的参数进行说明。
sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)

• n_components: int, float, None 或 string，PCA算法中所要保留的主成分个数，也即保留下来的特征个数，如果 n_components = 1，将只保留一个特征（数据只保留一列）。如果n_components = 0.95，则保留特征中最重要的前95%；
  如果赋值为string，如n_components='mle'，将自动选取特征个数，使得满足所要求的方差百分比；
  如果没有赋值，默认为None，特征个数不会改变（特征数据本身会改变）。
• copy：True 或False，默认为True，即是否需要将原始训练数据复制。
• whiten：True 或False，默认为False，即是否白化，使得每个特征具有相同的方差，一般选择True效果会好一点。

PCA对象的属性

• explained_variance_ratio_：返回所保留各个特征的方差百分比，如果n_components没有赋值，则所有特征都会返回一个数值且解释方差之和等于1。
• n_components_：返回所保留的特征个数。

PCA常用方法

• fit(X): 用数据X来训练PCA模型。
• fit_transform(X)：用X来训练PCA模型，同时返回降维后的数据。
• inverse_transform(newData) ：将降维后的数据转换成原始数据，但可能不会完全一样，会有些许差别。
• transform(X)：将数据X转换成降维后的数据，当模型训练好后，对于新输入的数据，也可以用transform方法来降维。

对鸢尾花数据进行pca运算

from sklearn.datasets import load_iris

iris = load_iris()
X = iris['data']
y = iris['target']
pca = PCA(n_components=0.95,whiten=True)

X_pca = pca.fit_transform(X)

直接计算方式

计算步骤：

1. 去中心化
2. 协方差
3. 协方差的特征值和特征向量计算
4. 根据特征值占比或者给定的特征值个数，选出该特征值对应的特征向量
5. 使用选取出来的特征向量和原始数据进行矩阵运算

读取鸢尾花数据

from sklearn.datasets import load_iris

iris = load_iris()
X = iris['data']
y = iris['target']

去重心化

# 1. 去中心化
A = X - X.mean(axis=0)

协方差

# 2. 协方差
V = np.cov(A, rowvar=False)

特征值和特征向量计算

# 3. 特征值和特征向量计算
T, TV = np.linalg.eig(V)
display(T, TV)

求取结果：

array([4.22824171, 0.24267075, 0.0782095 , 0.02383509])
array([[ 0.36138659, -0.65658877, -0.58202985,  0.31548719],
       [-0.08452251, -0.73016143,  0.59791083, -0.3197231 ],
       [ 0.85667061,  0.17337266,  0.07623608, -0.47983899],
       [ 0.3582892 ,  0.07548102,  0.54583143,  0.75365743]])

验证求取的向量V特征值和特征向量是否正确

从数学上看如果向量$v$与矩阵M满足$Mv=\lambda v$，则称向量$v$是矩阵$M$的一个特征向量，$\lambda$是对应的特征值。
这一等式被称为特征值方程。

# 按列取
n1 = np.dot(V, TV[:,0])
n2 = np.dot(T[0],TV[:,0])
print(n1,n2)

输出结果为：

array([ 1.52802986, -0.35738162,  3.62221038,  1.51493333])
array([ 1.52802986, -0.35738162,  3.62221038,  1.51493333])

根据比例选择特征值对应的特征向量

由于需要和上面使用pca函数计算的结果做对比，所以这里也选取95%的特征。

# 求特征值占比
T.cumsum()/T.sum()
# 这里的数据说明了为什么上面给n_components=0.95时，选出来两个特征，因为第一个属性只占了0.92，所以需要继续添加属性
# 添加到第二个属性之后，占比为0.98，满足条件，所以最后选出来两个特征

输出结果：

array([0.92461872, 0.97768521, 0.99478782, 1.        ])

由上面的计算结果可以看出，选择前两个特征即可。

# 4. 根据特征值占比大于95%的情况，选出该特征值对应的特征向量
# 这里是第0列和第1列
P = TV[:,(0,1)]

使用选取出来的特征向量和原始数据进行矩阵运算

from sklearn.preprocessing import StandardScaler

s = StandardScaler()
s.fit_transform(np.dot(X, P))

最后发现计算的结果和直接使用pca计算的结果基本相等，只有某列和pca计算的值符号相反，这是由于求特征相量时计算出现的。

pca降维对手写数字数据进行训练

获取手写数字数据

digits = pd.read_csv('./digits.csv')
digits

data = digits.iloc[:,1:]
target = digits.iloc[:,0]

检查数据中第一列所有的值

print(data.iloc[:,1].unique())
# 发现数据中第一列全是零
# 对系统计算而言，没有任何有用作用

对于这种数据量很大(42000行)，特征数又多(784个)，如果直接使用SVC进行分类，则会导致计算量太大，更不用说再和网格交叉验证一起使用了。而且上面的代码验证数据中第一行全是零，也就是方差为0，这种数据对模型训练没有任何有用作用。
所以上面的数据需要使用pca进行降维。

pca运算并计算得分

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(data,target)
from sklearn.decomposition import PCA

# 从原来个784变为30，这里可以理解为从原来的784个特征中，计算选取30个最能代表原来数据特征的数据出来
pca = PCA(n_components=30, whiten=True)
X_train_pca = pca.fit_transform(X_train)

from sklearn.svm import SVC

svc = SVC()
svc.fit(X_train_pca, y_train)
# 可以发现降维了之后，训练模型花费的时间远小于不降维的情况

score1 = svc.score(X_train_pca, y_train)
print(score1)

X_test_pca = pca.transform(X_test)
score2 = svc.score(X_test_pca, y_test)
print(score2)

上面的得分为：score1为0.9892698412698413，score2为0.9787619047619047。

一般都图片处理时，会使用pca降维。
另外数据需要隐藏其原始内容时(脱敏处理)，也可以使用pca降维，因为这样操作之后，得到的时候就和之前的完全不同了，不能看出降维后数据的意义。
缺点：pca降维之后，数据失去了他的物理意义

pca降维对人脸数据进行训练

获取人脸数据

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.decomposition import PCA
from sklearn.svm import SVC

# min_faces_per_person 数据库中某个人物中最小的个数
# 如果数目小于该数，则不会被选择。
faces = fetch_lfw_people(min_faces_per_person=70, resize=1)

data = faces['data']
target = faces['target']
target_name = faces['target_names']
print(data.shape)

上面打印的结果为数据的形状：(1288, 11750)，可以看到，数据有11750个特征，直接使用原始数据进行训练，非常耗时。

查看数据各类个数

from pandas import Series,DataFrame
y_s = Series(data=target)
y_c = y_s.value_counts()
dd = DataFrame(data={'name': target_name[y_c.index], 'counts': y_c})
dd

	name	counts
3	George W Bush	530
1	Colin Powell	236
6	Tony Blair	144
2	Donald Rumsfeld	121
4	Gerhard Schroeder	109
0	Ariel Sharon	77
5	Hugo Chavez	71

通过上面表格中的数据，可以看出，上面的样本不均衡。

获取训练数据

X_train, X_test, y_train, y_test =train_test_split(data, target,test_size=96)

pca = PCA(n_components=30, whiten=True)
X_train_pca = pca.fit_transform(X_train)
print(X_train_pca.shape)

上面打印的结果为：(1192, 30)

fit_transform是fit和transform的结合
Note:

1. 必须先用fit_transform(trainData)，之后再transform(testData)
2. 如果直接transform(testData)，程序会报错
3. 如果fit_transfrom(trainData)后，使用fit_transform(testData)而不transform(testData)，虽然也能归一化，但是两个结果不是在同一个“标准”下的，具有明显差异。(一定要避免这种情况)

使用GridSearchCV网格搜索和交叉验证选取最优参数

GridSearchCV()函数中部分参数含义：

• estimator: 需要调整参数的模型的对象
• param_grid：需要调整的参数，以字典的形式写。其中字典的键即要调整的参数名，一定要和调参模型中的参数名一致
• cv: cross validation 交叉验证,cv的值即为训练数据分的段数。比如c=3，则训练数据被分为3份，假设为A、B、C，则其会先A+B做训练数据，C做测试数据，然后能得到一个模型及得分，然后为A+C,B B+C,A，最后对于分类模型则取平均得分，回归模型则进行投票。这样就能消除一下因为取数据不同，造成得分不同的影响。
• n_jobs: 如果训练数据比较大的时候，可以将该参数赋值，这样就可以使用多进程进行训练，提高计算速度。其值为-1时，代表使用所有线程。

选取最优参数

svc = SVC()
param_grid = {
    'C': [0.01, 0.1, 1, 10, 100],
    'gamma': [0.003, 0.03, 0.3, 3, 33]
}
gv = GridSearchCV(estimator=svc, param_grid=param_grid, n_jobs=4, cv=5)

gv.fit(X_train_pca, y_train)
print(gv.best_params_)
print(gv.best_score_)

X_test_pca = pca.transform(X_test)

print(gv.score(X_test_pca, y_test))

上面的输出结果为：
gv.best_params_：{‘C’: 10, ‘gamma’: 0.03}
gv.best_score_：0.7944692521360007
gv.score(X_test_pca, y_test)：0.7604166666666666

对预测结果进行可视化

plt.figure(figsize=(6*3,8*4.5))
for i in range(48):
    plt.subplot(8,6,i+1)
    plt.imshow(X_test[i*2].reshape(*images[0].shape), cmap='gray')
    if y_[i*2] != y_test[i*2]:
        c = 'r'
    else:
        c = 'k'
    plt.title(f'True:{target_name[y_test[i*2]].split()[-1]}\nPredict:{target_name[y_[i*2]].split()[-1]}',c=c)
    plt.axis('off')

从上面的模型得分可以看出，上面预测的结果并不是很好，这主要是因为样本数据中，各类别数量不均衡导致的，其中数量最多的是George W Bush，有530个，而最少的为：Hugo Chavez，有71个。对于这样的样本，可以使用一定的方式进行处理来提高其预测准确率。

使用过采样SMOTE的方法提高人脸识别准确率

获取人脸数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.svm import SVC
import sklearn.datasets as datasets

faces = datasets.fetch_lfw_people(min_faces_per_person=70,resize=1)

X = faces['data']
y = faces['target']
names = faces['target_names']

对比使用pca降维前后模型的运算时间

不使用pca降维

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2, random_state=1)
svc = SVC(kernel='rbf')

计算运行时间：

%%time
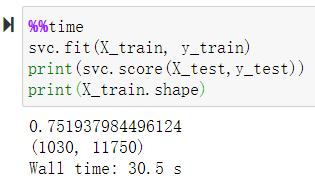
svc.fit(X_train, y_train)
print(svc.score(X_test,y_test))
print(X_train.shape)

运算时间和模型得分及训练数据尺寸为：Wall time: 30.5 s，0.751937984496124，(1030, 11750)

使用pca降维

from sklearn.decomposition import PCA
# 主成分分析，重要的属性留下，不重要的属性抛弃
# n_components为需要保留代属性个数（为小数时代表占总体的比例）
# whiten白化，就是归一化处理 
pca = PCA(n_components=0.8,whiten=True)
# 转换后的数据可以代表原来的数据，但是转换后的数据的属性就没有实际的意义了，该过程也被称作脱敏处理
X_pca = pca.fit_transform(X)

X_train, X_test, y_train, y_test = train_test_split(X_pca,y,test_size=0.2,random_state=1)
svc = SVC()

计算运行时间：

%%time
svc.fit(X_train, y_train)
print(svc.score(X_test, y_test))
print(X_train.shape)

同样输出结果为：0.8178294573643411，Wall time: 188 ms，(1030, 44)

通过上面代码运行结果可以发现，使用pca降维，极大的降低了运行时间（使用前30.5s，使用后188ms，大概相差162倍），且对模型预测结果有所提升。这里为了使用同样的测试数据，在train_test_split函数中，指定了random_state=1，所以取出的数据一致。

SMOTE过采样均衡样本数据

# 过采样
from imblearn.over_sampling import SMOTE

smote = SMOTE()
X2, y2 = smote.fit_resample(X,y)

y_s2 = Series(data=y2)
y_c2 = y_s2.value_counts()
dd = DataFrame(data={'name': names[y_c2.index], 'counts': y_c2})
dd

	name	counts
5	Hugo Chavez	530
3	George W Bush	530
1	Colin Powell	530
6	Tony Blair	530
4	Gerhard Schroeder	530
2	Donald Rumsfeld	530
0	Ariel Sharon	530

通过输出SMOTE过采样后的样本各类个数可以看出，操作后的样本很均衡。

pca降维并训练模型

pca = PCA(n_components=0.9,whiten=True)

X2_pca = pca.fit_transform(X2)
print(X2_pca.shape)

输出结果为：(3710, 100)

face_train, face_test, X_train, X_test, y_train, y_test = train_test_split(X2, X2_pca,y2,test_size=0.2)

svc = SVC()
svc.fit(X_train, y_train)
print(svc.score(X_train, y_train))
print(svc.score(X_test, y_test))

训练数据得分和预测数据得分：0.9993261455525606，0.9878706199460916

模型预测结果可视化

y_ = svc.predict(X_test)

plt.figure(figsize=(10*2,10*3))
for i in range(100):
    plt.subplot(10,10,i+1)
    face = face_test[i].reshape(125,94)
    plt.imshow(face, cmap='gray')
    if y_[i] == y_test[i]:
        plt.title(f'True:{names[y_test[i]].split(" ")[-1]}\nPredct:{names[y_[i]].split(" ")[-1]}')
    else:
        plt.title(f'True:{names[y_test[i]].split(" ")[-1]}\nPredct:{names[y_[i]].split(" ")[-1]}', c='r')
        
    plt.axis('off')