算法竞赛入门经典--训练指南 笔记
P1(贪心)
自己想的糟糕的算法:
#include//从大到小排序龙头和骑士,每个龙头由“恰好”能砍掉的骑士来砍
#include//貌似没问题,但是又难写又慢
#include//就当复习stl了
#include
using namespace std;
int n=1,m=1;
int a[30000];
vector b;
vector::iterator iter;
bool boo[30000];
int b1;
bool cmp(int x,int y)
{
if(x>=y) return true;
else return false;
}
int main()
{
int i,j,t,ans;
bool flag;
do
{
scanf("%d%d",&n,&m);
if(n==0&&m==0)
break;
b.clear();
memset(a,0,sizeof(a));
for(i=0;im)
{
printf("Loowater is doomed!\n");
continue;
}
flag=false;
ans=0;
sort(a,a+n,cmp);
sort(b.begin(),b.end());
for(i=0;i #include//从小到大排序龙头和骑士,每个骑士砍对应龙头,如果砍不了就换成下一个,直到能砍了或骑士用完了为止
#include
using namespace std;
const int maxn=20005;
int a[maxn],b[maxn];
int main()
{
int n,m;
while(scanf("%d%d",&n,&m)==2&&n&&m)
{
for(int i=0;i=a[cur])
{
cost+=b[i];
if(++cur==n) break;
}
if(cur P2(贪心)
首先是直觉给出算法:
猜想1:
执行时间长的先交代。
猜想2:
交代时间长的先交代。
然后是证明与完善:
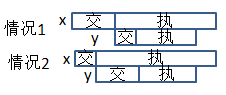
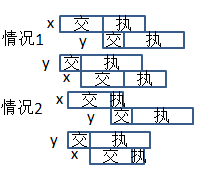
考虑有相邻执行的两个任务x和y,现在要确定它们的顺序,显然它们的顺序不会影响其它任务的完成时间。
①当它们执行时间一样长时,不论交代时间关系如何,显然顺序并不影响完成时间。
由此,猜想2被否决。
并且,对于猜想1得到了完善:执行时间一样长时先后顺序任意。
②当它们执行时间不一样长时:不妨设交换前先交代x。
A.交换前x比y后结束。
显然,无论交代时间关系如何,交换它们只能让完成时间更长。
B.交换前x比y先结束。
显然,交换前总时间是x交+y交+y执,交换后是y交+max(y执,x交+x执)
那么何时交换后能使时间变短呢?(如果说交换后时间变短,也就是说交换后的顺序更好)
情况1:y执行 那么,交换后是y交+x交+x执 如果使时间变短,则x交+y交+y执>y交+x交+x执,即(x交+y交+y执)-(y交+x交+x执)>0,所以y执>x执 情况2:y执>=x交+x执 那么,交换前总时间是x交+y交+y执,交换后是y交+y执,显然时间变短,而此时显然y执>x执 综上所述,如果y执行时间更长,就应交换x和y的顺序,使y先执行,也就是执行时间长的应该先执行。 (只列出x交代时间较长的情况,x交代时间较短也是类似的) P4 首先,举个例子,1号给了2号1个金币,2号给了1号3个,可以简化为2号给1号2个金币。 因此,把两个人间金币的交换简化为单方向的给金币。 xi表示第i个人给了第i-1个人xi个金币(2<=i<=n) (x1表示第1个人给了第n个人x1个金币)(如果xi为负则表示第i-1个人给了第i个人-xi个金币)。 Ai表示第i个人原有金币。M表示每个人最后应有的金币。 可以列出方程M=A1-x1+x2=A2-x2+x3=A3-x3+x4=... 则对于式1,x2=M-A1+x1 对于式2,M=A2-M+A1-x1+x3,x3=2M-A1-A2+x1=(M-A1)+(M-A2)+x1 对于式3,M=A3-2M+A1+A2-x1+x4,x4=3M-A1-A2-A3+x1=(M-A1)+(M-A2)+(M-A3)+x1 ..... 定义Ci=(A1+A2+...+Ai)-i*M 则x2=x1-C1 x3=x1-C2 x4=x1-C3 ...... xn=x1-C(n-1) 现在,我们要求|x1|+|x2|+...+|xn|的最小值 就是|x1|+|x1-C1|+|x1-C2|+...+|xn-C(n-1)|的最小值 而C1到C(n-1)的值都是已经确定的,因此现在就是在数轴上找一个点到0,C1,C2,...,C(n-1)的距离之和最小 可以证明,当这个点对应的数是0,C1,C2,...,C(n-1)的中位数时距离之和最小。 怎么证明//http://www.cnblogs.com/hsiaonan/articles/5041630.html快速选择,中位数BFPRT
//http://www.cnblogs.com/hibernate6/archive/2011/05/19/2522294.html-SELECT
#include