漫画算法小灰学习算法笔记

 

写在前面的话：

学习算法，需要做的是领悟算法思想、理解算法对内存空间和性能的
影响，以及开动脑筋去寻求解决问题的最佳方案。

 

正文如下：

第1章 算法概述

1.1.2 什么是算法

算出1+2+3+4+5+6+7……一直加到10000的结果，算不完不许回家！

(1+10 000)×10 000 ÷ 2 = 50 005 000

所采用的这种等差数列求和的方法，被称为高斯算法。

在数学领域里，算法是用于解决某一类问题的公式和思想。

计算机科学领域的算法，它的本质是一系列程序指令，用于解决特定的

运算和逻辑问题

算法有简单的，也有复杂的。
简单的算法，诸如给出一组整数，找出其中最大的数。

复杂的算法，诸如在多种物品里选择装入背包的物品，使背包里的物品
总价值最大，或找出从一个城市到另一个城市的最短路线

算法有高效的，也有拙劣的

刚才所讲的从1加到10000的故事中，高斯所用的算法显然是更加高效的
算法，它利用等差数列的规律，四两拨千斤，省时省力地求出了最终结
果。
而老师心中所想的算法，按部就班地一个数一个数进行累加，则是一种
低效、笨拙的算法。虽然这种算法也能得到最终结果，但是其计算过程
要低效得多。

在计算机领域，我们同样会遇到各种高效和拙劣的算法。衡量算法好坏
的重要标准有两个。
时间复杂度
空间复杂度

 

1.1.3 什么是数据结构

数据结构是算法的基石。如果把算法
比喻成美丽灵动的舞者，那么数据结构就是舞者脚下广阔而坚实的
舞台。

数据结构，对应的英文单词是data structure ，是数据的组织、管理和
存储格式，其使用目的是为了高效地访问和修改数据。
数据结构都有哪些组成方式呢？

1. 线性结构
线性结构是最简单的数据结构，包括数组、链表，以及由它们衍生出来
的栈、队列、哈希表。

2. 树
树是相对复杂的数据结构，其中比较有代表性的是二叉树，由它又衍生
出了二叉堆之类的数据结构。

3. 图
图是更为复杂的数据结构，因为在图中会呈现出多对多的关联关系

关于算法在不同数据结构上的操作过程，在后续的章节中我们会一一进
行学习。

 

1.2.1 算法的好与坏

时间复杂度和空间复杂度究竟是什么呢？首先，让我们来想象一个场
景。

某一天，小灰和大黄同时加入了同一家公司

一天后，小灰和大黄交付了各自的代码，两人的代码实现的功能差不
多。
大黄的代码运行一次要花100ms ，占用内存5MB 。
小灰的代码运行一次要花100s ，占用内存500MB 。

于是……

 

在上述场景中，小灰虽然也按照老板的要求实现了功能，但他的代码存
在两个很严重的问题。
1. 运行时间长
运行别人的代码只要100ms，而运行小灰的代码则要100s，使用者肯定
是无法忍受的。
2. 占用空间大
别人的代码只消耗5MB的内存，而小灰的代码却要消耗500MB的内存，
这会给使用者造成很多麻烦。

由此可见，运行时间的长短和占用内存空间的大小，是衡量程序好坏的
重要因素。

 

可是，如果代码都还没有运行，
我怎么能预知代码运行所花的时间呢？

由于受运行环境和输入规模的影响，
代码的绝对执行时间是无法预估的。但我们却可以预估代码的基本
操作执行次数。

 

1.2.2 基本操作执行次数

关于代码的基本操作执行次数：

设T(n)为程序基本操作执行次数的函数（也可以认
为是程序的相对执行时间函数）n为输入规模

场景1 　T(n) = 3n，执行次数3n是线性 的。
1. void eat1(int n){
2. for(int i=0; i 3. System.out.println("等待1分钟");
4. System.out.println("等待1分钟");
5. System.out.println("吃1cm 面包");
6. }
7. }
场景2 　T(n) = 5logn，执行次数是用对数 计算的。
1. void eat2(int n){
2. for(int i=n; i>1; i/=2){
3. System.out.println("等待1分钟");
4. System.out.println("等待1分钟");
5. System.out.println("等待1分钟");
6. System.out.println("等待1分钟");
7. System.out.println("吃一半面包");
8. }
9. }
场景3 　T(n) = 2，执行次数是常量 。
1. void eat3(int n){
2. System.out.println(" 等待1分钟");
3. System.out.println(" 吃1个鸡腿");
4. }
场景4 　T(n) = 0.5n^2 + 0.5n，执行次数是用多项式 0.5n^2 + 0.5n计算的。
1. void eat4(int n){
2. for(int i=0; i 3. for(int j=0; j 4. System.out.println("等待1分钟");
5. }
6. System.out.println("吃1cm 面包");
7. }
8. }

 

1.2.3 渐进时间复杂度

有了基本操作执行次数的函数T(n)，是否就可以分析和比较代码的运行
时间了呢？还是有一定困难的。
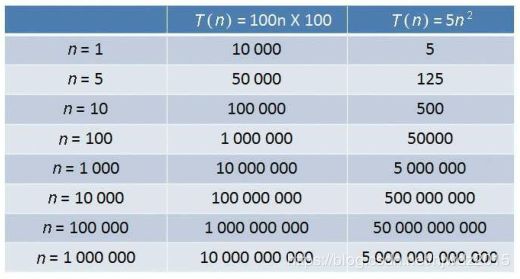
例如算法A的执行次数是T(n)= 100n，算法B的执行次数是T(n)= 5n^2 ，这
两个到底谁的运行时间更长一些呢？这就要看n的取值了

因此，为了解决时间分析的难题，有了渐进时间复杂度（asymptotic
time complexity） 的概念，其官方定义如下。
若存在函数f(n)，使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于
零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))，称为
O(f(n))，O为算法的渐进时间复杂度，简称为时间复杂度。
因为渐进时间复杂度用大写O来表示，所以也被称为大O表示法 。

这个定义好晦涩呀，看不明白。

直白地讲，时间复杂度就是把程序的
相对执行时间函数T(n)简化为一个数量级，这个数量级可以是n、n^2
、n^3 等。

如何推导出时间复杂度呢？有如下几个原则。
如果运行时间是常数量级，则用常数1表示
只保留时间函数中的最高阶项
如果最高阶项存在，则省去最高阶项前面的系数
让我们回头看看刚才的4个场景。
场景1
T(n) = 3n，
最高阶项为3n，省去系数3，则转化的时间复杂度为：T(n)=O(n) 。

场景2
T(n) = 5logn，
最高阶项为5logn，省去系数5，则转化的时间复杂度为：T(n) =O(logn)
。

场景3
T(n) = 2，
只有常数量级，则转化的时间复杂度为：T(n) =O(1) 。

场景4
T(n) = 0.5n 2 + 0.5n，
最高阶项为0.5n 2 ，省去系数0.5，则转化的时间复杂度为：T(n) =O(n
2  )

这4种时间复杂度究竟谁的程度执行用时更长，谁更节省时间呢？当n的
取值足够大时，不难得出下面的结论：
O(1)

 

1.2.4 时间复杂度的巨大差异

大黄，我还有一个问题，现在计
算机硬件的性能越来越强了，我们为什么还这么重视时间复杂度
呢？
问得很好，让我们用两个算法来做一
个对比，看一看高效算法和低效算法有多大的差距。

算法A的执行次数是T(n)= 100n，时间复杂度是O(n)。
算法B的执行次数是T(n)= 5n^2 ，时间复杂度是O(n^2 )。

算法A运行在小灰家里的老旧电脑上，算法B运行在某台超级计算机
上，超级计算机的运行速度是老旧电脑的100倍。

那么，随着输入规模n的增长，两种算法谁运行速度更快呢？

从上面的表格可以看出，当n的值很小时，算法A的运行用时要远大于
算法B；当n的值在1000左右时，算法A和算法B的运行时间已经比较接
近；随着n的值越来越大，甚至达到十万、百万时，算法A的优势开始
显现出来，算法B的运行速度则越来越慢，差距越来越明显。
这就是不同时间复杂度带来的差距。

要想学好算法，就必须理解时间复杂
度这个重要的基础概念。有关时间复杂度的知识就介绍到这里，我
们下一节再见！

 

1.3 空间复杂度

1.3.1 什么是空间复杂度

 

在运行一段程序时，我们不仅要执行各种运算指令，同时也会根据需
要，存储一些临时的中间数据  ，以便后续指令可以更方便地继续执
行。

但是，内存空间是有限的，在时间复杂度相同的情况下，算法占用的内
存空间自然是越小越好。如何描述一个算法占用的内存空间的大小呢？
这就用到了算法的另一个重要指标——空间复杂度（space
complexity） 。

和时间复杂度类似，空间复杂度是对一个算法在运行过程中临时占用存
储空间大小的量度，它同样使用了大O表示法。

程序占用空间大小的计算公式记作S(n)=O(f(n)) ，其中n为问题的规模，
f(n)为算法所占存储空间的函数。

 

1.3.2 空间复杂度的计算

基本的概念已经明白了，那么，
我们如何来计算空间复杂度呢？
具体情况要具体分析。和时间复杂度
类似，空间复杂度也有几种不同的增长趋势。
常见的空间复杂度有下面几种情形

1. 常量空间
当算法的存储空间大小固定，和输入规模没有直接的关系时，空间复杂
度记作O(1) 。例如下面这段程序：
1. void fun1(int n){
2. int var = 3;
3. …
4. }

2. 线性空间
当算法分配的空间是一个线性的集合（如数组），并且集合大小和输入
规模n成正比时，空间复杂度记作O(n) 。
例如下面这段程序：
1. void fun2(int n){
2. int[] array = new int[n];
3. …
4. }

3. 二维空间
当算法分配的空间是一个二维数组集合，并且集合的长度和宽度都与输
入规模n成正比时，空间复杂度记作O(n 2  ) 。
例如下面这段程序：
1. void fun3(int n){
2. int[][] matrix = new int[n][n];
3. …
4. }

 

4. 递归空间

.....

 

1.3.3 时间与空间的取舍

人们之所以花大力气去评估算法的时间复杂度和空间复杂度，其根本原
因是计算机的运算速度和空间资源是有限的。
就如一个大财主，基本不必为日常花销伤脑筋；而一个没多少积蓄的普
通人，则不得不为日常花销精打细算。

对于计算机系统来说也是如此。虽然目前计算机的CPU处理速度不断飙
升，内存和硬盘空间也越来越大，但是面对庞大而复杂的数据和业务，
我们仍然要精打细算，选择最有效的利用方式。
但是，正所谓鱼和熊掌不可兼得。很多时候，我们不得不在时间复杂度
和空间复杂度之间进行取舍。

在1.3.1小节寻找重复整数的例子中，双重循环的时间复杂度是O(n^2
)，
空间复杂度是O(1)，这属于牺牲时间来换取空间 的情况。

相反，字典法的空间复杂度是O(n)，时间复杂度是O(n)，这属于牺牲空
间来换取时间 的情况。

在绝大多数时候，时间复杂度更为重要一些，我们宁可多分配一些内存
空间，也要提升程序的执行速度。

此外，说起空间复杂度就离不开数据结构。在本章中，我们提及散列
表、数组、二维数组这些常用的集合。如果大家对这些数据结构不是很
了解，可以仔细看看本书第2章关于基本数据结构 的内容，里面有详细
的介绍。

关于空间复杂度的知识，我们就介绍
到这里。时间复杂度和空间复杂度都是学好算法的重要前提，一定
要牢牢掌握哦！

1.4 小结

什么是算法
在计算机领域里，算法是一系列程序指令，用于处理特定的运算和逻辑
问题。
衡量算法优劣的主要标准是时间复杂度和空间复杂度。

 

什么是数据结构
数据结构是数据的组织、管理和存储格式，其使用目的是为了高效地访
问和修改数据。
数据结构包含数组、链表这样的线性数据结构，也包含树、图这样的复
杂数据结构。

什么是时间复杂度
时间复杂度是对一个算法运行时间长短的量度，用大O表示，记作
T(n)=O(f(n))。
常见的时间复杂度按照从低到高的顺序，包括O(1)、O(logn)、O(n)、
O(nlogn)、O(n^2 )等

什么是空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度，
用大O表示，记作S(n)=O(f(n))。
常见的空间复杂度按照从低到高的顺序，包括O(1)、O(n)、O(n^2 )等。其
中递归算法的空间复杂度和递归深度成正比。

 

第2章 数据结构基础

2.1.1 初识数组

有一个数据结构就像军队一样整
齐、有序，这个数据结构叫作数组。

什么是数组？
数组对应的英文是array，是有限个相同类型的变量所组成的有序集合，
数组中的每一个变量被称为元素。数组是最为简单、最为常用的数据结
构。

数组的另一个特点，是在内存中顺序存储  ，因此可以很好地实现逻辑
上的顺序表 。

数组在内存中的顺序存储，具体是什么样子呢？

内存是由一个个连续的内存单元组成的，每一个内存单元都有自己的地
址。在这些内存单元中，有些被其他数据占用了，有些是空闲的。

数组中的每一个元素，都存储在小小的内存单元中，并且元素之间紧密
排列，既不能打乱元素的存储顺序，也不能跳过某个存储单元进行存
储。

2.1.2 数组的基本操作

1. 读取元素
对于数组来说，读取元素是最简单的操作。由于数组在内存中顺序存
储，所以只要给出一个数组下标，就可以读取到对应的数组元素。
假设有一个名称为array的数组，我们要读取数组下标为3的元素，就写
作array[3]；读取数组下标为5的元素，就写作array[5]。需要注意的是，
输入的下标必须在数组的长度范围之内，否则会出现数组越界。
像这种根据下标读取元素的方式叫作随机读取 。

2. 更新元素
要把数组中某一个元素的值替换为一个新值，也是非常简单的操作。直
接利用数组下标，就可以把新值赋给该元素。

2.2 什么是链表

2.2.1 “正规军”和“地下党”

地下党都是一些什么样的人物呢？
在影视作品中，我们可能都见到过地下工作者的经典话语：
“上级的姓名、住址，我知道，下级的姓名、住址，我也知道，但是这
些都是我们党的秘密，不能告诉你们！”

地下党借助这种单线联络的方式，灵活隐秘地传递着各种重要信息。
在计算机科学领域里，有一种数据结构也恰恰具备这样的特征，这种数
据结构就是链表 。
链表是什么样子的？为什么说它像地下党呢？
让我们来看一看单向 链表的结构。

链表（linked list）是一种在物理上非连续、非顺序的数据结构，由若干
节点（node）所组成。

单向 链表的每一个节点又包含两部分，一部分是存放数据的变量data，
另一部分是指向下一个节点的指针next。

链表的第1个节点被称为头节点，最后1个节点被称为尾节点，尾节点的
next指针指向空。

与数组按照下标来随机寻找元素不同，对于链表的其中一个节点A，我
们只能根据节点A的next指针来找到该节点的下一个节点B，再根据节点
B的next指针找到下一个节点C……

这正如地下党的联络方式，一级一级，单线传递。

那么，通过链表的一个节点，如
何能快速找到它的前一个节点呢？

要想让每个节点都能回溯到它的前置
节点，我们可以使用双向链表 。

什么是双向链表？
双向链表比单向链表稍微复杂一些，它的每一个节点除了拥有data和
next指针，还拥有指向前置节点的prev 指针。

接下来我们看一看链表的存储方式。
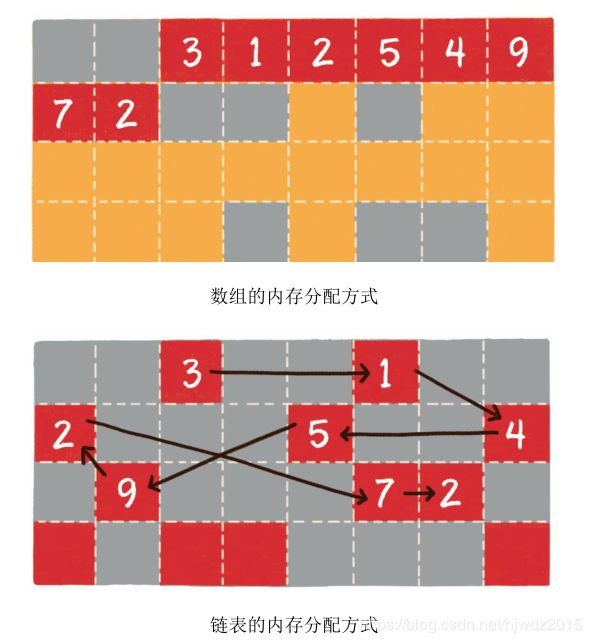
如果说数组在内存中的存储方式是顺序存储，那么链表在内存中的存储
方式则是随机存储 。
什么叫随机存储呢？

上一节我们讲解了数组的内存分配方式，数组在内存中占用了连续完整
的存储空间。而链表则采用了见缝插针的方式，链表的每一个节点分布
在内存的不同位置，依靠next指针关联起来。这样可以灵活有效地利用
零散的碎片空间。

图中的箭头代表链表节点的next指针

 

 

待继续。。。。。。。。。