题目连接
POJ1430
题目概述
判断第二类\(stirling\)数\(S(n,m)\)的奇偶性.数据规模\(n\)很大,\((1 \leq n \leq 10^9)\).
不算方法的做法
因为\(S(n,m)=m*S(n-1,m)+S(n-1,m-1)\),当\(m\)为偶数的时候,\(S(n,m)\)的奇偶性与\(S(n-1,m-1)\)一样;当\(m\)为奇数的时候,\(S(n,m)\)的奇偶性和\(S(n-1,m)+S(n-1,m-1)\)一样(为奇数的话,\(m\)可以替换为1,不改变奇偶性.然后得到一个式子:
\[S^*(n,m)= \begin{cases} S^*(n-1,m-1), \quad if\, m\%2 = 0\\ S^*(n-1,m)+S^*(n-1,m-1),\quad if\, m\%2 =1 \end{cases} \]
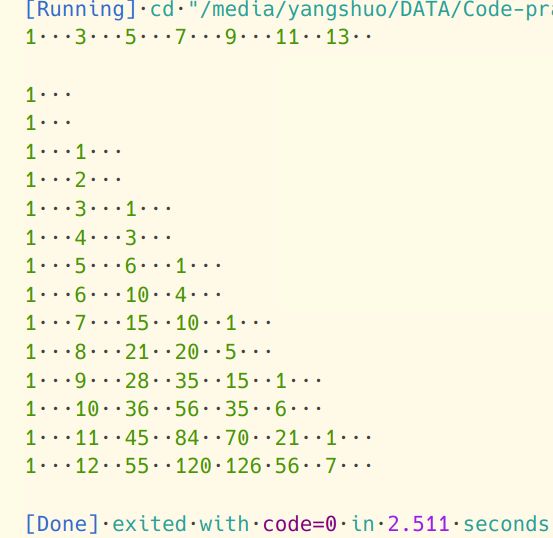
这样得到的\(S^*(n,m)\)与\(S(n,m)\)的奇偶性是一样的.对于\(S^*(n,m)\)当\(m\)为奇数时和组合数的递推式一样,因为\(S^*(n-1,m-1)=S*(n-2,m-2),((m-1)\%2=0)\),所以\(S^*(n,m)\)的结果与\(m\)列和\(m-2\)列有关,如果把奇数列单独拎出来的话,和组合数那个系数表很像:
第一列是\(C_{n'}^0\),第二列是\(C_{n'}^1\),\(\cdots\).第\(m\)列对应的应该是\(C_{n'}^{m/2}\).行的关系算出来是\(n'=n-1-m/2\).这\(m\)是奇数时的情况,用同样的方法可以推出偶数时的关系,最后可以同一成这个:
\[S^*(n,m)=C_{n-1-m/2}^{\frac{m+1}{2}-1} \]
对于组合数\(C_n^m\)奇偶性的判断有这样一个快速的方法,如果\(n\&m=m\),那么是奇数,否则是偶数.
代码实现
#include
using namespace std;
const int N = 100;
void solve(int n, int m) {
if( m > n){
cout<< "0"<