海量数据处理(位图和布隆过滤器)
哈希切割
给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址? 与上题条件相同,如何找到top K的IP?如何直接用Linux系统命令实现
解决思路
找到出现次数最多的IP地址
要找到前TopK的IP地址,就是要统计每个IP地址出现多少次
分割大文件:如果能将相同IP地址放到同一个文件中
哈希分割: 从源文件中获取一个IP地址---->IP%文件份数
- 每拿到一个IP地址后,用函数把IP地址转化为整型数据,再%上文件分数,就知道把IP地址放到哪个文件中去
- 这样,就可以统计每个IP地址出现多少次
//构建键值对
<IP地址的整型数据,次数>
- 统计哪个IP地址出现的次数比较多,用unordered_map,m[ip]++;每拿到一个IP地址的++。每个IP地址出现的次数,已经在unordered_map中保存起来
- 按类似的方法,统计每个文件中的IP地址的次数,最后用一个for()---->找出出现最多的IP地址
top K的IP
堆---->最多前K个IP地址—><次数,IP地址>
位图
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中。
- 遍历,时间复杂度O(N)
- 排序(O(NlogN)),利用二分查找: logN
位图解决
数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使用一个二进制比
特位来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0代表不存在。比如:
40亿的整型数据大概是16G的数据
用位图来映射的话 大概就是232-23=512M

解决
位图的实现
#pragma once
#include位图的应用
- 快速查找某个数据是否在一个集合中
- 排序 (数据不能有重复)
- 求两个集合的交集、并集等
- 操作系统中磁盘块标记
位图的题
- 给定100亿个整数,设计算法找到只出现一次的整数?
用两个比特位表示一个数据,8/2=4;那么位图中一个字节只能表示4个数据,232/22=1G。
取一个数据:哪个字节 哪两个比特位
if(00) //出现过0次
01
else if(01) //出现过多次
10
- 位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数
布隆过滤器
位图+哈希函数
特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。多个比特位代表数据的状态信息
布隆过滤器插入
如果向布隆过滤器中插入baidu,我们用三个哈希函数将三个位置置为1
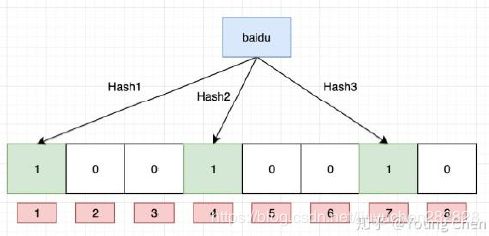
“baidu”---->1 4 7
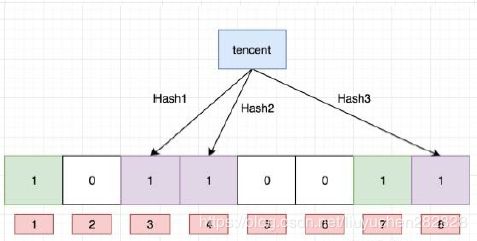
“tecent”---->3 4 8
hash1,hash2,hash3----->三个位置
检测三个位置的状态
如果三个位置只要有一个为0,说明数据一定不存在
布隆过滤器的查找
布隆过滤器的思想是将一个元素用多个哈希函数映射到一个位图中,因此被映射到的位置的比特位一定为1。所以可以按照以下方式进行查找:分别计算每个哈希值对应的比特位置存储的是否为零,只要有一个为零,代表该元素一定不在哈希表中,否则可能在哈希表中
布隆过滤器如果告诉你数据不存在,那么一定不存在,如果告诉你存在,则有可能存在。
布隆过滤器的插入和查找的实现
#pragma once
#include"biteset.hpp"
#include布隆过滤器的删除
布隆过滤器不能直接支持删除工作,因为在删除一个元素时,可能会影响其他元素
一种支持删除的方法:将布隆过滤器中的每个比特位扩展成一个小的计数器(整型数组),插入元素时给k个计数器(k个哈希函数计算出的哈希地址)加一,删除元素时,给k个计数器减一,通过多占用几倍存储空间的代价来增加删除操作。
缺陷:
- 无法确认元素是否真正在布隆过滤器中
- 存在计数回绕
布隆过滤器优点
- 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关
- 哈希函数相互之间没有关系,方便硬件并行运算
- 布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
- 在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
- 数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
- 使用同一组散列函数的布隆过滤器可以进行交、并、差运算
布隆过滤器缺陷
- 有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白名单,存储可能会误判的数据)
- 不能获取元素本身
- 一般情况下不能从布隆过滤器中删除元素
- 如果采用计数方式删除,可能会存在计数回绕问题
布隆过滤器
- 给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法
答:给一个布隆过滤器,将一个文件的数据映射里面去。如果整体映射不完,先映射一部分。从另外一个文件拿一个数据在布隆过滤器里面找,如果有,数据存在就算是两个文件的交集。
倒排索引
给上千个文件,每个文件大小为1K—100M。给n个词,设计算法对每个词找到所有包含它的文件,你只有100K内存
