DFS遍历以及反转二叉树Python实现
如果一个二叉树,我们要按照深度优先方式遍历它,需要做三件事情:遍历左子树、遍历右子树和访问根节点。下面使用L、R、D表示这三项工作。
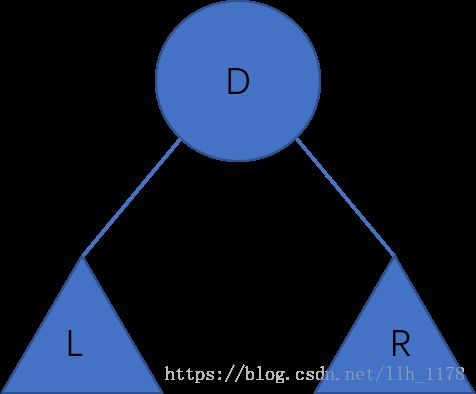
选择这三项工作的不同顺序,就可以得到三种常见遍历顺序:
1. 先根序遍历(按照DLR顺序)
2. 中根序遍历(按照LDR顺序)
3. 后根序遍历(按照LRD顺序)
二叉树的list实现
二叉树是递归结构,Python的list也是递归结构。基于list类型很容易实现二叉树,例如,可以如下设计:
1. 空树用None表示
2. 非空二叉树用包含三个元素的表[d, l, r]表示,其中d 表示存在根节点的元素,l和r是两棵子树,采用与整个二叉树同样结构的list表示。
例如:

[‘A’, [‘B’, None, None],
[‘C’, [‘D’, [‘F’, None, None], [‘G’, None, None]],
[‘E’, [‘H’, None, None], [‘I’, None, None]]]]
下面就用Python代码实现:
class BinTreeList(object):
def BinTree(self, data, left=None, right=None):
return [data, left, right]
def root(self, btree):
return btree[0]
def left(self, btree):
return btree[1]
def right(self, btree):
return btree[2]
def set_root(self, btree, data): # 设置root结点
btree[0] = data
def set_left(self, btree, left): # 设置左子树
btree[1] = left
def set_right(self, btree, right): # 设置右子树
btree[2] = right
def preorder(self, btree): # 先根序遍历
if btree is not None:
print(self.root(btree))
self.preorder(self.left(btree))
self.preorder(self.right(btree))
def midorder(self, btree): # 中根序遍历
if btree is not None:
self.midorder(self.left(btree))
print(self.root(btree))
self.midorder(self.right(btree))
def posorder(self, btree): # 后根序遍历
if btree is not None:
self.posorder(self.left(btree))
self.posorder(self.right(btree))
print(self.root(btree))
def reverse(self, btree): # 反转二叉树
if btree is not None:
btree[1], btree[2] = btree[2], btree[1]
self.reverse(self.left(btree))
self.reverse(self.right(btree))
下面,我们进行测试:
if __name__ == "__main__":
bintree = BinTreeList()
t1 = bintree.BinTree("A", bintree.BinTree("B"),
bintree.BinTree("C",
bintree.BinTree("D", bintree.BinTree("F"), bintree.BinTree("G")),
bintree.BinTree("E", bintree.BinTree("H"), bintree.BinTree("I"))))
print(t1)
bintree.preorder(t1)
bintree.midorder(t1)
bintree.posorder(t1)
print(bintree.root(t1))
[‘A’, [‘B’, None, None], [‘C’, [‘D’, [‘F’, None, None], [‘G’, None, None]], [‘E’, [‘H’, None, None], [‘I’, None, None]]]]
然后,可以分别测试先、中、后根序遍历是否准确。
最后,我们可以反转二叉树,看看反转之后的二叉树是什么样的。
if __name__ == "__main__":
bintree = BinTreeList()
t1 = bintree.BinTree("A", bintree.BinTree("B"),
bintree.BinTree("C",
bintree.BinTree("D", bintree.BinTree("F"), bintree.BinTree("G")),
bintree.BinTree("E", bintree.BinTree("H"), bintree.BinTree("I"))))
# bintree.set_left(bintree.left(t1), bintree.BinTree(5))
print(t1)
bintree.reverse(t1)
bintree.preorder(t1)
[A,C,E,I,H,D,G,F,B]——这就是反转之后的二叉树先根遍历结果,其实就是将左右子树的结点相互调换。