【入门算法】寻路系统：BFS&DFS

最后更新于2019.3.3
应一些朋友的请求，我就准备起笔写这篇博客了，因为本人非常懒，就不画一大堆图片来解释说明了，尽量只靠文字解决。最后补上一句几乎固定的话：如果喜欢本文，记得点赞哦；如果对我的博客较为满意的话，可以点一下左边的关注哦

还是和以前的习惯一样，先上OJ题

逃离迷宫

?戳这里可以前往原题

题目描述

王子深爱着公主。但是一天，公主被妖怪抓走了，并且被关到了迷宫。经过了常人难以想像的努力，王子到了这个迷宫，但是迷宫太过复杂，王子想知道到底有没有路能通到公主的所在地，机智的你一定能帮助他解决这个问题

输入

有多个测试数据。
每个测试数据的第一行是2个整数n,m （0 接着是个n*m的迷宫抽象图。其中，’#‘代表着墙壁,’.'代表着空地，'W’代表着王子的所在地。‘G’代表这公主的所在地，
王子只可以在空地上走，并且只能上，下，左，右的走。

输出

如果王子能到达公主的所在地，输出"Good life"
否则输出"Mission Failed"

样例输入

5 5
#####
#W. .#
###.#
#. .G#
#####

样例输出

Good life

有人问我为什么选择这样一道迷宫题，这道题没有需要输出时间，也没有其他限制要求，简直是一道干净的像一张白纸一样的迷宫题。而在这道题上，我们就可以来尝试两种做法（BFS&DFS）而不至于被大佬说BFS/DFS不适合这道题

然后这里再让我来吐槽一句：我不想用C语言写。
好吧，既然是帮朋友写，只好用C语言写了，主要的解释部分也用C语言写了。但是最后会补上C++的代码，如果是C语言的小白，可以只看前面的代码哦。

最后在解释前补上一句：我的BFS和DFS也是自学的，代码充斥的是我自己想法和写法，貌似同一些大佬写的代码差距有点大（但是原理相同），希望各位读者能够习惯

无论哪种方法都需要考虑到的东西

这里来先讨论一下无论哪种方法都需要的东西，这里给出问题列表：

1. 关于地图的保存
2. 关于路径的一个最重要的定律

对于这两个问题，我们给出以下解决方案：

1. 用int的二维数组来保存地图，用0表示空地，1表示墙体，2表示终点（起点其实没有必要保存）。
2. 对地图进行更新，每个到达过的地点，都把地图改成1，1是墙，也可以理解为不允许到达已经到达过的点。

BFS（Breadth First Search）广度优先查找

我想让读者先联想一个场景：一个湖泊里，在湖泊中间丢入一个石块，会形成波浪向四周涌去（这里我们先设定：波浪碰到障碍物不会反弹，而是直接消失，先不说为什么这么设定）。当波浪向四周涌去时碰到了石块等等的时候，这一处的波浪会消失，但是其他波浪并不会受到影响，并且，石块背后的位置，会由石块侧边的波浪覆盖掉。而我们假设湖泊边缘上有一个小洞，当有一处的波浪到达小洞时，我们也即找到了路径，即此处波浪走过的路径。

现在，我们把波浪类比做一个人，把湖泊的每一秒情况拍下来，做成一张张间隔为一秒的图片组。
根据以上的真实情况，我们定下了以下几条规则：

1. 人每一秒都会向所有方向前进（我们这里假设这个人分裂了……），但不会走回头路。
2. 如果一个人遇到了石头，这个人就放弃所有行动
3. 当有一个人到达终点时，所有人的行动都结束了，并且，这个人一定是最先到达终点的（这一点可以通过图片组来理解）

那么，我们可以这样写：我们写一个自定义函数，输入一个地点，然后做在这个函数体内，四次调用该函数，这四次分别是这个输入地点的四个方向 。来一次疯狂的递归。
那么我们可以写出伪代码：

int BFS(int x,int y)
{
	if(x,y)是终点return 1;
	if(x,y)是一个可以访问的点（可访问即这个点对应的不是墙也没有到达过）
	{
		设置(x,y)为不可访问的点;
		return BFS(x-1,y)||BFS(x+1,y)||BFS(x,y-1)||BFS(x,y+1);//调用四个方向的点，因为我们只要输出是否能到达即可（这里只是为了方便理解而这样写，因为这个是伪代码，不需要遵循程序的顺序，实际上这行代码是按照DFS的规则执行的，所以要真的把这个写成c语言代码，不太可能哦）
	}
	else
	{
		return 0;
	}
}

当然如果你强大到可以把伪代码改写成c语言代码，对于一些地图较小的，还是可以通过的。但是对于那些地图较大的，如果你想闻烤熟的CPU的味道的话，可以尝试一下这个方法。
当然这个烤熟的CPU只是说说的，一般情况下都是内存先炸掉
那我们只好换一种递归方法了，优化一下内存问题。我们知道波浪是呈圆形的，假若当前一秒的所有的人按照某一个顺序（顺/逆时针）进入下一秒，也即向所有方向派出他的分裂人，我们可以知道这样一个显而易见的定律：最新生成的分裂人一定是最后进行判断的（这个即是BFS的精华所在，参考下面的BFS示意图，好好理解后，再往下看）

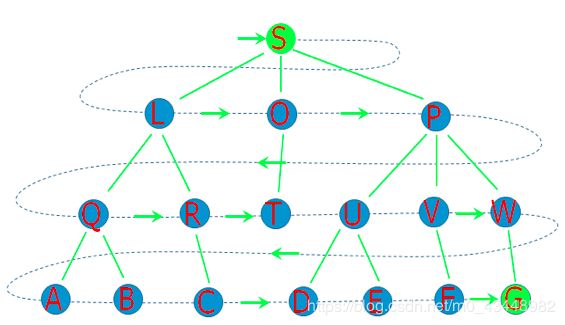
这里我们引出一个定义：

队列

遵循先进先出的原则，即最先进入队列的元素最先离开队列
将新的分裂人放在队列末尾，然后取出队列开头的人进入下一步

那么我们可以定义这样一个数组，每次分裂之后，把每一个分裂的人存入这个数组中。我们需要两个int类型的变量，一个指向队列的头，一个指向队列的尾（因为队列本身是需要删除掉队列头的，但是如果你删掉的话还需要把剩下的都前移一个单位，这样太浪费时间了，不如写一个指向头的整型变量）

这样我们就可以写出我们想要的AC代码了

//BFS查找
#include 
 
int roadmap[55][55],dir[4][2]={0,1,0,-1,1,0,-1,0};
//roadmap是地图（本来是用C++写的，为了避免被占用所以如此命名）dir变量在后面有妙用，可以学习一下？
int n,m;
 
struct node
{
    int x;
    int y;
};//一个点的结构
 
struct node stdcqueue[1000];//这里这个变量即我口中的队列
int startl,endr;
 
void BFS()//BFS递归
{
    if (startl==endr)//如果起点等于终点，也即是队列内无元素
    {
        printf("Mission Failed\n");
        return;
    }
    struct node curnode=stdcqueue[startl];//保存队列的头
    startl++;//“删掉”队列头
    struct node nextnode;
    for (int i=0; i<4; i++)//四个方向移动
    {
        nextnode=curnode;
        nextnode.x+=dir[i][0];
        nextnode.y+=dir[i][1];
        if (nextnode.x>=0 && nextnode.x<n && nextnode.y>=0 && nextnode.y<m)//判断点是否合法
        {
            if (roadmap[nextnode.x][nextnode.y]==0)
            {
                roadmap[nextnode.x][nextnode.y]=1;//把到达过的点设为墙，无法再次通过
                stdcqueue[endr]=nextnode;
                endr++;
            }
            else if (roadmap[nextnode.x][nextnode.y]==2)//到达终点判断
            {
                printf("Good life\n");
                return;
            }
        }
    }
    BFS();
    return;
}
 
int main()
{
    while (scanf("%d%d",&n,&m)!=EOF)
    {
    	getchar();//读取掉回车
        startl=0;
        endr=1;
        for (int i=0; i<n; i++)
        {
            for (int j=0; j<m; j++)
            {
                char c;
                c=getchar();
                switch (c)
                {
                    case '#':
                        roadmap[i][j]=1;
                        break;
                    case '.':
                        roadmap[i][j]=0;
                        break;
                    case 'W':
                        stdcqueue[0].x=i;//起点
                        stdcqueue[0].y=j;//起点
                        roadmap[i][j]=1;
                        break;
                    case 'G':
                        roadmap[i][j]=2;
                        break;
                    default:
                        break;
                }
            }
            getchar();//读取掉回车
        }
        BFS();
    }
    return 0;
}

希望各位读者能够通过本文能理解清楚BFS查找
下面将介绍DFS查找

DFS（Depth First Search）深度优先搜索

这里我们再来做一次联想
我相信各位读者一定玩过走迷宫类型的游戏，但是是否知道走迷宫的口诀，即对于一个可以走通的迷宫，则这个规则一定能找到答案。这个规则有以下两条

1. 碰壁往回走
2. 遇到岔路口，靠着右壁走

这两天规则其实可以合并为一条：将你的右手始终放在墙壁上
好吧，我承认规则有点难理解，但是其实这就是DFS搜索的一种解释：如果遇到死路就回溯到上一步，并回归到上一步时的状态，选择一个新的方向走下去
这里面最重要的一句话：回溯到上一步的状态

这里我不再对这句话进行过多的解释，过多的解释容易让读者更加迷茫，这里就直接贴出代码了

这里的DFS代码我直接贴出了最简洁，同样也最难懂，的版本，各位小白可能一下子会看不出来，我也不过多的解释了，如果看不懂，可以尝试自己写，参照上面的BFS代码。
怎么参照呢？
BFS用的是队列，遵循先进先出，而DFS遵循的是后进先出，这个是堆栈的规则。也即可以将上面的BFS代码从取出队列头改成取出队列尾，并对一些状态的变化进行调整，即可写出（由于与BFS代码重叠部分很多，所以我也就不再写了）

//DFS搜索
#include

int n,m;
int roadmap[55][55],dir[4][2]={0,1,0,-1,1,0,-1,0};
int startx,starty;

int DFS(int x,int y)
{
    
    int i;
    //这里是整个DFS的精髓所在
    for (i=0; i<4; i++)
    {
        //向一个方向前进
        x+=dir[i][0];
        y+=dir[i][1];
        //下面三个if语句用来判断下一步是否合法，即下一个点是否可以访问
        if (x<0 || x>=n || y<0 || y>=m)
        {
            continue;
        }
        if (roadmap[x][y]==1)
        {
            continue;
        }
        if (roadmap[x][y]==2)//到达终点
        {
            return 1;
        }
        roadmap[x][y]=1;
        //DFS查找
        if(DFS(x, y))
        {
            return 1;
        }
        //状态回到这一步没有走到状态
        x-=dir[i][0];
        y-=dir[i][1];
        roadmap[x][y]=0;
    }
    return 0;
}

int main()
{    
    while (scanf("%d%d",&n,&m)!=EOF)
    {
        getchar();//读取掉回车
        for (int i=0; i<n; i++)
        {
            for (int j=0; j<m; j++)
            {
                char c;
                c=getchar();
                switch (c)
                {
                    case '#':
                        roadmap[i][j]=1;
                        break;
                    case '.':
                        roadmap[i][j]=0;
                        break;
                    case 'W':
                        startx=i;
                        starty=j;
                        roadmap[i][j]=1;
                        break;
                    case 'G':
                        roadmap[i][j]=2;
                        break;
                    default:
                        break;
                }
            }
            getchar();//读取掉回车
        }
        if(DFS(startx, starty))
        {
            printf("Good life\n");
        }
        else
        {
            printf("Mission Failed\n");
        }
    }
    return 0;
}

BFS和DFS优劣分析

BFS用内存换时间，相对DFS而言速度快，只要有“一个人”到达终点即完成，容易得到最短时间。但是代价则是需要很大的内存去保存队列
DFS用时间换内存，相对BFS而言内存占用小，但是如果需要求出到达目的地的最短时间时，还需要进行处理：剪枝即是如此还需要把所有情况遍历完才能得出答案。

给出C++的进阶BFS代码

（DFS的进阶代码话就是上面贴的那个）
这里就不再过多的解释说明C++的BFS代码了

//由于markdown编辑器不能支持C++语法的高亮模式，看起代码来稍微有点难受啊
#include 
 
using namespace std;
 
int roadmap[55][55],dir[4][2]={0,1,0,-1,1,0,-1,0};
int n,m,startn,startm;
 
typedef pair<int, int> node;
 
queue<node> q;
 
void BFS()
{
    if (q.empty())
    {
        cout<<"Mission Failed"<<endl;
        return;
    }
    node curnode=q.front();
    q.pop();
    node nextnode;
    for (int i=0; i<4; i++)
    {
        nextnode=curnode;
        nextnode.first+=dir[i][0];
        nextnode.second+=dir[i][1];
        if (nextnode.first>=0 && nextnode.first<n && nextnode.second>=0 && nextnode.second<m)
        {
            if (roadmap[nextnode.first][nextnode.second]==0)
            {
                roadmap[nextnode.first][nextnode.second]=1;
                q.push(nextnode);
            }
            else if (roadmap[nextnode.first][nextnode.second]==2)
            {
                cout<<"Good life"<<endl;
                return;
            }
        }
    }
    BFS();
    return;
}
 
int main()
{
    ios::sync_with_stdio(false);
 
    while (cin>>n>>m)
    {
        while (!q.empty())
        {
            q.pop();
        }
        for (int i=0; i<n; i++)
        {
            for (int j=0; j<m; j++)
            {
                char c;
                cin>>c;
                switch (c)
                {
                    case '#':
                        roadmap[i][j]=1;
                        break;
                    case '.':
                        roadmap[i][j]=0;
                        break;
                    case 'W':
                        startn=i;
                        startm=j;
                        roadmap[i][j]=1;
                        break;
                    case 'G':
                        roadmap[i][j]=2;
                        break;
                    default:
                        break;
                }
            }
        }
        node newnode(startn,startm);
        q.push(newnode);
        BFS();
    }
    return 0;
}