Logistic Regression（逻辑回归）原理及公式推导

逻辑回归是广义线性模型

广义线性模型：

是指让模型的预测值去逼近y的衍生物，譬如说，假设我们认为示例所对应的输出标记是在指数尺度上的变化，那就可以将输出标记的对数作为线性模型逼近目标，即 lny=w2x+b l n y = w 2 x + b 更一般的考虑单调可微函数g()令 y=g−1(wTx+b) y = g − 1 ( w T x + b ) ，这样得到的模型称为广义线性模型。广义线性模型中，只需要找一个单调可微的函数将分类任务的真是标记y与线性回归模型的预测值联系起来。

我们知道，线性回归的公式如下： z=wTx+b z = w T x + b 考虑二分类任务，其输出标记y=1 or 0 ，于是我们需要将z转换为0/1 值，最理想的是‘单位阶跃函数’

即若z大于0 就判为正例，小于0就判为假例，预测值为临界值的时候可以任意判断。
但是阶跃函数不连续，因此放弃选用。
于是我们希望找到一个能在一定程度上提到近似单位阶跃函数的替代函数，并希望单调可微，因为sigmoid函数就出现了： hθ(x)=y=11+e−z h θ ( x ) = y = 1 1 + e − z ,其中 z=wTx+b z = w T x + b

我们可以看到，sigmoid的函数输出是介于（0，1）之间的，中间值是0.5，于是之前的公式 hθ(x) 的含义就很好理解了，因为 hθ(x) 输出是介于（0，1）之间，也就表明了数据属于某一类别的概率，例如 ：
z<0.5 则说明当前数据属于正类；
z>0.5 则说明当前数据属于反类。
所以我们可以将sigmoid函数看成样本数据的概率密度函数。
Logistic Regression算法是将线性函数的结果映射到了sigmoid函数中。
可以将上面的式子变换一下：

---

1y=1+e−(wTx+b) 1 y = 1 + e − ( w T x + b )

1−1y=e−(wTx+b) 1 − 1 y = e − ( w T x + b ) ,然后两边求对数

lny1−y=wTx+b l n y 1 − y = w T x + b

---

若将y视为样本x作为正例的可能性，则1-y就是作为反例的可能性，两者的比值称为‘几率’，再区对数，就是‘对数几率’。

极大似然估计，估计参数

有了上面的公式，我们接下来需要做的就是怎样去估计参数 θ 了。
首先我们来看， θ 函数的值有特殊的含义，它表示 hθ(x) h θ ( x ) 结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

---

p(y=1|x;θ)=hθ(x) p ( y = 1 | x ; θ ) = h θ ( x )
p(y=0|x;θ)=1−hθ(x) p ( y = 0 | x ; θ ) = 1 − h θ ( x )

---

根据上式，接下来我们可以使用概率论中极大似然估计的方法去求解损失函数，首先得到概率函数为：

---

P(y|x;θ)=(hθ(x))y∗(1−hθ(x))1−y P ( y | x ; θ ) = ( h θ ( x ) ) y ∗ ( 1 − h θ ( x ) ) 1 − y 上面两个式子的综合

又有样本之间是相互独立的，即得似然函数如下：

L(θ)=∏mi=1P(y(i)|x(i);θ) L ( θ ) = ∏ i = 1 m P ( y ( i ) | x ( i ) ; θ )

L(θ)=∏mi=1(hθ(x(i)))y(i)∗(1−hθ(x(i)))1−y(i) L ( θ ) = ∏ i = 1 m ( h θ ( x ( i ) ) ) y ( i ) ∗ ( 1 − h θ ( x ( i ) ) ) 1 − y ( i )

---

取对数似然函数：

l(θ)=log(L(θ))=∑mi=1log((hθ(x(i)))y(i))+log((1−hθ(x(i)))1−y(i)) l ( θ ) = l o g ( L ( θ ) ) = ∑ i = 1 m l o g ( ( h θ ( x ( i ) ) ) y ( i ) ) + l o g ( ( 1 − h θ ( x ( i ) ) ) 1 − y ( i ) )

l(θ)=log(L(θ))=∑mi=1y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i))) l ( θ ) = l o g ( L ( θ ) ) = ∑ i = 1 m y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) )

最大似然估计就是要求得使 l(θ) 取最大值时的 θ ，这里可以使用梯度上升法求解。我们稍微变换一下：

J(θ)=−1ml(θ) J ( θ ) = − 1 m l ( θ )

因为乘了一个负的系数 −1/m − 1 / m ，然后就可以使用梯度下降算法进行参数求解了.

---

最大似然估计就是要求得使 l(θ) 取最大值时的 θ ，这里可以使用梯度下降法求解.
为了方便理解，我们先对一个样本进行分析，首先，对参数求导：
用到了复合函数求导，要是不懂复合函数求导的要先去弄懂复合函数求导

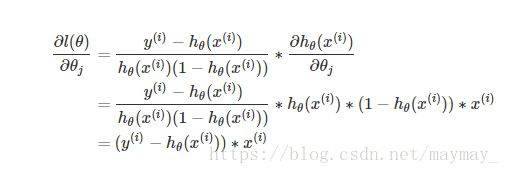
结合上面的 J(θ)=−1ml(θ) J ( θ ) = − 1 m l ( θ ) ,故用梯度下降的方法求 θ θ 的整体公式可以写成:

θj=θj−(−1m∑mi=1l(θ)) θ j = θ j − ( − 1 m ∑ i = 1 m l ( θ ) )

也就是

θj=θj+1m∑mi=1l(θ) θ j = θ j + 1 m ∑ i = 1 m l ( θ )

将上面求得的 l(θ) l ( θ ) 带进去式子里面得到

θj=θj+1m∑mi=1(y(i)−hθ(x(i)))∗x(i)   (for every j) θ j = θ j + 1 m ∑ i = 1 m ( y ( i ) − h θ ( x ( i ) ) ) ∗ x ( i )       ( f o r   e v e r y   j )

将括号式子的负号提出来，就得到了我们平时见到的式子

θj=θj−1m∑mi=1(hθ(x(i))−y(i))∗x(i)   (for every j) θ j = θ j − 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ∗ x ( i )       ( f o r   e v e r y   j )

其实这个式子跟线性回归的的是一样的，唯一不同的，就是逻辑回归里面 hθ(x(i)) h θ ( x ( i ) ) 是sigmoid函数。