JS递归算法经典案例与分析

什么是递归函数？

简单定义：当函数直接或者间接调用自己时，则发生了递归.” 说起来简单, 但是理解起来复杂, 因为递归并不直观, 也不符合我们的思维习惯, 相对于递归, 我们更加容易理解迭代. 因为我们日常生活中的思维方式就是一步接一步的, 并且能够理解一件事情做了N遍这个概念. 而我们日常生活中几乎不会有递归思维的出现.

举个简单的例子：
求1到5的累加和 下面是传统的方式, 我们一般都这样通过迭代来计算累加和, 也很好理解.

而事实上, 我们也可以通过递归来完成这样的任务.

只不过, 我们都不这么做罢了, 虽然这样的实现有的时候可能代码更短, 但是很明显, 从思维上来说更加难以理解一些. 当然, 我是说假如你不是习惯于函数式语言的话. 这个例子相对简单, 稍微看一下还是能明白吧.

作为这么简单的例子, 两种算法其实大同小异, 虽然我们习惯迭代, 但是, 也能看到, 递归的算法无论是从描述上还是实际实现上, 并不比迭代要麻烦.

理解递归

在初学递归的时候, 看到一个递归实现, 我们总是难免陷入不停的回溯验证之中, 因为回溯就像反过来思考迭代, 这是我们习惯的思维方式, 但是实际上递归不需要这样来验证.
要实现递归要书写两个内容:
一个是满足结束条件的时候结束函数
一个是不满足结束条件的时候要执行的代码

我们拿上面案例来作为分析：
1.我要书写一个函数叫做add
2.这个函数有形参n,调用的时候:add(n)
3.我这个add函数的功能是计算任意一个数1到n的累加和。
这里以n=5来分析

分析思路：

第一遍
计算输入的n即n=5;程序开始执行，
返回的是add（ 5 - 1） + 5 的值，即返回的是add(4)+5的值，add(4)的值是多少？
因为没有具体数值,程序就要去执行add(4)，即调用第二遍

第二遍
计算add(4)，程序开始执行，
返回的是add（ 4 - 1） + 4 的值，即返回的是add(3)+4的值，add(3)的值是多少？
因为没有具体数值,程序就要去执行add(3)，即调用第三遍

第三遍
计算add(3)，程序开始执行，
返回的是add（ 3 - 1） + 3 的值，即返回的是add(2)+3的值，add(2)的值是多少？
因为没有具体数值,程序就要去执行add(2)，即调用第四遍

第四遍
计算add(2)，程序开始执行，
返回的是add（ 2 - 1） + 3 的值，即返回的是add(1)+2的值，add(1)的值是多少？
因为没有具体数值,程序就要去执行add(1)，即调用第五遍

第五遍
计算add(1)，程序开始执行，
当n==1 时，满足第一个条件，返回的值是1,是一个具体数值，此时函数不在调用自身。
看到这里我们就应该明白此时

add（1）=1
add（2）=add（1）+2 =1+2
add（3）=add（2）+3=1+2+3
add（4）=add（3）+4=1+2+3+4
add（5）=add（4）+5=1+2+3+4+5
…
…
add（n)=add(n-1)+n=1+2+3+4+5+…+n

注意点：使用递归时，要有结束条件，否则就会“死循环”，造成浏览器崩溃。

使用递归

既然递归比迭代要难以理解, 为啥我们还需要递归呢? 从上面的例子来看, 自然意义不大, 但是很多东西的确用递归思维会更加简单……

经典的例子就是斐波那契数列（Fibonacci sequence），又称黄金分割数列、
因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，
指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，
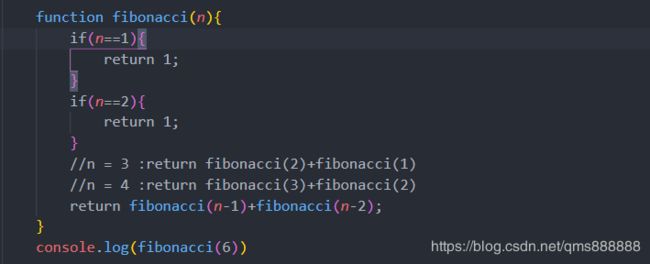
斐波那契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 3）

        有了递归的算法, 用程序实现实在再简单不过了:

改为用迭代实现呢? 你可以试试.

递归的问题

当然, 这个世界上没有啥时万能的, 递归也不例外, 首先递归并不一定适用所有情况, 很多情况用迭代远远比用递归好了解, 其次, 相对来说, 递归的效率往往要低于迭代的实现, 同时, 内存耗用也会更大, 虽然这个时候可以用尾递归来优化, 但是尾递归并不是一定能简单做到.它是依据数据结构的栈的原理，不断开辟新的内存空间以满足程序需要，而不是不断改变已有内存空间的值来满足程序需要，所以递归是一种极具消耗内存资源的算法思维，所以在现实项目中，除非代码量影响过大，否则能不用递归就不用递归.

参考

精通递归程序设计