动态规划类题目常规思路—Leetcode-thinking_record13
打家劫舍(Easy)
LeetCode 198.House Robber
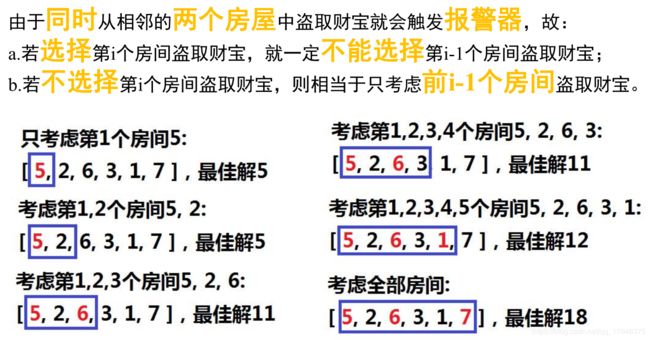
在一条直线上,有n个房屋,每个房屋中有数量不等的财宝,有一个盗贼希望从房屋中盗窃财宝,由于房屋中有报警器,如果同时从相邻的两个房屋中盗取财宝就会触发报警器。问在不触发报警器的前提下,最多可获取多少财宝?
总体思路
细节设计
代码实现
#include
#include
class Solution {
public:
int rob(std::vector& nums) {
if (nums.size() == 0){
return 0;
}
if (nums.size() == 1){
return nums[0];
}
std::vector dp(nums.size(), 0);
dp[0] = nums[0];
dp[1] = std::max(nums[0], nums[1]);
for (int i = 2; i < nums.size(); i++){
dp[i] = std::max(dp[i-1], dp[i-2] + nums[i]);
}
return dp[nums.size() - 1];
}
};
int main(){
Solution solve;
std::vector nums;
nums.push_back(5);
nums.push_back(2);
nums.push_back(6);
nums.push_back(3);
nums.push_back(1);
nums.push_back(7);
printf("%d\n", solve.rob(nums));
return 0;
} 最大子段和(Easy)
LeetCode 53.Maximum Subarray
给定一个数组,求这个数组的连续子数组中,最大的那一段的和。
总体思路
细节设计
代码实现
#include
#include
class Solution {
public:
int maxSubArray(std::vector& nums) {
std::vector dp(nums.size(), 0);
dp[0] = nums[0];
int max_res = dp[0];
for (int i = 1; i < nums.size(); i++){
dp[i] = std::max(dp[i-1] + nums[i], nums[i]);
if (max_res < dp[i]){
max_res = dp[i];
}
}
return max_res;
}
};
int main(){
Solution solve;
std::vector nums;
nums.push_back(-2);
nums.push_back(1);
nums.push_back(-3);
nums.push_back(4);
nums.push_back(-1);
nums.push_back(2);
nums.push_back(1);
nums.push_back(-5);
nums.push_back(4);
printf("%d\n", solve.maxSubArray(nums));
return 0;
} 找零钱
LeetCode 322.Coin Change
已知不同面值的钞票,求如何用最少数量的钞票组成某个金额,求可以使用的最少钞票数量。如果任意数量的已知面值钞票都无法组成该金额,则返回-1.
总体思路
细节设计
代码实现
#include
#include
class Solution {
public:
int coinChange(std::vector& coins, int amount) {
std::vector dp;
for (int i = 0; i <= amount; i++){
dp.push_back(-1);
}
dp[0] = 0;
for (int i = 1; i <= amount; i++){
for (int j = 0; j < coins.size(); j++){
if (i - coins[j] >= 0 && dp[i - coins[j]] != -1){
if (dp[i] == -1 || dp[i] > dp[i - coins[j]] + 1){
dp[i] = dp[i - coins[j]] + 1;
}
}
}
}
return dp[amount];
}
};
int main(){
Solution solve;
std::vector coins;
coins.push_back(1);
coins.push_back(2);
coins.push_back(5);
coins.push_back(7);
coins.push_back(10);
for (int i = 1; i<= 14; i++){
printf("dp[%d] = %d\n", i, solve.coinChange(coins, i));
}
return 0;
} 三角形
LeetCode 120.Triangle
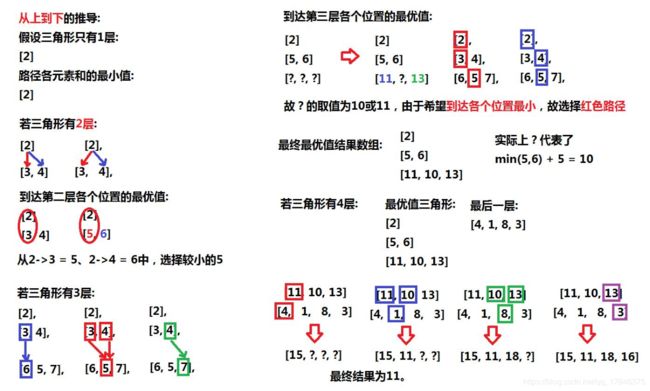
给定一个二维数组,其保持了一个数字三角形,求从数字三角形顶端到底端各数字和最小的路径之和,每次可以向下走相邻的两个位置。
总体思路
细节设计
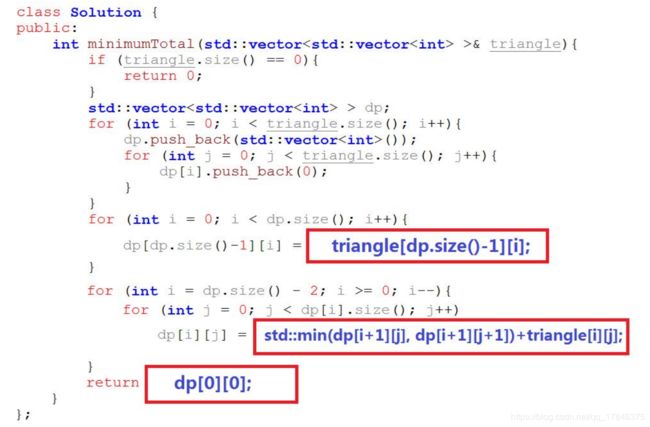
代码实现
#include
#include
class Solution {
public:
int minimumTotal(std::vector >& triangle){
if (triangle.size() == 0){
return 0;
}
std::vector > dp;
for (int i = 0; i < triangle.size(); i++){
dp.push_back(std::vector());
for (int j = 0; j < triangle.size(); j++){
dp[i].push_back(0);
}
}
for (int i = 0; i < dp.size(); i++){
dp[dp.size()-1][i] = triangle[dp.size()-1][i];
}
for (int i = dp.size() - 2; i >= 0; i--){
for (int j = 0; j < dp[i].size(); j++)
dp[i][j] = std::min(dp[i+1][j], dp[i+1][j+1])
+ triangle[i][j];
}
return dp[0][0];
}
};
int main(){
std::vector > triangle;
int test[][10] = {{2}, {3, 4}, {6, 5, 7}, {4, 1, 8, 3}};
for (int i = 0; i < 4; i++){
triangle.push_back(std::vector());
for (int j = 0; j < i + 1; j++){
triangle[i].push_back(test[i][j]);
}
}
Solution solve;
printf("%d\n", solve.minimumTotal(triangle));
return 0;
} 最长上升子序列
LeetCode 300.Longest Increasing Subsequence
已知一个未排序数组,求这个数组最长上升子序列的长度。
Solve1
总体思路
细节设计
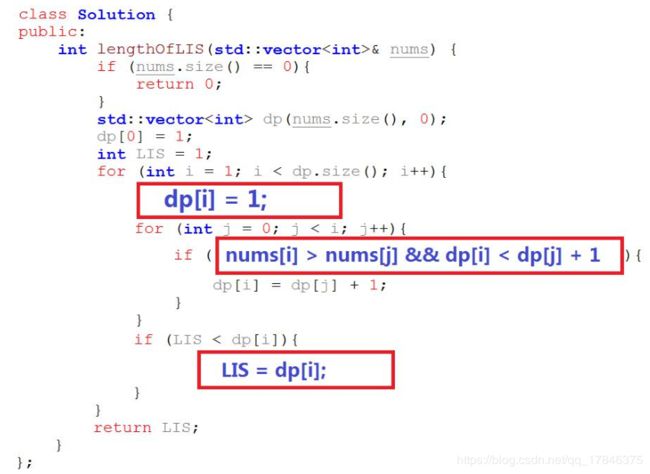
代码实现
#include
#include
class Solution {
public:
int lengthOfLIS(std::vector& nums) {
if (nums.size() == 0){
return 0;
}
std::vector dp(nums.size(), 0);
dp[0] = 1;
int LIS = 1;
for (int i = 1; i < dp.size(); i++){
dp[i] = 1;
for (int j = 0; j < i; j++){
if (nums[i] > nums[j] && dp[i] < dp[j] + 1){
dp[i] = dp[j] + 1;
}
}
if (LIS < dp[i]){
LIS = dp[i];
}
}
return LIS;
}
};
int main(){
int test[] = {10, 9, 2, 5, 3, 7, 101, 18};
std::vector nums;
for (int i = 0; i < 8; i++){
nums.push_back(test[i]);
}
Solution solve;
printf("%d\n", solve.lengthOfLIS(nums));
return 0;
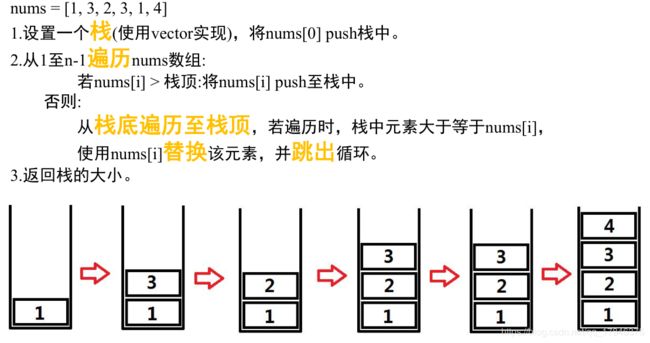
} Solve2
总体思路
细节设计
代码实现
LeetCode 300.Longest Increasing Subsequence(solve2)
#include
#include
class Solution {
public:
int lengthOfLIS(std::vector& nums) {
if (nums.size() == 0){
return 0;
}
std::vector stack;
stack.push_back(nums[0]);
for (int i = 1; i < nums.size(); i++){
if (nums[i] > stack.back()){
stack.push_back(nums[i]);
}
else{
for (int j = 0; j < stack.size(); j++){
if (stack[j] >= nums[i]){
stack[j] = nums[i];
break;
}
}
}
}
return stack.size();
}
};
int main(){
int test[] = {1, 3, 2, 3, 1, 4};
std::vector nums;
for (int i = 0; i < 6; i++){
nums.push_back(test[i]);
}
Solution solve;
printf("%d\n", solve.lengthOfLIS(nums));
return 0;
} LeetCode 300.Longest Increasing Subsequence(solve3)
#include
#include
int binary_search(std::vector nums, int target){
int index = -1;
int begin = 0;
int end = nums.size() - 1;
while (index == -1){
int mid = (begin + end) / 2;
if (target == nums[mid]){
index = mid;
}
else if (target < nums[mid]){
if (mid == 0 || target > nums[mid - 1]){
index = mid;
}
end = mid - 1;
}
else if (target > nums[mid]){
if (mid == nums.size() - 1 || target < nums[mid + 1]){
index = mid + 1;
}
begin = mid + 1;
}
}
return index;
}
class Solution {
public:
int lengthOfLIS(std::vector& nums) {
if (nums.size() == 0){
return 0;
}
std::vector stack;
stack.push_back(nums[0]);
for (int i = 1; i < nums.size(); i++){
if (nums[i] > stack.back()){
stack.push_back(nums[i]);
}
else{
int pos = binary_search(stack, nums[i]);
stack[pos] = nums[i];
}
}
return stack.size();
}
};
int main(){
int test[] = {1, 3, 2, 3, 1, 4};
std::vector nums;
for (int i = 0; i < 6; i++){
nums.push_back(test[i]);
}
Solution solve;
printf("%d\n", solve.lengthOfLIS(nums));
return 0;
} 最小路径和
LeetCode 64.Minimum Path Sum
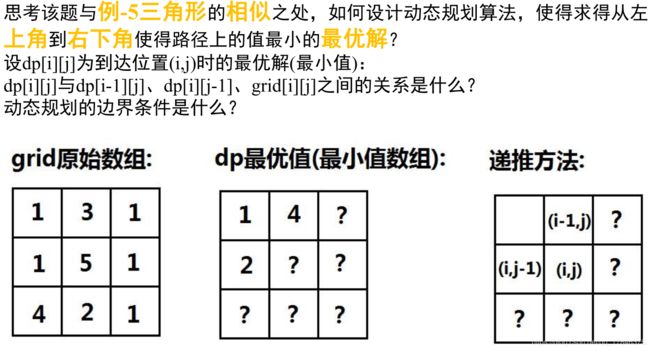
已知一个二维数组,其中存储了非负整数,找到从左上角到右下角的一条路径,使得路径上的和最小。(移动过程中只能向下或向右)
总体思路
细节设计
代码实现
#include
#include
class Solution {
public:
int minPathSum(std::vector >& grid) {
if (grid.size() == 0){
return 0;
}
int row = grid.size();
int column = grid[0].size();
std::vector >
dp(row, std::vector(column, 0));
dp[0][0] = grid[0][0];
for (int i = 1; i < column; i++){
dp[0][i] = dp[0][i-1] + grid[0][i];
}
for (int i = 1; i < row; i++){
dp[i][0] = dp[i-1][0] + grid[i][0];
for (int j = 1; j < column; j++){
dp[i][j] = std::min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
}
}
return dp[row-1][column-1];
}
};
int main(){
int test[][3] = {{1,3,1}, {1,5,1}, {4,2,1}};
std::vector > grid;
for (int i = 0; i < 3; i++){
grid.push_back(std::vector());
for (int j = 0; j < 3; j++){
grid[i].push_back(test[i][j]);
}
}
Solution solve;
printf("%d\n", solve.minPathSum(grid));
return 0;
} 地牢游戏
LeetCode 174.Dungeon Game
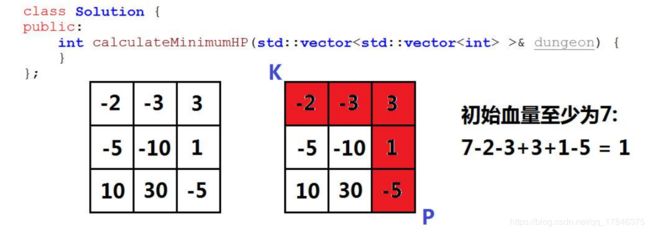
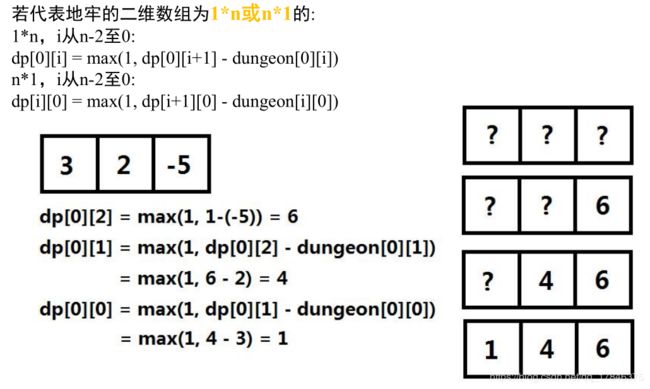
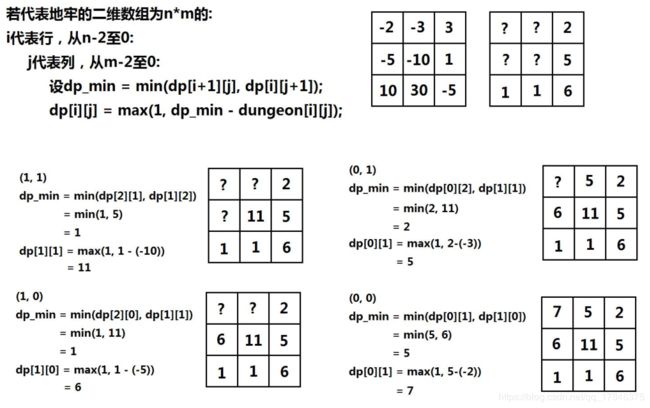
已知一个二维数组,左上角代表骑士的位置,右下角代表公主的位置,二维数组中存储整数,正数可以给骑士增加生命值,负数会减少骑士的生命值,问骑士初始时至少是多少生命值,才可保证骑士在行走的过程中至少保持生命值为1。(骑士只能向下或向右行走)
总体思路
细节设计
代码实现
#include
#include
class Solution {
public:
int calculateMinimumHP(std::vector >& dungeon) {
if (dungeon.size() == 0){
return 0;
}
std::vector >
dp(dungeon.size(), std::vector(dungeon[0].size(), 0));
int row = dungeon.size();
int column = dungeon[0].size();
dp[row-1][column-1] = std::max(1, 1-dungeon[row-1][column-1]);
for (int i = column-2; i>=0; i--){
dp[row-1][i] = std::max(1,
dp[row-1][i+1] - dungeon[row-1][i]);
}
for (int i = row-2; i>=0; i--){
dp[i][column-1] = std::max(1,
dp[i+1][column-1] - dungeon[i][column-1]);
}
for (int i = row-2; i>=0; i--){
for (int j = column-2; j>=0; j--){
int dp_min = std::min(dp[i+1][j], dp[i][j+1]);
dp[i][j] = std::max(1, dp_min - dungeon[i][j]);
}
}
return dp[0][0];
}
};
int main(){
int test[][3] = {{-2, -3, 3}, {-5, -10, 1}, {10, 30, -5}};
std::vector > dungeon;
for (int i = 0; i < 3; i++){
dungeon.push_back(std::vector());
for (int j = 0; j < 3; j++){
dungeon[i].push_back(test[i][j]);
}
}
Solution solve;
printf("%d\n", solve.calculateMinimumHP(dungeon));
return 0;
}