2019.6.26 python实现机器学习----scikit-learn库
1.scikit-learn库的产生
scikit-learn最初是David Cournapeau在2007年Google夏令营的代码项目中首次实现的。后来Matthieu Brucher加入了这个项目,并开始将其作为论文工作的一部分。2010年,INRIA参与其中,并于2010年1月第一次公开发布scikit-learn的v0.1 beta版本。
该项目目前有30多名活跃的贡献者,并已获得INRIA,Google,Tinyclues和Python软件基金会的赞助。
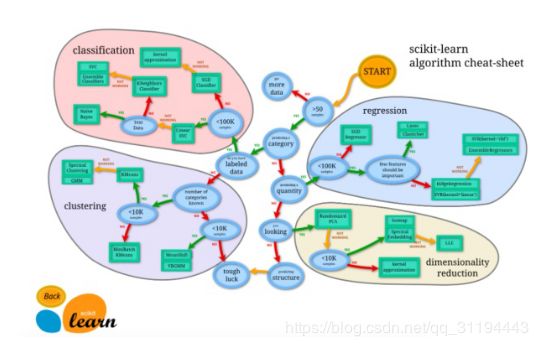
2.什么是scikit-learn
scikit-learn库是通过Python或c实现一系列有监督和无监督的学习算法,并提供封装好的Python借口供其他开发者使用。它是BSD许可证授权,并在许多Linux发行版下分发,鼓励学术和商业用途。
该库是基于SciPy(Scientific Python)构建的,必须先安装它才能使用scikit-learn。下面是scikit-learn依赖的一些Python包:
NumPy:操作N维数组的工具
SciPy:科学计算的基础库
Matplotlib:2D / 3D绘图
IPython:增强的交互式控制台
Sympy:数学对象符号化的计算方式
pandas:数据分析的基础库
scikit-learn库是基于SciPy库的扩展,增加了很多通用算法模块。由于该库提供很多机器学习算法,所以命名为scikit-learn。
该库的初衷是希望能够将机器学习快速运用于生成环境中,并保持健壮性和稳定性。这意味着该函数库必须具备易用、方便协作、文档详细和性能优越等特性。
虽然scikit-learn接口是Python,但是具体实现上用到了c语言,以提升性能,例如数组和矩阵运算的numpy,LAPACK,LibSVM以及cython等,都是用c语言实现的。
3.scikit-learn库的特点
该库专注于数据建模,但它不专注于加载、操作数据。如果你要处理数据,可以使用NumPy和Pandas。
scikit-learn提供了很多基础模型,包括:
聚类:用于对未标记的数据(如KMeans)进行分组。
交叉验证:用于估计监督模型对未知数据的性能。
数据集:常见的开源数据集。
降维:用于减少数据中的属性数量,以进行简化、可视化和特征选择,例如主成分分析。
集合方法:用于组合多个监督模型的预测结果。
特征提取:用于抽取图像和文本数据的属性。
特征选择:用于选择权重较大的属性。
参数调整:用于调整模型参数。
流形学习:用于总结和描述复杂的多维数据。
监督模型:包括线性模型,判别分析,朴素贝叶斯,惰性方法,神经网络,支持向量机和决策树等常见模型。
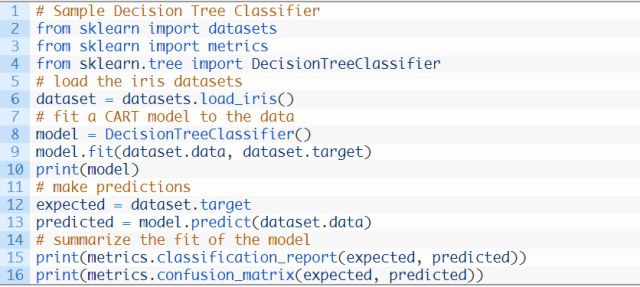
示例:分类和回归树
这里通过举例演示使用该库训练模型是多么简单。
在此示例中,我们使用决策树(CART)算法来模拟内置的Iris数据集。代码如下,使用加载数据,并通过决策树分类模型拟合数据,然后对训练数据进行预测。最后,打印分类准确度和混淆矩阵。
除去注释的代码,大概只用了10行代码就实现了这样一个分类模型!
4.资源
如果你想要学习scikit-learn,可以从它的官网页面中的快速入门教程开始,然后浏览用户指南和示例库,并深入学习你感兴趣的算法。
scikit-learn是一个比较完善的库,它的文档可以帮助你解决很多问题。可以重点关注文档的以下几个部分:
快速入门教程用户指南API参考示例库另外,如果你想通过书籍学习,下面两本书介绍了scikit-learn来训练机器学习模型。
学习scikit-learn:Python中的机器学习 (2013)使用Python构建机器学习系统 (2013)
5.安装pyCharm
6.安装库
7.代码实现
import numpy as np
from matplotlib import pylab as pl
# 定义训练数据
# (x,y)
x = np.array([1,3,2,1,3,])
y = np.array([14,24,18,17,27,])
# 回归方程求取函数
def fit(x,y):
# 确保x y数组长度小相等
if len(x) != len(y):
return
numerator = 0.0
denominator = 0.0
# mean:求均值
x_mean = np.mean(x)
y_mean = np.mean(y)
# 迭代x数组,y数组
for i in range(len(x)):
#
numerator += (x[i]-x_mean)*(y[i]-y_mean)
# square 求平方
denominator += np.square((x[i]-x_mean))
print('numerator:', numerator, 'denominator:', denominator)
b0 = numerator/denominator
b1 = y_mean - b0*x_mean
return b0, b1
# 定义预测函数
def predit(x, b0, b1):
return b0*x + b1
# 求取回归方程
b0, b1 = fit(x,y)
print('Line is:y = %2.0fx + %2.0f'% (b0, b1))
# 预测用另一组数据
x_test = np.array([0.5,1.5,2.5,3,4])
y_test = np.zeros((1,len(x_test)))
for i in range(len(x_test)):
y_test[0][i] = predit(x_test[i],b0,b1)
# 绘制图像
xx = np.linspace(0, 5)
yy = b0*xx + b1
pl.plot(xx,yy,'k-')
pl.scatter(x,y,cmap=pl.cm.Paired)
pl.scatter(x_test,y_test[0],cmap=pl.cm.Paired)
pl.show()8.Numpy包常用函数
| 生成函数 | 作用 |
| np.array( x) np.array( x, dtype) |
将输入数据转化为一个ndarray 将输入数据转化为一个类型为type的ndarray |
| np.asarray( array ) | 将输入数据转化为一个新的(copy)ndarray |
| np.ones( N ) np.ones( N, dtype) np.ones_like( ndarray ) |
生成一个N长度的一维全一ndarray 生成一个N长度类型是dtype的一维全一ndarray 生成一个形状与参数相同的全一ndarray |
| np.zeros( N) np.zeros( N, dtype) np.zeros_like(ndarray) |
生成一个N长度的一维全零ndarray 生成一个N长度类型位dtype的一维全零ndarray 类似np.ones_like( ndarray ) |
| np.empty( N ) np.empty( N, dtype) np.empty(ndarray) |
生成一个N长度的未初始化一维ndarray 生成一个N长度类型是dtype的未初始化一维ndarray 类似np.ones_like( ndarray ) |
| np.eye( N ) np.identity( N ) |
创建一个N * N的单位矩阵(对角线为1,其余为0) |
| np.arange( num) np.arange( begin, end) np.arange( begin, end, step) |
生成一个从0到num-1步数为1的一维ndarray 生成一个从begin到end-1步数为1的一维ndarray 生成一个从begin到end-step的步数为step的一维ndarray |
| np.mershgrid(ndarray, ndarray,...) |
生成一个ndarray * ndarray * ...的多维ndarray |
| np.where(cond, ndarray1, ndarray2) |
根据条件cond,选取ndarray1或者ndarray2,返回一个新的ndarray |
| np.in1d(ndarray, [x,y,...]) |
检查ndarray中的元素是否等于[x,y,...]中的一个,返回bool数组 |
| 矩阵函数 | 说明 |
| np.diag( ndarray) np.diag( [x,y,...]) |
以一维数组的形式返回方阵的对角线(或非对角线)元素 将一维数组转化为方阵(非对角线元素为0) |
| np.dot(ndarray, ndarray) | 矩阵乘法 |
| np.trace( ndarray) | 计算对角线元素的和 |
| 排序函数 |
说明 |
| np.sort( ndarray) |
排序,返回副本 |
| np.unique(ndarray) |
返回ndarray中的元素,排除重复元素之后,并进行排序 |
| np.intersect1d( ndarray1, ndarray2) np.union1d( ndarray1, ndarray2) np.setdiff1d( ndarray1, ndarray2) np.setxor1d( ndarray1, ndarray2) |
返回二者的交集并排序。 返回二者的并集并排序。 返回二者的差。 返回二者的对称差 |
| 一元计算函数 | 说明 |
| np.abs(ndarray) np.fabs(ndarray) |
计算绝对值 计算绝对值(非复数) |
| np.mean(ndarray) |
求平均值 |
| np.sqrt(ndarray) |
计算x^0.5 |
| np.square(ndarray) |
计算x^2 |
| np.exp(ndarray) |
计算e^x |
| log、log10、log2、log1p |
计算自然对数、底为10的log、底为2的log、底为(1+x)的log |
| np.sign(ndarray) |
计算正负号:1(正)、0(0)、-1(负) |
| np.ceil(ndarray) np.floor(ndarray) np.rint(ndarray) |
计算大于等于改值的最小整数 计算小于等于该值的最大整数 四舍五入到最近的整数,保留dtype |
| np.modf(ndarray) |
将数组的小数和整数部分以两个独立的数组方式返回 |
| np.isnan(ndarray) |
返回一个判断是否是NaN的bool型数组 |
| np.isfinite(ndarray) np.isinf(ndarray) |
返回一个判断是否是有穷(非inf,非NaN)的bool型数组 返回一个判断是否是无穷的bool型数组 |
| cos、cosh、sin、sinh、tan、tanh |
普通型和双曲型三角函数 |
| arccos、arccosh、arcsin、arcsinh、arctan、arctanh |
反三角函数和双曲型反三角函数 |
| np.logical_not(ndarray) |
计算各元素not x的真值,相当于-ndarray |
| 多元计算函数 |
说明 |
| np.add(ndarray, ndarray) np.subtract(ndarray, ndarray) np.multiply(ndarray, ndarray) np.divide(ndarray, ndarray) np.floor_divide(ndarray, ndarray) np.power(ndarray, ndarray) np.mod(ndarray, ndarray) |
相加 相减 乘法 除法 圆整除法(丢弃余数) 次方 求模 |
| np.maximum(ndarray, ndarray) np.fmax(ndarray, ndarray) np.minimun(ndarray, ndarray) np.fmin(ndarray, ndarray) |
求最大值 求最大值(忽略NaN) 求最小值 求最小值(忽略NaN) |
| np.copysign(ndarray, ndarray) |
将参数2中的符号赋予参数1 |
| np.greater(ndarray, ndarray) np.greater_equal(ndarray, ndarray) np.less(ndarray, ndarray) np.less_equal(ndarray, ndarray) np.equal(ndarray, ndarray) np.not_equal(ndarray, ndarray) |
> >= < <= == != |
| logical_and(ndarray, ndarray) logical_or(ndarray, ndarray) logical_xor(ndarray, ndarray) |
& | ^ |
| np.dot( ndarray, ndarray) | 计算两个ndarray的矩阵内积 |
| np.ix_([x,y,m,n],...) | 生成一个索引器,用于Fancy indexing(花式索引) |
| 文件读写 | 说明 |
| np.save(string, ndarray) | 将ndarray保存到文件名为 [string].npy 的文件中(无压缩) |
| np.savez(string, ndarray1, ndarray2, ...) | 将所有的ndarray压缩保存到文件名为[string].npy的文件中 |
| np.savetxt(sring, ndarray, fmt, newline='\n') | 将ndarray写入文件,格式为fmt |
| np.load(string) | 读取文件名string的文件内容并转化为ndarray对象(或字典对象) |
| np.loadtxt(string, delimiter) | 读取文件名string的文件内容,以delimiter为分隔符转化为ndarray |
表2.1.A.2 np常用函数
B NumPy.ndarray函数和属性:
| ndarray.ndim | 获取ndarray的维数 |
| ndarray.shape | 获取ndarray各个维度的长度 |
| ndarray.dtype | 获取ndarray中元素的数据类型 |
| ndarray.T | 简单转置矩阵ndarray |
表2.1.B.1 ndarray属性
| 函数 | 说明 |
| ndarray.astype(dtype) | 转换类型,若转换失败则会出现TypeError |
| ndarray.copy() | 复制一份ndarray(新的内存空间) |
| ndarray.reshape((N,M,...)) | 将ndarray转化为N*M*...的多维ndarray(非copy) |
| ndarray.transpose((xIndex,yIndex,...)) | 根据维索引xIndex,yIndex...进行矩阵转置,依赖于shape,不能用于一维矩阵(非copy) |
| ndarray.swapaxes(xIndex,yIndex) | 交换维度(非copy) |
| 计算函数 | 说明 |
| ndarray.mean( axis=0 ) | 求平均值 |
| ndarray.sum( axis= 0) | 求和 |
| ndarray.cumsum( axis=0) ndarray.cumprod( axis=0) |
累加 累乘 |
| ndarray.std() ndarray.var() |
方差 标准差 |
| ndarray.max() ndarray.min() |
最大值 最小值 |
| ndarray.argmax() ndarray.argmin() |
最大值索引 最小值索引 |
| ndarray.any() ndarray.all() |
是否至少有一个True 是否全部为True |
| ndarray.dot( ndarray) |
计算矩阵内积 |
| 排序函数 |
说明 |
| ndarray.sort(axis=0) |
排序,返回源数据 |
表2.1.B.2 ndarray函数
| ndarray[n] | 选取第n+1个元素 |
| ndarray[n:m] | 选取第n+1到第m个元素 |
| ndarray[:] | 选取全部元素 |
| ndarray[n:] | 选取第n+1到最后一个元素 |
| ndarray[:n] | 选取第0到第n个元素 |
| ndarray[ bool_ndarray ] 注:bool_ndarray表示bool类型的ndarray |
选取为true的元素 |
| ndarray[[x,y,m,n]]... |
选取顺序和序列为x、y、m、n的ndarray |
| ndarray[n,m] ndarray[n][m] |
选取第n+1行第m+1个元素 |
| ndarray[n,m,...] ndarray[n][m].... |
选取n行n列....的元素 |
表2.1.B.3 ndarray索引/切片方式
C NumPy.random函数和属性:
| 函数 | 说明 |
| seed() seed(int) seed(ndarray) |
确定随机数生成种子 |
| permutation(int) permutation(ndarray) |
返回一个一维从0~9的序列的随机排列 返回一个序列的随机排列 |
| shuffle(ndarray) | 对一个序列就地随机排列 |
| rand(int) randint(begin,end,num=1) |
产生int个均匀分布的样本值 从给定的begin和end随机选取num个整数 |
| randn(N, M, ...) | 生成一个N*M*...的正态分布(平均值为0,标准差为1)的ndarray |
| normal(size=(N,M,...)) | 生成一个N*M*...的正态(高斯)分布的ndarray |
| beta(ndarray1,ndarray2) | 产生beta分布的样本值,参数必须大于0 |
| chisquare() | 产生卡方分布的样本值 |
| gamma() | 产生gamma分布的样本值 |
| uniform() | 产生在[0,1)中均匀分布的样本值 |
2.1.C.1 random常用函数
D NumPy.linalg函数和属性:
| 函数 | 说明 |
| det(ndarray) | 计算矩阵列式 |
| eig(ndarray) | 计算方阵的本征值和本征向量 |
| inv(ndarray) pinv(ndarray) |
计算方阵的逆 计算方阵的Moore-Penrose伪逆 |
| qr(ndarray) | 计算qr分解 |
| svd(ndarray) | 计算奇异值分解svd |
| solve(ndarray) | 解线性方程组Ax = b,其中A为方阵 |
| lstsq(ndarray) | 计算Ax=b的最小二乘解 |
2.1.D.1 linalg常用函数
附加:
numpy linalg模块
线性代数
# numpy.linalg模块包含线性代数的函数。使用这个模块,可以计算逆矩阵、求特征值、解线性方程组以及求解行列式等。
import numpy as np
1. 计算逆矩阵
创建矩阵
A = np.mat("0 1 2;1 0 3;4 -3 8")
print (A)
#[[ 0 1 2]
# [ 1 0 3]
# [ 4 -3 8]]
使用inv函数计算逆矩阵
inv = np.linalg.inv(A)
print (inv)
#[[-4.5 7. -1.5]
# [-2. 4. -1. ]
# [ 1.5 -2. 0.5]]
检查原矩阵和求得的逆矩阵相乘的结果为单位矩阵
print (A * inv)
#[[ 1. 0. 0.]
# [ 0. 1. 0.]
# [ 0. 0. 1.]]
# 注:矩阵必须是方阵且可逆,否则会抛出LinAlgError异常。
2. 求解线性方程组
# numpy.linalg中的函数solve可以求解形如 Ax = b 的线性方程组,其中 A 为矩阵,b 为一维或二维的数组,x 是未知变量
import numpy as np
#创建矩阵和数组
B = np.mat("1 -2 1;0 2 -8;-4 5 9")
b = np.array([0,8,-9])
调用solve函数求解线性方程
x = np.linalg.solve(B,b)
print (x)
#[ 29. 16. 3.]
使用dot函数检查求得的解是否正确
print (np.dot(B , x))
# [[ 0. 8. -9.]]
3. 特征值和特征向量
# 特征值(eigenvalue)即方程 Ax = ax 的根,是一个标量。其中,A 是一个二维矩阵,x 是一个一维向量。特征向量(eigenvector)是关于特征值的向量
# numpy.linalg模块中,eigvals函数可以计算矩阵的特征值,而eig函数可以返回一个包含特征值和对应的特征向量的元组
import numpy as np
# 创建一个矩阵
C = np.mat("3 -2;1 0")
# 调用eigvals函数求解特征值
c0 = np.linalg.eigvals(C)
print (c0)
# [ 2. 1.]
# 使用eig函数求解特征值和特征向量 (该函数将返回一个元组,按列排放着特征值和对应的特征向量,其中第一列为特征值,第二列为特征向量)
c1,c2 = np.linalg.eig(C)
print (c1)
# [ 2. 1.]
print (c2)
#[[ 0.89442719 0.70710678]
# [ 0.4472136 0.70710678]]
# 使用dot函数验证求得的解是否正确
for i in range(len(c1)):
print ("left:",np.dot(C,c2[:,i]))
print ("right:",c1[i] * c2[:,i])
#left: [[ 1.78885438]
# [ 0.89442719]]
#right: [[ 1.78885438]
# [ 0.89442719]]
#left: [[ 0.70710678]
# [ 0.70710678]]
#right: [[ 0.70710678]
# [ 0.70710678]]
4.奇异值分解
# SVD(Singular Value Decomposition,奇异值分解)是一种因子分解运算,将一个矩阵分解为3个矩阵的乘积
# numpy.linalg模块中的svd函数可以对矩阵进行奇异值分解。该函数返回3个矩阵——U、Sigma和V,其中U和V是正交矩阵,Sigma包含输入矩阵的奇异值。
import numpy as np
# 分解矩阵
D = np.mat("4 11 14;8 7 -2")
# 使用svd函数分解矩阵
U,Sigma,V = np.linalg.svd(D,full_matrices=False)
print ("U:",U)
#U: [[-0.9486833 -0.31622777]
# [-0.31622777 0.9486833 ]]
print ("Sigma:",Sigma)
#Sigma: [ 18.97366596 9.48683298]
print ("V",V)
#V [[-0.33333333 -0.66666667 -0.66666667]
# [ 0.66666667 0.33333333 -0.66666667]]
# 结果包含等式中左右两端的两个正交矩阵U和V,以及中间的奇异值矩阵Sigma
# 使用diag函数生成完整的奇异值矩阵。将分解出的3个矩阵相乘
print (U * np.diag(Sigma) * V)
#[[ 4. 11. 14.]
# [ 8. 7. -2.]]
5. 广义逆矩阵
# 使用numpy.linalg模块中的pinv函数进行求解,
# 注:inv函数只接受方阵作为输入矩阵,而pinv函数则没有这个限制
import numpy as np
# 创建一个矩阵
E = np.mat("4 11 14;8 7 -2")
# 使用pinv函数计算广义逆矩阵
pseudoinv = np.linalg.pinv(E)
print (pseudoinv)
#[[-0.00555556 0.07222222]
# [ 0.02222222 0.04444444]
# [ 0.05555556 -0.05555556]]
# 将原矩阵和得到的广义逆矩阵相乘
print (E * pseudoinv)
#[[ 1.00000000e+00 -5.55111512e-16]
# [ 0.00000000e+00 1.00000000e+00]]
6. 行列式
# numpy.linalg模块中的det函数可以计算矩阵的行列式
import numpy as np
# 计算矩阵的行列式
F = np.mat("3 4;5 6")
# 使用det函数计算行列式
print (np.linalg.det(F))
# -2.0