KNN SVM Softmax 在 CIFAR-10上的图像识别

概述

这篇博客以CIFAR-10数据集为基础，从对图像识别基础的预处理部分分析其背后理论，到讲述对KNN SVM Softmax的具体实现，并通过验证集进行参数调优，最后展开结果性分析，介绍基本的图像识别应用，材料部分来自于Stanford CS231n 的notes和assignments(project)。

CIFAR-10介绍

该数据集共有60000张彩色图像，每张图像是32*32*3的像素，相对较小且不需要分割提取的过程，可以直接进行处理，分为10个类，每类6000张图。这里面有50000张用于训练，构成了5个训练批，每一批10000张图；另外10000用于测试，单独构成一批。测试批的数据里，取自10类中的每一类，每一类随机取1000张。抽剩下的就随机排列组成了训练批。

如果是从CS231n提供的框架中下载的数据集，在Linux环境下只需要运行get_datasets.sh，为方便处理文件是以16进制存储的

这里对图像的提取不做赘述

上面就是从数据集中抽取的部分图片，可以看出就算一个类别内但彼此的差异性还是比较大的。抽取部分图片并展示的代码：

classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):
    idxs = np.flatnonzero(y_train == y)
    idxs = np.random.choice(idxs, samples_per_class, replace=False)
    for i, idx in enumerate(idxs):
        plt_idx = i * num_classes + y + 1
        plt.subplot(samples_per_class, num_classes, plt_idx)
        plt.imshow(X_train[idx].astype('uint8'))
        plt.axis('off')
        if i == 0: 

plt.title(cls)；plt.show()

KNN进行图像识别

应该说，KNN是最为直观的识别算法，也易于实现，值得一提的是，我记得上次有同学在课程上尝试用《机器学习实战》书上的代码进行手写字识别，但是运行时间实在太长，其实虽然KNN是一种很耗费计算资源且如果数据维数变高后会变得十分恐怖的算法，但在面对大量数据时依旧可以通过矩阵化的计算极大地优化计算。

首先，对图像进行预处理，将我们32*32*3的每个图像化成一行，并且由于KNN并不是我们今天的主角且耗时较大，我们没有用全部的数据集进行训练，抽取了5000张数据集和500张测试集进行实验，目的是为了与SVM Softmax进行比较。

下面提供KNN代码，用类封装：

import numpy as np
class KNearestNeighbor(object):

  def __init__(self):
    pass

  def train(self, X, y):
    self.X_train = X
    self.y_train = y
   
  def predict(self, X, k=1, num_loops=0):
    if num_loops == 0:
      dists = self.compute_distances_no_loops(X)
    elif num_loops == 1:
      dists = self.compute_distances_one_loop(X)
    elif num_loops == 2:
      dists = self.compute_distances_two_loops(X)
    else:
      raise ValueError('Invalid value %d for num_loops' % num_loops)

    return self.predict_labels(dists, k=k)

  def compute_distances_two_loops(self, X):
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    for i in range(num_test):
      for j in range(num_train):
        dists[i][j] = np.linalg.norm(X[i, :] - self.X_train[j, :])
    return dists

  def compute_distances_one_loop(self, X):
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    for i in range(num_test):
      dists[i,:] = np.linalg.norm(self.X_train - X[i,:], axis=1)
    return dists

  def compute_distances_no_loops(self, X):
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train)) 
    dists = np.multiply(np.dot(X, self.X_train.T),-2) 
    sq1 = np.sum(np.square(X),axis=1,keepdims = True) 
    sq2 = np.sum(np.square(self.X_train),axis=1) 
    dists = np.add(dists,sq1) 
    dists = np.add(dists,sq2) 
    dists = np.sqrt(dists)  
    return dists

  def getNormMatrix(self, x, lines_num):
    return np.ones((lines_num, 1)) * np.sum(np.square(x), axis = 1)

  def predict_labels(self, dists, k=1):
    num_test = dists.shape[0]
    y_pred = np.zeros(num_test)
    for i in range(num_test):
      # A list of length k storing the labels of the k nearest neighbors to
      # the ith test point.
      # closest_y = []
      closest_y = self.y_train[dists[i, :].argsort()[: k]]
      y_pred[i] = np.argmax(np.bincount(closest_y))
    return y_pred

CS231n给出了框架，具体算法实现我已经自己完成，可以看到，在训练数据时运用了三种方式，一个是完全依靠循环，然后是半矩阵化最后是完全矩阵化，完全矩阵化的过程没有那么直观，需要用到相关公式，推导部分可以参考https://blog.csdn.net/geekmanong/article/details/51524402 

 

这种优化的方法也就是函数compute_distances_no_loops(self, X)所实现的。

实验中给出一个很有意思的可视化，我们对500个测试集与训练集的L2距离存储并且通过python imshow()的方式展示，那么我们得到了这样一张图：

纵坐标[0, 500]是测试集id，与[0,5000]的测试集进行比较，颜色的深浅代表了图像之间的L2距离大小，我们可以看到，虽然结果较为随机，但是有明显的横条与竖条带的存在，也就是意味着，这张训练图或者测试图，与所有的侧视图或者训练图的差别都很大，其实这个可视化结果，也一方面说明了KNN算法的不准确性。

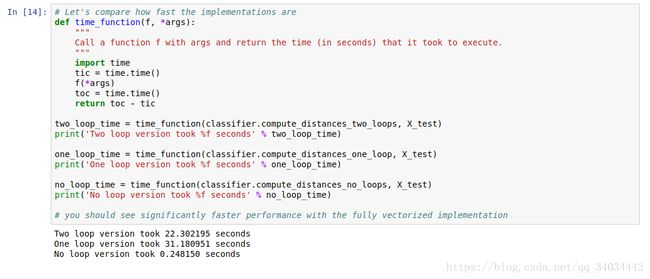
在Juyter notebook上我们进一步的展示完全依靠循环、半矩阵化和完全矩阵化算法的效率比较：

计算时间差大概有100多倍，也就解释了上次同学跑手写字识别为了么用了很久跑不出。

进一步的，我们对KNN进行了交叉验证，选取最优的K值：

num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]

X_train_folds = []
y_train_folds = []
y_train_ = y_train.reshape(-1, 1)
X_train_folds , y_train_folds = np.array_split(X_train, 5), np.array_split(y_train_, 5)
k_to_accuracies = {}
for k_ in k_choices:
    k_to_accuracies.setdefault(k_, [])
for i in range(num_folds):
    classifier = KNearestNeighbor()
    X_val_train = np.vstack(X_train_folds[0:i] + X_train_folds[i+1:])
    y_val_train = np.vstack(y_train_folds[0:i] + y_train_folds[i+1:])
    y_val_train = y_val_train[:,0]
    classifier.train(X_val_train, y_val_train)
    for k_ in k_choices:
        y_val_pred = classifier.predict(X_train_folds[i], k=k_)
        num_correct = np.sum(y_val_pred == y_train_folds[i][:,0])
        accuracy = float(num_correct) / len(y_val_pred)
        k_to_accuracies[k_] = k_to_accuracies[k_] + [accuracy]
for k in sorted(k_to_accuracies):
    for accuracy in k_to_accuracies[k]:
        print('k = %d, accuracy = %f' % (k, accuracy))

并绘制了不同k的结果图：

最终选取了k=10

最后，我们的预测准确率为28%左右，考虑到这是一个10分类问题，其实KNN算法还是有一定效果的。

 

SVM vs Softmax

CS229中对支持向量机进行了详细的推到，我之前博客中也对细节进行了阐释，从开始的函数间隔到优化试再到SMO算法，刚开始我以为这整个一套推论就是支持向量机的核心思想，但这次我们构造了多分类的支持向量机（Multiclass Support Vector Machine），感觉对支持向量机有了更深的理解。

为了进一步介绍，我们先来看为了使用SVM和Softmax，我们定义的图像识别方法：

这里我们的思想是：对每一个分类构造一个权重系数W和b使其能够对输入的x_i进行打分，然后选取分数最高的作为我们的分类结果，还是比较直观的，即：

$$f(x_i, W, b) =  W x_i + b$$

而我们的目标就是使用特定的方法来优化这个系数W和b。

那么，为了能够量化每组系数的优劣程度，我们来定义一个量：损失函数（Loss Function）。通过损失函数定量分析系数的好坏是进一步优化的基础。这里我们就要开始分析这里的SVM和CS229的不同和SVM与Softmax的区别。

我现在的理解是（理解不到位处欢迎指正）支持向量机真正的核心，不是从定义了函数间隔到SMO算法那一整套东西，而是从最初开始本质的损失函数定义：

这张图其实是似曾相识的，在CS229定义的那个形式中，我们导出了最初的优化试再通过拉格朗日法SMO进行求解，而在图像识别时，我们用到的是SVM最本质的损失定义方式，而不是后面的求解方法，因此我们的求解方法也因问题的不同而不同。

那么下面给出我们图像识别时，运用SVM思想给出的损失函数：

$$L_i = \sum_{j\neq y_i} \max(0, s_j - s_{y_i} + \Delta)$$

$$s_j = f(x_i, W)_j$$

也即是：

$$L_i = \sum_{j\neq y_i} \max(0, w_j^T x_i - w_{y_i}^T x_i + \Delta)$$

要理解这个式子，就要结合上面那张折线图，在我通过系数W和b对一张图给所有类打分后，只有正确的类的分数比其他类更高，我们才能正确的分类，公式里的s其实就是打分的分数，即，我们计算所有类的分数与正确类的分数差加上delta（就是那个三角）的和作为损失函数，当正确的类分数比其他类高delta以上，那么损失就是0，否则按上面的式子计算损失。

给了上面的理解，我们进一步引出Softmax的损失函数式，它与SVM的区别是，从信息论的角度定义了损失函数：

$$L_i = -\log\left(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} }\right) \hspace{0.5in} \text{or equivalently} \hspace{0.5in} L_i = -f_{y_i} + \log\sum_j e^{f_j}$$

f_j也就是第j类的分数。

信息论角度理解：

一个真实分布和估计分布的交叉熵定义为：

$$H(p,q) = - \sum_x p(x) \log q(x)$$

那么我们Softmax定义的损失函数目标就是尽量减少估计与真实分布的交叉熵。

 

优化

当我们成功定义了损失函数，下面要做的就是针对选择的损失函数实施相应的优化策略：

首先对原来的式稍加改进，并对图像进行预处理：

同时存在多为系数W和一维系数b非常不方便，首先，我们将W系数多加一维，相应的，输入x_i的后面加一个1，这也是机器学习中的常用策略：

$$f(x_i, W) =  W x_i$$

就是说x_i从原来的[3072*1]（32*32*3）到[3073*1] W是[10 x 3073] 替换了[10 x 3072]。

归一化：

一句话，将图像的值归一化到 [-1,1]，这个策略是服务于最终的梯度下降优化策略的。

CS231n的notes中，为了介绍最终的梯度下降策略，首先讲了两个比较佛系的策略，第一种是多次随机生成W（random search）记下其中最好的，这种方法有15%的准确率，另一种是随机局部搜索（Random Local Search）这种方法有20%的正确率，考虑到这是一个10分类的问题，这种随机的算法已经有点进步了。

最后带来了我们的梯度下降策略，就是对损失函数求导将W向导数方向改变：

先说SVM，对原始进行求导得到:

原式：

$$L_i = \sum_{j\neq y_i} \max(0, w_j^T x_i - w_{y_i}^T x_i + \Delta)$$

注意原式条件，这个求导过程需注意条件分类讨论，当j == y_i时：

$$\nabla_{w_{y_i}} L_i = - \left( \sum_{j\neq y_i} \mathbb{1}(w_j^Tx_i - w_{y_i}^Tx_i + \Delta > 0) \right) x_i$$

当j != y_i时：

$$\nabla_{w_j} L_i = \mathbb{1}(w_j^Tx_i - w_{y_i}^Tx_i + \Delta > 0) x_i$$

实现时，cs231notes要求实现不同程度矩阵化的算法，这里给出完全矩阵化的代码并给出比较结果：

def svm_loss_vectorized(W, X, y, reg):

  """
  Structured SVM loss function, vectorized implementation.

  Inputs and outputs are the same as svm_loss_naive.
  """
  loss = 0.0
  dW = np.zeros(W.shape) # initialize the gradient as zero

  #############################################################################
  # TODO:                                                                     #
  # Implement a vectorized version of the structured SVM loss, storing the    #
  # result in loss.                                                           #
  #############################################################################
  num_train = X.shape[0]
  delta = 1
  scores = X.dot(W)
  margins = np.maximum(0, scores - scores[np.arange(num_train), y].reshape(-1,1) + delta)
  margins[np.arange(num_train), y] = 0
  loss = np.sum(margins)
  loss /= num_train
  loss += 0.5 * reg * np.sum(W*W) # regularization

  #############################################################################
  #                             END OF YOUR CODE                              #
  #############################################################################
  #############################################################################
  # TODO:                                                                     #
  # Implement a vectorized version of the gradient for the structured SVM     #
  # loss, storing the result in dW.                                           #
  #                                                                           #
  # Hint: Instead of computing the gradient from scratch, it may be easier    #
  # to reuse some of the intermediate values that you used to compute the     #
  # loss.                                                                     #
  #############################################################################
  gradient = np.zeros(margins.shape)
  gradient[margins>0] = 1
  wrong_count = gradient.sum(axis=1)
  gradient[np.arange(num_train), y] = -wrong_count
  dW = X.T.dot(gradient) # cool!
  dW /= num_train
  dW += reg*W

可见矩阵化后与非矩阵化结果相同但快了约30倍。

下面进行实际的优化过程：

采用Stochastic Gradient Descent，即每次迭代不用全部的训练集作为训练而是抽取部分样本，进行多次迭代，为了验证算法的有效性，我们绘制了损失函数曲线进行可视化分析：

可以看出算法能够较为有效的降低损失函数。

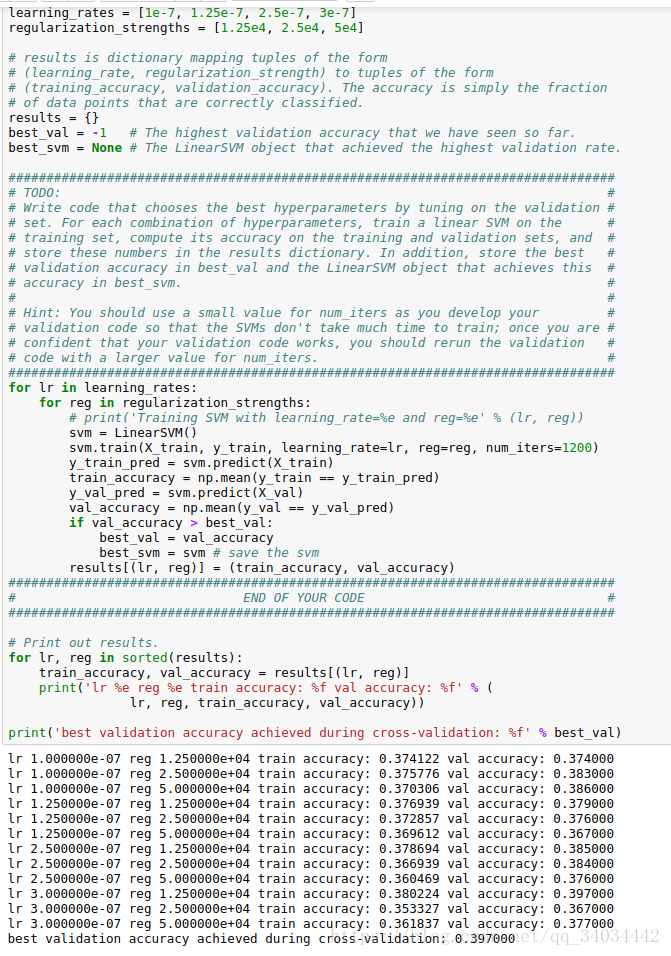
接着通过validation set 对每次优化的步长learning rate和归一化系数reg进行优化，直接截取jupyter notebook 结果：

同时对参数选择进行可视化分析：

在这张图上，颜色越淡的点就准确度越高。

这个调优后的结果在测试集上达到了36.9%的准确度。

最后，我们通过svm训练的模型一种理解方式就是训练出待识别的某种物体的模板，因此在我们的模型训练完毕后，还可以将其绘出，应该能够一定程度反应待识别物体的形状。

下面是实验训练的模型的绘图结果：

图片中能依稀看到物体的形状，但是当我们看马的训练图时，感觉上有两个头，这是因为实际的训练图片中给的马头部的朝向是两个都有的。

Softmax

同样，我们通过Softmax进行训练。在实际实现中,是将softmax和SVM共同继承LinearClassifier类的，因为二者的共同运用了对权重进行优化的思想，差别在于定义的损失函数不同。

我们重新给出Softmax的损失函数：

$$L_i = -\log\left(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} }\right) \hspace{0.5in} \text{or equivalently} \hspace{0.5in} L_i = -f_{y_i} + \log\sum_j e^{f_j}$$

对其进行求导：

$$\left\{\begin{aligned}\nabla_{w_{y_i}} L_i = & -x_i + \frac{e^{f_{y_i}}}{\sum_j e^{f_j}} x_i & j = y_i \\\nabla_{w_j} L_i = &\frac{e^{f_j}}{\sum_j e^{f_j}} x_i & j \ne y_i\end{aligned}\right.$$

代码同样需要对其进行矩阵化计算，这里省去和SVM重复步骤的说明，直接分析最后结果，识别准确度在35.5%

也将模型可视化：

引用

[1] lecture notes, assignments of CS231n Standford University. http://cs231n.stanford.edu/syllabus.html

[2] 矩阵梯度求解参考 https://blog.csdn.net/pjia_1008/article/details/66972060