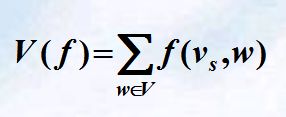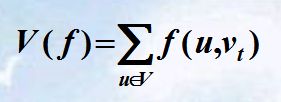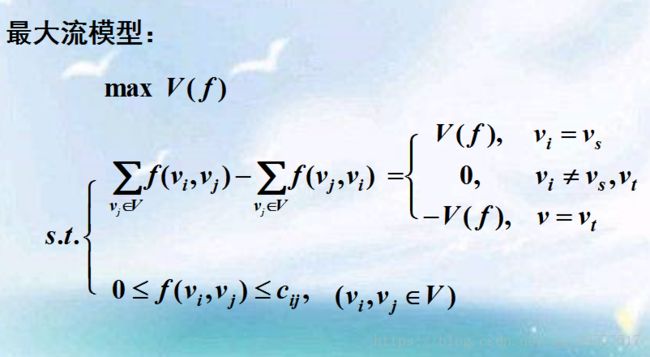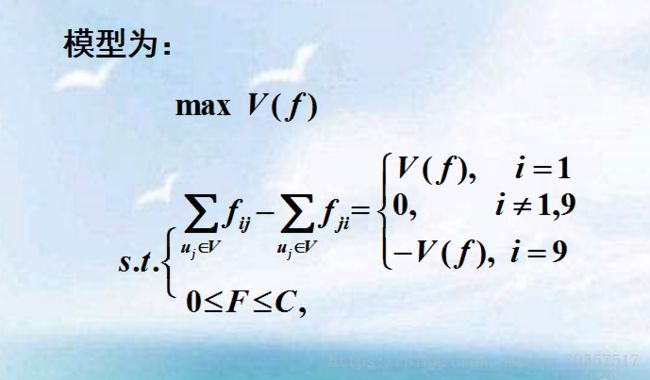最大流问题讲解（Lingo）
第一节 图论的基本知识
1. 图的概念
定义 图G(V,E)是指一个二元组(V(G),E(G))，其中:
(1)V(G)={v1,v2,…, vn}是非空有限集，称为顶点集，
(2)E(G)是V(G)中的元素对(vi,vj)组成的集合称为边集。
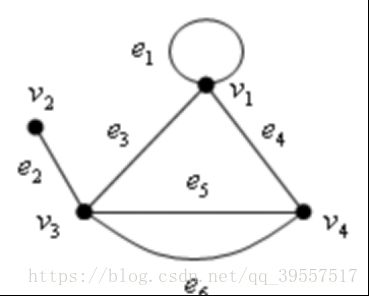
图G：V(G)={v1,v2,v3,v4}
E(G)= {e1,e2,e3,e4,e5,e6}
e3=(v1,v3)
若图G的边是有方向的，称G是有向图，有向图的边称为有向边或弧。
常用术语
边和它的两端点称为互相关联.
与同一条边关联的两个端点称为相邻的顶点，
与同一个顶点关联的两条边称为相邻的边.
3)端点重合为一点的边称为环.
4) 若一对顶点之间有两条以上的边联结，
则这些边称为重边．
5)既没有环也没有重边的图，称为简单图．
6) 若图G的每一条边e 都赋以一个实数w(e)，
称w(e)为边e的权，
G连同边上的权称为赋权图 ,
记为：G(V,E,W)， W={w(e)| e∈E}
7) 图G的中顶点的个数， 称为图G的阶；
图中与某个顶点相关联的边的数目，称为该顶点的度。
8）完全图：若无向图的任意两个顶点之间都存在着一条边，
称此图为完全图。
2.图的矩阵表示
邻接矩阵: (以下均假设图为简单图).
图G的邻接矩阵是表示顶点之间相邻关系的矩阵：A=(aij)，
其中：
无向图G
邻接矩阵
A=(aij)
有向图G
邻接矩阵
A=(aij)
第二节 最大流问题
定义：设G(V,E)为有向图，若在每条边e上定义一个非负权c，
则称图G为一个网络，称c为边e的容量函数，记为c(e)。
若在有向图G(V,E)中有两个不同的顶点vs与vt ，
若顶点vs只有出度没有入度，称vs为图G的源，
若顶点vt只有入度没有出度，
称vt为G的汇，
若顶点v 既不是源也不是汇，
称为v中间顶点。
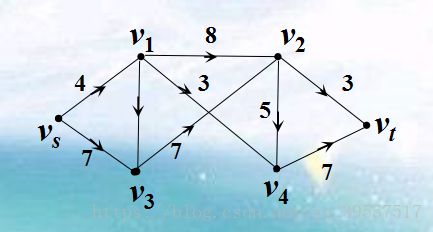
设u,v是网络G(V,E)的相邻顶点，边(u,v)上定义的函数f(u,v)
称为边(u,v)上的实际流量（ u到v的流量 ）；
若对网络G(V,E)的任意相邻顶点u,v 均成立： 0≤ f(u,v) ≤ c(u,v) ，
称该网络为相容网络。
若v为网络G(V,E)的中间顶点，
有：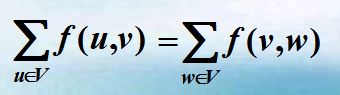
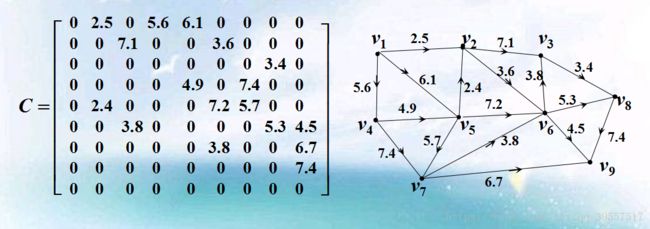
网络的总流量为从源vs 流出的总流量：
流入汇vt 总流量：
例1 分组交换技术在计算机网络中发挥着重要作用，信息从源节点到目的节点不再需要一条固定的路径，而是将其分割为几组，通过不同的路径传输到目的节点，目的节点再重新组合还原文件。现考察如图所示的网络，图中两节点间的数字表示两交换机间可用的带宽，此时从节点1到节点9的最大带宽为多少？
设fij为从vi到vj的实际流量，得一个9阶方阵：F=( fij)
记容量矩阵为：
Lingo代码：
sets: node/v1..v9/;
arc(node,node):c,f;
endsets
[OBJ]max=flow;
@for(node(i)|i#ne#1#and#i#ne#9:@sum(node(j):f(i,j))=@sum(node(j):f(j,i)));
@sum(node(j): f(1,j))=flow;
@sum(node(j): f(j,9))=flow;
@for(arc:@bnd(0,f,c));
data:
c=
0 2.5 0 5.6 6.1 0 0 0 0
0 0 7.1 0 0 3.6 0 0 0
0 0 0 0 0 0 0 3.4 0
0 0 0 0 4.9 0 7.4 0 0
0 2.4 0 0 0 7.2 5.7 0 0
0 0 3.8 0 0 0 0 5.3 4.5
0 0 0 0 0 3.8 0 0 6.7
0 0 0 0 0 0 0 0 7.4
0 0 0 0 0 0 0 0 0;
@text()=@table(f);
enddataLingo基础：
//图片中比较抽象，下面我用C语言的结构体类比一下
/*
集 ←→ 结构体
集成员 ←→ 结构体的域
集属性 ←→ 结构体实例
*/
struct person {//person 相当于 setname
//sex, age 相当于集成员
char sex;
int age;
};
struct person xiaoming;//小明相当于成员属性
xiaoming.sex = 'M';
xiaoming.age = 20;
#ne# not equal（不等于）若两边运算值不相等，返回逻辑值为1；
否则返回逻辑值为0;
#and# 仅当两边的参数都为1时，结果为1；
@bnd(L,x,U) 限制L≤x≤U
1．@for
该函数用来产生对集成员的约束。基于建模语言的标量需要显式输入每个约束，不过@for函数允许只输入一个约束，然后LINGO自动产生每个集成员的约束。
例4.10 产生序列{1,4,9,16,25}
model:
sets:
number/1..5/:x;
endsets
@for(number(I): x(I)=I^2);
end
2．@sum
该函数返回遍历指定的集成员的一个表达式的和。
例4.11 求向量[5，1，3，4，6，10]前5个数的和。
model:
data:
N=6;
enddata
sets:
number/1..N/:x;
endsets
data:
x = 5 1 3 4 6 10;
enddata
s=@sum(number(I) | I #le# 5: x);
end答案：
