单调栈模拟(入门)
例题
PKU 3250
牛客 小A的柱状图
HDU 1506
利用单调栈,可以找到从左/右遍历第一个比它小/大的元素的位置
举个例子:
假设有一个单调递增的栈 S和一组数列:
a : 5 3 7 4
用数组L[i] 表示 第i个数向左遍历的第一个比它小的元素的位置
如何求L[i]?
首先我们考虑一个朴素的算法,可以按顺序枚举每一个数,然后再依此向左遍历。
但是当数列单调递减时,复杂度是严格的O(n^2)。
此时我们便可以利用单调栈在O(n)的复杂度下实现
我们按顺序遍历数组,然后构造一个单调递增栈
(1). i = 1时,因栈为空,L[1] = 0,此时再将第一个元素的位置下标1存入栈中
此时栈中情况:

(2).i = 2时,因当前3小于栈顶元素对应的元素5,故将5弹出栈
此时栈为空
故L[2] = 0
然后将元素3对应的位置下标2存入栈中
此时栈中情况:
(3).i = 3时,因当前7大于栈顶元素对应的元素3,故
L[3] = S.top() = 2 (栈顶元素的值)
然后将元素7对应的下标3存入栈
此时栈中情况:
(4).i = 4时,为保持单调递增的性质,应将栈顶元素3弹出
此时 L[4] = S.top() = 2;
然后将元素4对应的下标4存入栈
此时栈中情况:
至此 算法结束
对应的结果:
a : 5 3 7 4
L : 0 0 2 2
题一:
PKU 3250
题目链接
很裸的单调栈,而且只需要跑一个方向。
简单入门题
给n个牛的身高,从左往右站成一排,集体向右看,能看到比自己矮的牛的个数,一旦有一个比他高,那么右边的全部被挡住视线了。
思路:从右向左遍历,栈顶的牛比当前高,当前能看到的数量为0,入栈。栈顶的牛比自己低,加1加上栈顶的牛能看到的数量
#include
#include
#include
using namespace std;
typedef long long ll;
const int N=8e4+10;
ll a[N],sum[N],ans;
stackque;
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
que.push(n+1);
a[n+1]=1e18;
for(int i=n;i>=1;i--){
if(a[i]>a[que.top()])
{
ll t=0;
while(a[i]>a[que.top()])
{
t+=sum[que.top()]+1;
que.pop();
}
sum[i]=t;
que.push(i);
}
else
{
sum[i]=0;
que.push(i);
}
}
ll ans=0;
for(int i=1;i<=n;i++) ans+=sum[i];
printf("%lld\n",ans);
} 题二:
链接:https://ac.nowcoder.com/acm/contest/549/H
来源:牛客网
小A的柱状图
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
柱状图是有一些宽度相等的矩形下端对齐以后横向排列的图形,但是小A的柱状图却不是一个规范的柱状图,它的每个矩形下端的宽度可以是不相同的一些整数,分别为a[i]a[i],每个矩形的高度是h[i]h[i],现在小A只想知道,在这个图形里面包含的最大矩形面积是多少。
输入描述:
一行一个整数N,表示长方形的个数
接下来一行N个整数表示每个长方形的宽度
接下来一行N个整数表示每个长方形的高度输出描述:
一行一个整数,表示最大的矩形面积示例1
输入
复制
7
1 1 1 1 1 1 1
2 1 4 5 1 3 3输出
复制
8说明
样例如图所示,包含的最大矩形面积是8备注:
1≤n≤1e6,1≤a[i]≤100,1≤h[i]≤1e9
#include
using namespace std;
typedef long long ll;
const int N=1e6+10;
ll sum[N],a[N],h[N],l[N],r[N],ans;
int n;
stackque;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),sum[i]=sum[i-1]+a[i];
for(int i=1;i<=n;i++) scanf("%d",&h[i]);
que.push(0);
que.push(1);
l[1]=a[1];
for(int i=2;i<=n;i++)
{
while(h[i]<=h[que.top()])
{
que.pop();
}
l[i]=sum[i]-sum[que.top()];
que.push(i);
}
while(que.size())que.pop();
que.push(n+1);
que.push(n);
r[n]=a[n];
h[n+1]=0;
for(int i=n-1;i>=1;i--)
{
while(h[i]<=h[que.top()])
{
que.pop();
}
r[i]=sum[que.top()-1]-sum[i-1];
que.push(i);
}
ll ans=0;
for(int i=1;i<=n;i++)
ans=max(ans,h[i]*(l[i]+r[i]-a[i]));
cout<
题三:
这个跟上面那个题类似,少了一行矩形宽度的输入,还简单些
Largest Rectangle in a Histogram
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 26083 Accepted Submission(s): 8214
Problem Description
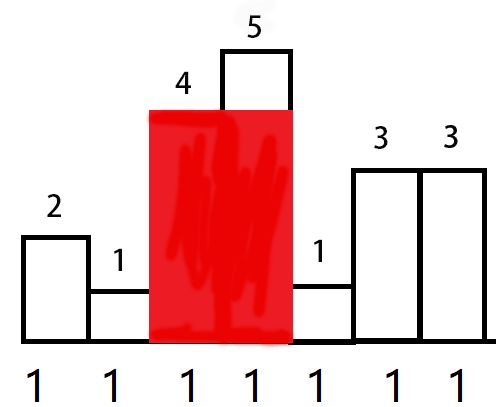
A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:![]()
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.
Input
The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, ..., hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.
Output
For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.
Sample Input
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000 0
Sample Output
8
4000
Source
University of Ulm Local Contest 2003
Recommend
LL
以下来自 https://blog.csdn.net/wubaizhe/article/details/70136174
首先考虑最大面积的矩形X的左右边界的性质:
设其左边界为L,右边界为R,则其高H = min{h[i] | L <= i <= R}
此时最大面积为 (R - L + 1) * H
若此时左边界的左边那个矩形的高度 h[L-1] >= H
则左边界可以向左拓展,则新的面积为:
(R - (L-1) + 1) * H > 原面积
则与原假设条件冲突
故左边界左边的那个矩形的高度 :h[L-1] < H
同理右边界右边的那个矩形的高度: h[R+1] < H
设H = h[i]
所以左边界L是满足h[j-1] < h[i]的最大的j,即从i点向左遍历的第一个高度比i小的点的右边一个点
而右边界R是满足 h[j+1] < h[i]的最小的j,即从i点向右遍历第一个高度比i小的点的左边一个点
所以我们可以利用单调栈的性质得到每个确定点,即确定高度的最大面积矩形的左右边界,然后枚举取最大即可。
#include
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define rep(i, a, b) for(int i(a); i <= (b); ++i)
#define dec(i, a, b) for(int i(a); i >= (b); --i)
#define MP make_pair
const int N = 100000 + 100;
stack S;
ll h[N];
int R[N],L[N];
int main(){
int n;
while(~scanf("%d",&n) && n){
for(int i=0 ;i= h[i]) S.pop();
if(S.empty()) L[i] = 0;
else L[i] = S.top() + 1;
S.push(i);
}
while(S.size()) S.pop();
for(int i=n-1 ;i>=0 ;i--){
while(S.size() && h[S.top()] >= h[i]) S.pop();
if(S.empty()) R[i] = n;
else R[i] = S.top();
S.push(i);
}
ll ans = 0;
for(int i=0 ;i