无向有环图的最长路径算法
一、问题描述
前两天一个学金融的小伙伴找我帮忙写计算机课的作业,因为英语不好,以为是让求两点间的最大路径,之前自己实现过dijkstra算法,觉得可能不难就答应了。但是只想到了用穷举法枚举出所有路径的笨方法
二、思路阐述
既然是图,就要先把图的关系表示出来,咱们用Vertex.java来表示结点,结点维护着与它相连的边,Edge.java来表示边,GraphInterface接口来规范一些模板方法。LifetimeGraph.java来实现具体查找最长路径的代码。在LifetimeGraph中,首先是添加结点和边的方法,然后是查找两点间最大路径的方法。该方法先找出两点间的所有路径,使用了递归,然后在所有路径中找出最长的。
Vertex.java:
import java.util.HashMap;
/**
* Vertex Class
*
* A vertex in the graph.
* Stores the id of the vertex and the edges.
*
* Eg. if this is Vertex1 and it connects to Vertex2
* this.edges[2] == edge between V1 and V2.
*/
/**
* The vertex class holds the "id" of the vertex and the
* edges connected.
*
* To be inserted into the graph.
*/
public class Vertex {
private int id;
private HashMap edges;
/**
* Initialises the vertex and the empty set of edges.
* @param id: the vertex ID.
*/
public Vertex(int id) {
this.id = id;
this.edges = new HashMap<>();
}
/**
* Get the vertex ID.
* @return - The id of the vertex.
*/
public int getId() {
return this.id;
}
/**
* Return the edges for this node.
* @return: The map of edges for this node.
*/
public HashMap getEdges() {
return this.edges;
}
/**
* Return the edge from this vertex to the given
* vertex if exists.
* @param v (Vertex class) - The destination for the edge.
* @return: The edge to the vertex or null.
*/
public Edge getEdgeTo(Vertex v) {
return this.edges.get(v.getId());
}
/**
* Add the edge to the "Adjacency List"
* @param v: The vertex this edge is connected to.
* @param e: The edge between this vertex and the given vertex.
*/
public void addEdge(Vertex v, Edge e) {
this.edges.put(v.getId(), e);
}
}
Edge.java
/**
* Edge Class
*
* Provides the "lifetime" between two vertices
* that are in a graph.
*/
/**
* Edge class holds the lifetime between two vertices.
*/
public class Edge {
private Vertex a;
private Vertex b;
private int lifetime;
/**
* Initialises the edge with two vertices
* @param a - The vertex to connect the edge to.
* @param b - The vertex to connect the edge to.
* @param lifetime - The lifetime between two vertices
*/
public Edge(Vertex a, Vertex b, int lifetime) {
this.a = a;
this.b = b;
this.lifetime = lifetime;
}
/**
* ***DO NOT CHANGE***
* ToString method, allows the edge to be printed in the results.
* @return String representation of the edge.
*/
public String toString() {
return String.format("V%s-%d-V%s", this.a.getId(), this.lifetime, this.b.getId());
}
/**
* Gets the lifetime of the edge.
* @return - The lifetime of the edge.
*/
public int getLifetime() {
return lifetime;
}
/**
* Return the vertex A of the edge.
* @return vertex A
*/
public Vertex getA() {
return a;
}
/**
* Return the vertex B of the edge.
* @return vertex B
*/
public Vertex getB() {
return b;
}
}
LifetimeGraph.java
import com.sun.deploy.util.ArrayUtil;
import org.omg.IOP.CodeSets;
import java.util.*;
/**
* Lifetime Graph
*
* Holds a graph of vertices where the edges between vertices has a lifetime.
* The graph is implemented using an adjacency list.
*/
/**
* The lifetime graph to implement.
*
* Implement the methods for adding an edge, getting the edge set and
* finding the lifetime path.
*/
public class LifetimeGraph implements GraphInterface {
private HashMap adjacencyList;
/**
* Initialises the grpah with an empty adjacency list.
*/
public LifetimeGraph() {
this.adjacencyList = new HashMap<>();
}
/**
* Add an edge to the graph between the given vertices (a, b)
*
*
* If the vertex doesn't exist, then create the vertex and add it to
* the adjacency list.
*
* @param a: Vertex A ID
* @param b: Vertex B ID
* @param lifetime: Lifetime of the edge.
*/
@Override
public void addEdge(int a, int b, int lifetime) {
Vertex vertex_a = adjacencyList.get(a);
Vertex vertex_b = adjacencyList.get(b);
//如果a不存在,创建a
if(vertex_a == null) {
vertex_a = new Vertex(a);
adjacencyList.put(a, vertex_a);
}
//如果b不存在,创建b
if(vertex_b == null) {
vertex_b = new Vertex(b);
adjacencyList.put(b, vertex_b);
}
Edge edgeTo = vertex_a.getEdgeTo(vertex_b);
if(edgeTo == null) {
vertex_a.addEdge(vertex_b, new Edge(vertex_a, vertex_b, lifetime));
vertex_b.addEdge(vertex_a, new Edge(vertex_b, vertex_a, lifetime));
} else {
edgeTo.setLifetime(lifetime);
}
}
private Integer[] setToArray(Set values) {
Iterator iterator1 = values.iterator();
Integer[] integers = new Integer[values.size()];
int i = 0;
while(iterator1.hasNext()) {
integers[i] = iterator1.next();
i++;
}
Arrays.sort(integers);
return integers;
}
/**
* Return the set of edges in the graph
*
* The edges should be returned in order of vertices,
* e.g. loop through vertices from 0-N.
*
* @return: List of edges in the graph.
*/
@Override
public Edge[] edges() {
Set set = adjacencyList.keySet();
Integer[] integers = setToArray(set);
int i = 0;
LinkedList linkedList = new LinkedList<>();
for(i = 0; i < integers.length; i++) {
int node = integers[i];
Vertex vertex = adjacencyList.get(node);
HashMap edges = vertex.getEdges();
Set integers1 = edges.keySet();
Integer[] integers2 = setToArray(integers1);
for(int j = 0; j < integers2.length; j++) {
if(integers2[j] > node) {
linkedList.addLast(vertex.getEdgeTo(adjacencyList.get(integers2[j])));
}
}
}
Edge[] edges1 = linkedList.toArray(new Edge[linkedList.size()]);
return edges1;
}
/**
* Return a maximum lieftime path between two vertices.
*
* @param start: (int) The ID of vertex A to begin the path.
* @param end: (int) The ID of vertex B to end the path.
* @return: The list of edges that create the path.
*/
@Override
public Edge[] lifetimePath(int start, int end) {
LinkedList> allPaths = new LinkedList<>();
LinkedList list = new LinkedList<>();
addPath(allPaths, list, start, end);
return findMaxLifeTimePath(allPaths);
}
//采用递归的方法进行枚举,由于是递归,所以是深度优先遍历,但是遍历的过程中要检测结点是否已经被加入了路径当中
public void addPath(LinkedList> allPaths, LinkedList path, Integer node, Integer end) {
path.add(node);//当前的path包含着根节点,即起点,path还有一个作用,就是用来检测下一个要加入的结点在路径中是否已经包含
if(node == end) {//当遇到要达到的那个结点时,递归就结束了,只需要把路径加入到所有路径的list中
allPaths.add(path);
} else {
Vertex vertex = adjacencyList.get(node);
HashMap edges = vertex.getEdges();
Set integers = edges.keySet();
Iterator iterator = integers.iterator();
while (iterator.hasNext()) {
Integer next = iterator.next();
if(path.contains(next)) {
continue;
}
addPath(allPaths, new LinkedList<>(path), next, end);
}
}
}
//这个方法用来查找所有路径中最长的那一条
private Edge[] findMaxLifeTimePath(LinkedList> allPaths) {
Iterator> iterator = allPaths.iterator();
LinkedList max = null;
int maxLifeTime = 0;
while (iterator.hasNext()) {
// int sum = -1 >>> 1;
int sum = 0;
LinkedList next = iterator.next();
LinkedList next2 = new LinkedList<>();
next2.addAll(next);//不修改原有创建好的路径
//往下的代码很简单,就是计算出该路径的长度,判断是否是最长的
Integer pop = next.pop();
while(!next.isEmpty()) {
Integer pop1 = next.pop();
Vertex vertex = adjacencyList.get(pop);
Edge edgeTo = vertex.getEdgeTo(adjacencyList.get(pop1));
int lifetime = edgeTo.getLifetime();
sum += lifetime;
pop = pop1;
}
if(sum > maxLifeTime) {
// if(sum > maxLifeTime || max.size() > next2.size()) {
maxLifeTime = sum;
max = next2;
}
}
Edge[] edges = new Edge[max.size()-1];
int i = 0;
Integer pop = max.pop();
while(!max.isEmpty()) {
Integer pop1 = max.pop();
Vertex vertex = adjacencyList.get(pop);
Edge edgeTo = vertex.getEdgeTo(adjacencyList.get(pop1));
pop = pop1;
edges[i++] = edgeTo;
}
return edges;
}
}
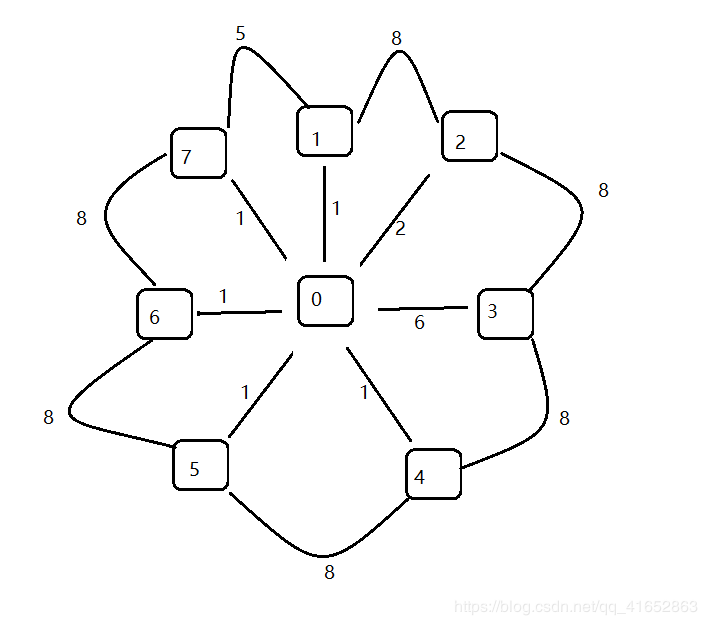
测试:咱们就用这个例子来测试
先手动构建出来这个图表达的关系:
public class Main {
public static void main(String[] args) {
LifetimeGraph lifetimeGraph = new LifetimeGraph();
/**
* V0-1-V1 V0-2-V2 V0-6-V3 V0-1-V4 V0-1-V5
* V0-1-V6 V0-1-V7 V1-8-V2 V1-5-V7 V2-8-V3
* V3-8-V4 V4-8-V5 V5-8-V6 V6-8-V7
*/
lifetimeGraph.addEdge(0, 1, 1);
lifetimeGraph.addEdge(0, 2, 2);
lifetimeGraph.addEdge(0, 3, 6);
lifetimeGraph.addEdge(0, 4, 1);
lifetimeGraph.addEdge(0, 5, 1);
lifetimeGraph.addEdge(0, 6, 1);
lifetimeGraph.addEdge(0, 7, 1);
lifetimeGraph.addEdge(1, 2, 8);
lifetimeGraph.addEdge(1, 7, 5);
lifetimeGraph.addEdge(2, 3, 8);
lifetimeGraph.addEdge(3, 4, 8);
lifetimeGraph.addEdge(4, 5, 8);
lifetimeGraph.addEdge(5, 6, 8);
lifetimeGraph.addEdge(6, 7, 8);
Edge[] edges = lifetimeGraph.lifetimePath(6, 4);
for (int i = 0; i < edges.length; i++) {
System.out.println(edges[i]);
}
}
}
三、程序分析
其实最后我同学告诉我理解错了题意,这个题不是求两点间的最长路径,而是求两点间生存时间最长的一条路径,lifetime不是距离,而是当前这条edge能够存在的时间。
但是其实非常好改进,只需要替换下面这段代码就行:改进的思路就是
一条路径的最大生存时间由该路径中lifetime最小的那条edge来决定
private Edge[] findMaxLifeTimePath(LinkedList> allPaths) {
Iterator> iterator = allPaths.iterator();
LinkedList max = null;
int maxLifeTime = 0;
while (iterator.hasNext()) {
int sum = -1 >>> 1;
// int sum = 0;
LinkedList next = iterator.next();
LinkedList next2 = new LinkedList<>();
next2.addAll(next);//不修改原有创建好的路径
//往下的代码很简单,就是计算出存活时间最长的路径
Integer pop = next.pop();
while(!next.isEmpty()) {
Integer pop1 = next.pop();
Vertex vertex = adjacencyList.get(pop);
Edge edgeTo = vertex.getEdgeTo(adjacencyList.get(pop1));
int lifetime = edgeTo.getLifetime();
sum = sum > lifetime ? lifetime : sum;//一条路径的最大生存时间由该路径中lifetime最小的那条edge来决定
pop = pop1;
}
if(sum >= maxLifeTime) {
if (sum > maxLifeTime || max.size() > next2.size()) {
maxLifeTime = sum;
max = next2;
}
}
}
自我感觉非常差劲,像老太太的裹脚布一样又臭又长,但是想了好久没有想到如何用栈来替代递归。
希望大家在评论区给出一些指导性的意见。