永磁同步电机的矢量控制策略（一）一一一坐标变换

1.永磁同步电机的矢量控制策略（一）

1.1 矢量控制策略的综述

1971年，德国西门子公司F.Blaschke等提出的“感应电机磁场定向的控制原理”和美国P.C.Custman与A.A.Clark申请的专利“感应电机定子电压的坐标变换控制”奠定了矢量控制的基础。多年来，经过学者和工程技术人员的不断完善改进，形成现有的矢量控制变频调速系统。

其主要特点是：通过矢量变换的方法重构电机数学模型为一台他励直流电动机，在同步旋转的参考轴系内，将交变的定子电流变换为两个直流量，一个为励磁（直轴 id）分量，一个为转矩（交轴 iq）分量，两者在空间上相互垂直，通过对两者进行解耦控制，以实现对电机励磁磁场和电磁转矩的解耦控制。

目前常用的矢量控制策略，根据电流控制方法主要分为：id=0控制、cosφ=1控制、最大转矩/电流控制（MTPA）、恒磁链控制等。其中每种方法都有各自的特点和适用场合，下面将从最基础的矢量控制一点点的进行讲解。我们知道，标准的FOC（矢量控制）是由电流环、转速环和PWM控制算法组成的。而它们得以实现的基础正是坐标变换。

1.2 为什么要进行坐标变换？

1.永磁同步电机中，定子磁势Fs、转子磁势Fr、气隙磁势之间的夹角都不是90°，耦合性强，根本无法对磁场和电磁转矩进行独立控制；2.直流电机励磁磁场垂直于电枢磁势，二者各自独立，互不影响；3.直流电机控制策略多种多样，能够使其应对不同场合。主要是将交流电机模拟成直流电机来进行控制。

1.3 矢量控制的坐标变换介绍

对于正弦波永磁同步电机，所有的矢量控制算法都是建立在电机的数学模型上。通过坐标变换，把三相交流绕组等效成旋转的两相相互垂直的直流绕组，变换后使得系统变量之间得到部分解耦，从而使系统的分析与控制得到大量简化。而且，PMSM的数学模型不仅可以用于分析正弦波永磁同步电机的稳态运行性能，还可以用于分析电机的瞬时性能。

图1 三种坐标系的空间位置关系

矢量控制系统中要用到的坐标系可分为两类：一类是静止坐标系，包括三相静止坐标系ABC和两相静止坐标系aβ；另一类是旋转坐标系，分为转子旋转坐标系、定子旋转坐标系，这里用到的是转子旋转坐标系dq。如图1所示。通常将ABC三相静止坐标系变换到两相静止坐标系aβ称作Clarke变换，而将aβ变换到两相旋转坐标系dq称作Park变换。以下具体说明两种坐标变换的具体过程。然而实际仿真中我们是直接将三相静止的自然坐标系直接变换到与转子同步旋转的坐标系中，称之为Park变换。从下面的仿真可看出坐标变换前后的结果。

1.3.1 Clarke变换

为了简化运算，定义两相静止坐标系中的a轴与定子A相绕组重合，β轴逆时针超前a轴90空间电角度。如图2和图3所示。根据恒幅值变换原则得到变换矩阵C3s/2s为：

根据上式可以将三相静止坐标系下的物理量变换到两相静止坐标系可表示为：

式中的 f 可以代表电压、电流和磁链。

图2 由三相静止坐标系变换为两相静止坐标系位置关系

图3 三相正弦波经Clarke变换后的理论变换结果

具体的推导手稿过程如图所示：

在交流调速系统中，有两种等效变换方式：一种是恒功率变换，因变换前后磁动势保持不变，所以变换后功率也不变；另一种是恒幅值变换，变换前后电压、电流的幅值不变，但dq旋转坐标系下的功率需要再乘以1.5才是电机实际的功率。本文所涉及到的坐标变换均采用第二种方法，即恒幅值变换。

小结：

对于变换公式的系数
若采用恒幅值变换，k = 3/2。
若采用恒功率变换，k = （2/3）^0.5

对于转矩公式的系数
若采用恒幅值变换，电磁转矩Te前面需要乘以系数3/2。
若采用恒功率变换，电磁转矩Te前需要乘系数1。

1.3.2 Park 变换

定义一个在空间以同步速旋转的两相坐标系 dq，其中 d 轴与转子磁极轴线重合，q 轴逆时针超前 d 轴 90° 空间电角度，d 轴与 A 相定子绕组的夹角为 θ 。如图4所示。同样可以得到变换矩阵 C 2s/2r 为：

可得到物理量在两相旋转坐标系下可表示为：

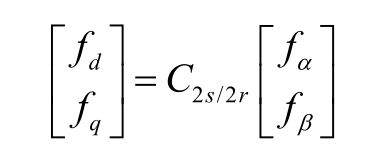
式中的 f 可以代表电压、电流和磁链。

图4 三种坐标系下的等效变换

具体的推导手稿过程如图所示：

如果将Clarke变换和Park 变换相结合，可得到三相静止系统中的物理量在 dq 轴系统中可表示为：

1.4 矢量控制的坐标变换仿真

1.4.1 Clarke变换的仿真

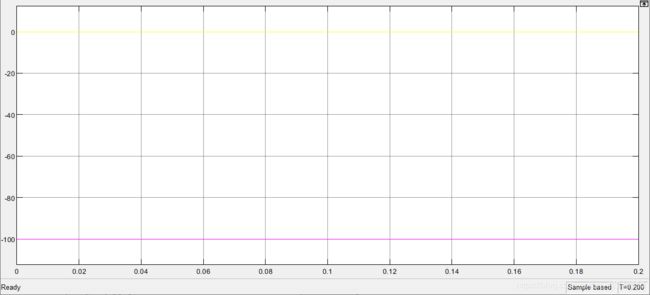
依据所推导的公式搭建Simulink仿真模型，如图4所示。仿真结果与理论结果相一致，如图5所示。

图4
输入的三相正弦交流信号


图5

1.4.2 Park 变换的仿真

依据所推导的公式搭建Simulink仿真模型，如图6所示。仿真结果与理论结果相一致，如图7所示。

图6

图7

小结：

1.运用坐标变换可以 将交流电机近似看成是直流电机的控制方式，为后续控制展开奠定基础。
其中对于变换矩阵的系数确定有：
对于变换公式的系数
若采用恒幅值变换，k = 3/2。
若采用恒功率变换，k = （2/3）^0.5

对于转矩公式的系数
若采用恒幅值变换，电磁转矩Te前面需要乘以系数3/2。
若采用恒功率变换，电磁转矩Te前需要乘系数1。

2.将三相交流的信号经过Clarke变换转变为两相正弦波信号，再经过Park变换转变为仅有一相相电流。