初始化 | VINS-Mono 论文公式推导与代码解析分讲

2. 初始化(松耦合)
   在提取的图像的Features和做完IMU的预积分之后，进入了系统的初始化环节，主要的目的有以下两个：
   系统使用单目相机，如果没有一个良好的尺度估计，就无法对两个传感器做进一步的融合，这个时候需要恢复出尺度；
   要对IMU进行初始化，IMU会受到bias的影响，所以要得到IMU的bias。

所以我们要从初始化中恢复出尺度、重力、速度以及IMU的bias，因为视觉(SFM)在初始化的过程中有着较好的表现，所以在初始化的过程中主要以SFM为主，然后将IMU的预积分结果与其对齐，即可得到较好的初始化结果。

2.1 相机与IMU之间的相对旋转相机与IMU之间的旋转标定非常重要，偏差1-2°系统的精度就会变的极低。设相机利用对极关系得到的旋转矩阵为 ，IMU经过预积分得到的旋转矩阵为 ，相机与IMU之间的相对旋转为 ，则对于任一帧满足

将旋转矩阵写为四元数，则上式可以写为

将其写为左乘和右乘的形式


那么对于 对测量值，则有

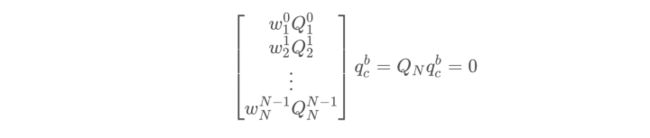
其中 为外点剔除权重，其与相对旋转求得的角度残差有关， 为计算相对旋转需要的测量对数，其由最终的终止条件决定。角度残差可以写为，

至此，就可以通过求解方程 得到相对旋转，解为 的左奇异向量中最小奇异值对应的特征向量。但是，在这里还要注意求解的终止条件(校准完成的终止条件)。在足够多的旋转运动中，我们可以很好的估计出相对旋转 ,这时 对应一个准确解，且其零空间的秩为1。但是在校准的过程中，某些轴向上可能存在退化运动(如匀速运动)，这时 的零空间的秩会大于1。判断条件就是 的第二小的奇异值是否大于某个阈值，若大于则其零空间的秩为1，反之秩大于1，相对旋转) 的精度不够，校准不成功。

对应代码在InitialEXRotation::CalibrationExRotation中。
// 相机与IMU之间的相对旋转
if(ESTIMATE_EXTRINSIC == 2)
{
ROS_INFO(“calibrating extrinsic param, rotation movement is needed”);
if (frame_count != 0)
{
// 选取两帧之间共有的Features
vector> corres = f_manager.getCorresponding(frame_count - 1, frame_count);

    // 校准相机与IMU之间的旋转
    Matrix3d calib_ric;
    if (initial_ex_rotation.CalibrationExRotation(corres, pre_integrations[frame_count]->delta_q, calib_ric))
    {
        ROS_WARN("initial extrinsic rotation calib success");
        ROS_WARN_STREAM("initial extrinsic rotation: " << endl << calib_ric);
        ric[0] = calib_ric;
        RIC[0] = calib_ric;
        ESTIMATE_EXTRINSIC = 1;
    }
}

}

2.2 检测IMU可观性// 计算均值
map::iterator frame_it;
Vector3d sum_g;
for (frame_it = all_image_frame.begin(), frame_it++; frame_it != all_image_frame.end(); frame_it++)
{
double sum_dt = frame_it->second.pre_integration->sum_dt;
Vector3d tmp_g = frame_it->second.pre_integration->delta_v / sum_dt;
sum_g += tmp_g;
}
Vector3d aver_g = sum_g * 1.0 / ((int)all_image_frame.size() - 1);

// 计算方差
double var = 0;
for (frame_it = all_image_frame.begin(), frame_it++; frame_it != all_image_frame.end(); frame_it++)
{
double sum_dt = frame_it->second.pre_integration->sum_dt;
Vector3d tmp_g = frame_it->second.pre_integration->delta_v / sum_dt;
var += (tmp_g - aver_g).transpose() * (tmp_g - aver_g);
}

// 计算标准差
var = sqrt(var / ((int)all_image_frame.size() - 1));
//ROS_WARN(“IMU variation %f!”, var);
if(var < 0.25) //! 以标准差判断可观性
{
ROS_INFO(“IMU excitation not enouth!”);
//return false;
}

2.3 相机初始化（Vision-Only SFM）求取本质矩阵求解位姿
三角化特征点
PnP求解位姿
转换到IMU坐标系下
坐标系作为参考系
不断重复直到恢复出滑窗内的Features和相机位姿

2.4 视觉与IMU对齐
Gyroscope Bias Calibration
Velocity, Gravity Vector and Metric Scale Initialization
Gravity Refinement
Completing Initialization

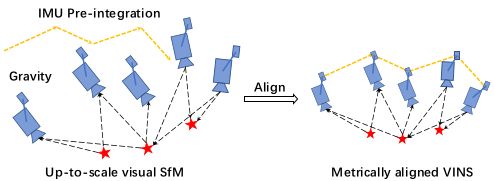
对应代码：VisualIMUAlignment陀螺仪Bias标定

求解上式的最小二乘解，即可得到 ,注意这个地方得到的只是Bias的变化量，需要在滑窗内累加得到Bias的准确值。
对应代码：solveGyroscopeBias

void solveGyroscopeBias(map &all_image_frame, Vector3d* Bgs) {
Matrix3d A;
Vector3d b;
A.setZero();
b.setZero();

map::iterator frame_i;
map::iterator frame_j;
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++) {
    frame_j = next(frame_i);

    MatrixXd tmp_A(3, 3);
    VectorXd tmp_b(3);
    tmp_A.setZero();
    tmp_b.setZero();

    Eigen::Quaterniond q_ij(frame_i->second.R.transpose() * frame_j->second.R);
    tmp_A = frame_j->second.pre_integration->jacobian.template block<3, 3>(O_R, O_BG);
    tmp_b = 2 * (frame_j->second.pre_integration->delta_q.inverse() * q_ij).vec();

    A += tmp_A.transpose() * tmp_A;
    b += tmp_A.transpose() * tmp_b;
}

Vector3d delta_bg = A.ldlt().solve(b);
ROS_WARN_STREAM("gyroscope bias initial calibration " << delta_bg.transpose());

// 因为求解出的Bias是变化量，所以要累加
for (int i = 0; i <= WINDOW_SIZE; i++)
    Bgs[i] += delta_bg;

// 利用新的Bias重新repropagate
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++) {
    frame_j = next(frame_i);
    frame_j->second.pre_integration->repropagate(Vector3d::Zero(), Bgs[0]);
}

}
初始化速度、重力向量和尺度因子

通过Cholosky分解求解
对应代码：LinearAlignment
优化重力

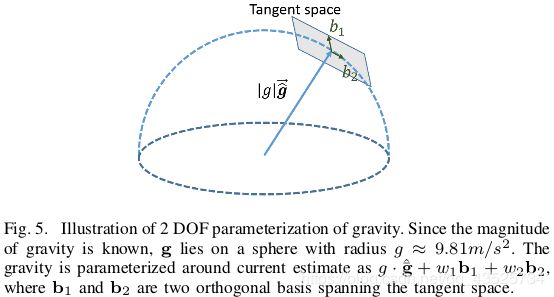
重力矢量的模长固定（9.8），其为2个自由度，在切空间上对其参数化

同样，通过Cholosky分解求得 ，即相机 系下的重力向量。
最后，通过将 旋转至惯性坐标系（世界系）中的 z 轴方向[0,0,1]，可以计算第一帧相机系到惯性系的旋转矩阵 ，这样就可以将所有变量调整至惯性世界系（水平坐标系，z轴与重力方向对齐）中。
对应代码：RefineGravity