算法之深搜与广搜

在经过8次算法课的学习后，自己的能力提升了很多，只不过对于学的知识很多都不是很懂，懂的中也有一些很不熟练，先将自己较为熟练的深搜与广搜做一个整理；

深度优先搜索（Depth-First-Search）其概念简要的说就是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次.该算法用到的事递归思想；递归需要两个部分：基线条件和递归条件；

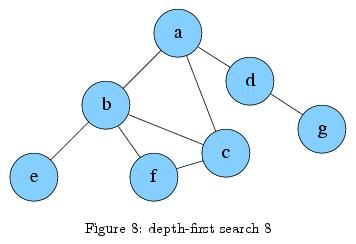
我们从a出发，先到b,再到e,之后回去，到b,再到c,c再回到f,f再回到b,b再回到a,再从a到d,再从d到g,再从g回到d，再从d回到a,发现所有节点都已经遍历，深度搜索结束；

总的来说，深度优先搜索，就是一条路走到底的策略，直到再也不能走为止，这种思想正是可以用递归实现的，因此用深度优先搜索，设立一个停止条件（即没有搜索的东西），然后一次一次的向下递归，直到遍历了所有的节点

void dfs()//参数用来表示状态  
{  
    进行一些操作，由题目决定
    if(到达终点状态)  
    { 
        return;  
    }  
    if(不符合题意)  
        return;  
    if(符合题意)  
     {  
        修改操作;
        dfs（）；  
       }    
}  

dfs的题目分为两大类，第一类时在图上进行深搜，图可以选择邻接矩阵进行存储（也可以用vector或者前向星来存储，邻接矩阵比较简单，但是如果点过多的话，就不适用了)，之后再进行遍历，接下来有几道基础题:

B - Counting Sheep HDU-2952
连通块类的问题，从起点开始上下左右四个方向进行搜索，搜索到的都标记为无羊，表示自己已经搜索过这里，当完全搜不到时，计数器便自加，在搜索下一个有羊的区域，同样还有八个方向的搜索的题目，同理。

代码：

#include
#include
using namespace std;
int dx[4]={0,-1,0,1},dy[4]={-1,0,1,0};//定义搜索方向
int n,row,line,number;
char a[105][105];//存储图的数组
void dfs(int i,int j){
    a[i][j]='.';
    for(int q=0;q<4;q++){
        int nx=i+dx[q],ny=j+dy[q];
        if(nx>=0&&nx=0&&ny>n;
    for(int i=0;i>row>>line;
        for(int j=0;j>a[j];
        for(int i=0;i

A - 棋盘问题 POJ-1321
此题与n皇后问题很像，即放一棵棋子，之后对所有放置其他棋子的方式，进行搜索，直到找到，计数器自加，其中要保证行和列不能有两枚棋子；

代码：

#include
#include
#include
using namespace std;
char a[10][10];//记录棋盘位置
int book[10]={0};
int n,k,cnt,m;
void dfs(int cur)
{
    if(k==m)//终点状态
    {
        cnt++;
        return ;
    }
    if(cur>=n)//不符合题意
        return ;
    for(int j=0; j

第二类数据类

这类题本人也没怎么做过，直接放题：
HDU 1015-Safecraker(回溯，字符处理)

接下来时bfs：
bfs也是运用递归的思想，不过其运用了队列的数据结构，队列的特性是，先进先出，与栈的先进后出是不同的，废话不多说，放张关于队列的图：

详细用法:
定义一个queue的变量 queue M
查看是否为空范例 M.empty() 是的话返回1，不是返回0;
从已有元素后面增加元素 M.push()
输出现有元素的个数 M.size()
显示第一个元素 M.front()
显示最后一个元素 M.back()
清除第一个元素 M.pop()
（需要加上queue的头文件声明)

bfs也就是利用队列先进先出的性质，对图进行一层一层的搜索，直到找到元素为止，bfs多用于求图上的到达某点的最短路径（做题甚少，只知道这种题型），即多用于迷宫问题。
例题：
给定一个大小为N*M的迷宫，由通道(’.’)和墙壁(’#’)组成，其中通道S表示起点，通道G表示终点，每一步移动可以达到上下左右中不是墙壁的位置。试求出起点到终点的最小步数。（本题假定迷宫是有解的）(N,M<=100)
样例输入：10 10

样例输出：22

代码：

#include
#include
#include
#include
#include
#include
#include
using namespace std;
 int m,n;
const int INF =100000000;
typedef pair P;
char maze[200][200];
int sx,sy;
int gx,gy;
int d[200][200];
void panduan(int m,int n)
{
    for(int i=0;i que;
    for(int i=0;i

F - 非常可乐 HDU-1495

这个题，一共有六种动作，瓶倒杯1，杯1到瓶，瓶到杯2，杯2到瓶，杯一到杯2，杯2到杯1。6种动作是平行的，属于同一级别，之后对每种动作进行搜索，停止条件为有两个容器中有相同的可乐，用一个东西计算搜索的次数，即为答案。

#include
#include
#include
#include
using namespace std;
int s[3];
int book[105][105][105];标记某种状态是否走过
int half;
struct cup
{
    int c[3];
    int a;
}p,temp;
void init()
{
    for(int i=0;i<105;i++)
        for(int j=0;j<105;j++)
            for(int k=0;k<105;k++)
                book[i][j][k]=0;
    book[s[0]][s[1]][s[2]]=1;//最初始状态
}
void bfs()
{
    queue  q;
    p.c[0]=s[0];
    p.c[1]=0;
    p.c[2]=0;
    p.a=0;
    q.push(p);//把初始状态压入队列中
    while(q.empty()==0)
    {
        p=q.front();
        q.pop();
        for(int i=0;i<3;i++)
        {
            if(p.c[i]>0)
            {
                for(int j=0;j<3;j++)
                {
                    temp=p;
                    if(i==j)
                        continue;
                    if(temp.c[i]>s[j]-temp.c[j])//可以倒水，且倒满了
                    {
                        temp.c[i]-=s[j]-temp.c[j];
                        temp.c[j]=s[j];
                    }
                    else{                               //倒不满
                        temp.c[j]+=temp.c[i];
                        temp.c[i]=0;
                    }
                    if(book[temp.c[0]][temp.c[1]][temp.c[2]]==0)
                    {
                        book[temp.c[0]][temp.c[1]][temp.c[2]]=1;
                        temp.a++;
                        int d=0;
                        for(int k=0;k<3;k++)
                        {
                            if(temp.c[k]==half)
                                d++;
                        }
                        if(d==2)
                        {
                            cout<>s[i];
    }
    if(s[0]==0&&s[1]==0&&s[2]==0)
        break;
    init();
    if(s[0]%2)
        cout<<"NO"<

搜索的优化:

1. 记忆化搜索：
   所谓记忆化搜索就是，在每次状态转移的时候，判断一下这个状态是否已经转移过了，如果转移过了，直接调用他的结果就好了，这可以减小搜索的时间复杂度，并且避免了向栈中压入过多的数据，导致爆栈的错误（不过本人表示从未遇到爆栈的错误。）
   例题：
   洛谷 p3953
   洛谷自带题解！！！

2. 剪枝：
   剪枝也就是将一些不符合规则的树枝剪掉，来减小时间复杂度
   例题:
   POJ 1011
   附带详细题解

3. 双向搜索:
   所谓双向搜索，就是从上往下，从下往上一块搜索，之后再“合并数据”，由于自己也不懂，所以附上一篇博文来解释
   双向搜索博客

4. 迭代加深
   所谓迭代加深，就是设定一定的层数限制，然后进行搜索，如果搜不到，则加深层数，直到最后一层为止，这样避免了所要找的结果在很低的层数却花了很长的时间去找

例如上图这种情况，如果照常规方法去搜索，那么需要遍历所有节点才能找到，但是如果采用迭代加深的方法，设定一定的层数限制，就可以很快找到。

自己了解的搜索算法，到这里就没了，没发过什么博文，如果有错误和不当的地方，敬请指正。