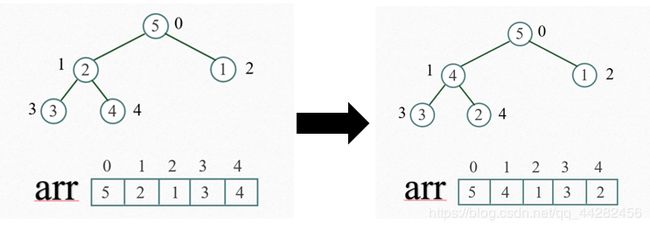
堆排序中每次堆调整后的次序
堆排序中每次堆调整后的次序
未经允许,不得转载!
引言
堆排序是对简单选择排序的一种改进,改进的着眼点是如何减少选择的比较次数。在特定的条件下,堆排序的效率是明显优于快速排序的。那么,堆排序是如何减少记录的比较次数,提高整个排序的效率的?
需求分析
问题描述
堆排序(heap sort)是对简单选择排序的一种改进,改进的着眼点是:如何减少记录的比较次数。简单选择排序在一趟排序中仅选出最小记录,没有把一趟的比较结果保存下来,因而记录的比较次数较多。堆排序在选出最小记录的同时,也找出较小记录,减少了选择的比较次数,从而提高整个排序的效率。堆排序算法的基本思想如下:
首先将待排序序列构造成一个大根堆,即选出了堆中所有记录的最大者,将它从堆中移走,并将剩余的记录再调整成堆,这样又找出了次小的记录,以此类推,直到堆中只有一个记录。
现在希望算出从小到大堆排序的过程中,每次进行堆调整后(包括构造初始堆),打印输出堆的次序。

【输入形式】
第一行一个整数N, 第二行有N个整数,无序。0
输出共 N 行。第i行对应第i次堆调整后N-i+1个整数的次序。
问题分析
该问题涉及的数据结构中的排序问题,排序技术有插入排序、交换排序、选择排序、归并排序、分配排序五种方式,本题正是选择排序中的堆排序算法。通过构造初始堆,将给定无序序列构造成一个大根堆,再将堆顶元素与末尾元素进行交换,使堆顶元素最大,末尾元素最小。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换,从而得到每次堆调整的次序,所以这是一个如何实现堆排序的问题。
总体设计
在进行堆排序之前,首先要了解堆的定义,同时考虑到堆的非线性结构,所以在这里以数组存储,堆顶元素下标以0开始计算,若父节点的下下标为i,则父节点的左孩子结点下标为2i+1,右孩子结点下标为2i+2。然后通过问题描述中堆排序的基本思想,构建一个堆,考虑到具体问题,在这里构建大根堆,再进行对调整,利用重复构建大根堆的方法,把最大的放到根节点,然后把根节点与最后一个节点交换数值进行排序。通过输出函数,输出每次堆调整后堆(包括构造的初始堆)的次序。
堆的定义
堆是一种非线性结构,可以把堆看作一个数组,也可以被看作一个完全二叉树,通俗来讲堆其实就是利用完全二叉树的结构来维护的一维数组。按照堆的特点可以把堆分为大根堆和小根堆:
大根堆:每个结点的值都大于或等于其左右孩子结点的值;
小根堆:每个结点的值都小于或等于其左右孩子结点的值。
在本题中主要运用大根堆进行具体的堆排序。
堆的特点
大根堆的特点
(1)根节点(即为堆顶)的值是所有结点中的最大值;
(2)对于任意一个子节点来说,均不大于其父节点的值,必须要注意一点,只要求子节点与父节点的关系,两个节点的大小关系与其左右位置没有任何关系;
(3)较大值得结点靠近根结点,但不是绝对的。
层序编号的特点
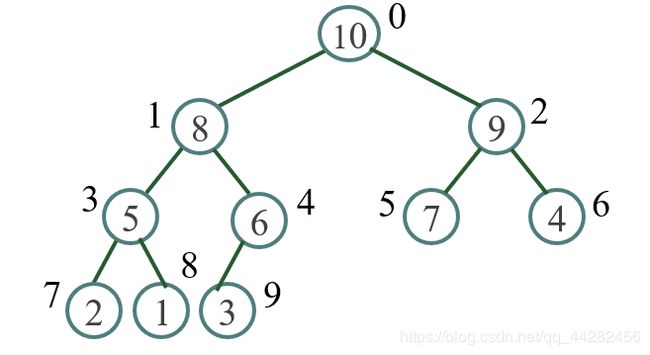
通过对图2.1大根堆示例进行层序编号,设编号为k(0,1,2…),已知元素编号为i,父结点编号为(i-1)/2,左孩子结点编号为2i+1,右孩子结点为2i+2,可以得到如下特点:
ki>k2i+1;ki>k2i+2
堆排序的基本思想
首先将待排序序列构造成一个大根堆,即选出了堆中所有记录的最大者,将它从堆中移走,并将剩余的记录再调整成堆,这样又找出了次小的记录,以此类推,直到堆中只有一个记录。
①首先将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端。
②将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1。
③将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组。
堆的存储
考虑到堆的非线性结构和堆排序的基本思想,通过使用顺序存储结构的一维数组对堆进行存储,上面图2.1的大根堆结构映射成数组如下,

将上述数组定义为arr[ ],可以看到大根堆满足堆的定义性质,
arr(i)>arr(2i+1) && arr(i)>arr(2i+2)
构建初始堆
将给定无序序列构造成一个大顶堆,假设给定无序序列结构如下,
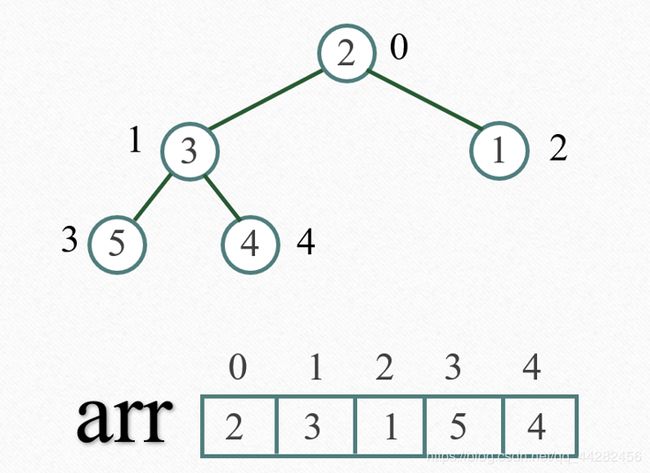
此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的3结点),从左至右,从下至上进行调整。
此处必须注意,我们把3和5比较交换之后,必须考虑5这个节点对于其子节点会不会产生任何影响?因为其是叶子节点,所以不加考虑;但是,一定要熟练这种思维,写代码的时候就比较容易理解为什么会出现一次非常重要的交换了。
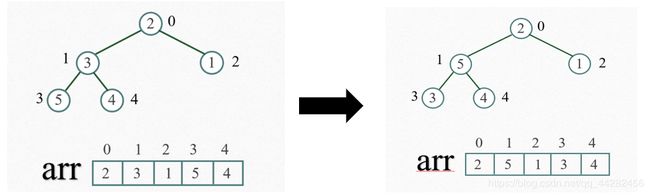
找到第二个非叶节点2,由于[2,5,1]中5元素最大,2和5交换。2和5交换过后,必须考虑5所在的这个节点位置,因为其上的值变了,必须判断对其的两个子节点是否还满足大根堆的原则,每一次交换,都必须要循环把子树部分判别清楚。
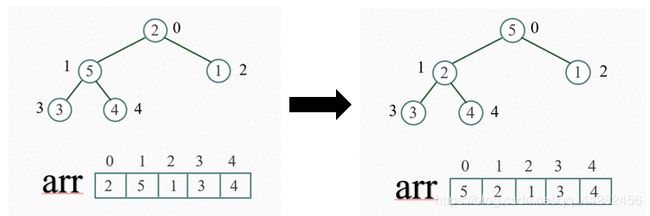
这时,交换导致了子树[2,3,4]结构混乱,继续调整,[2,3,4]中4最大,交换2和4。根据上面说的规则,每次交换都要把改变了的那个节点所在的树重新判定一下,2和4交换了,变动了的那棵子树就必须重新调整,一直调整到符合大根堆的规则为止。
固定最大值再构造堆

将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
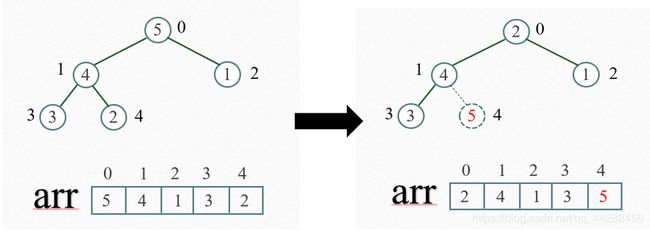
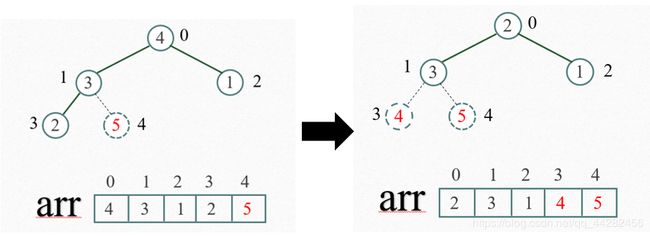
重新调整结构,使其继续满足堆定义。
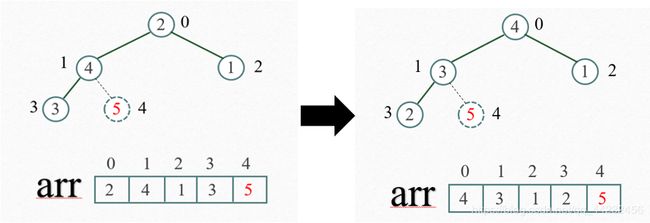
再将堆顶元素4与末尾元素2进行交换,得到第二大元素4。
重新调整结构,使其继续满足堆定义。
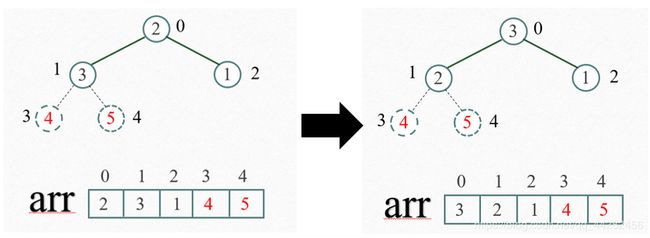
再将堆顶元素3与末尾元素1进行交换,得到第三大元素3。
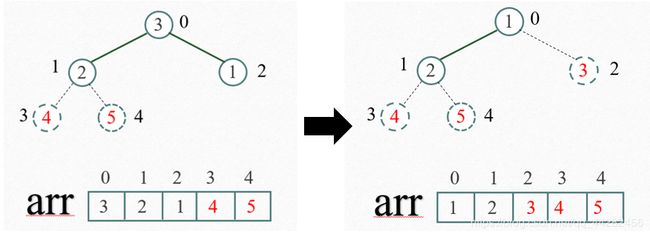
最后一次调整。
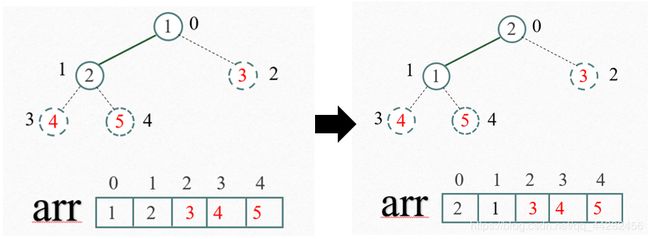
再将堆顶元素2与末尾元素1进行交换,得到第四大元素2。
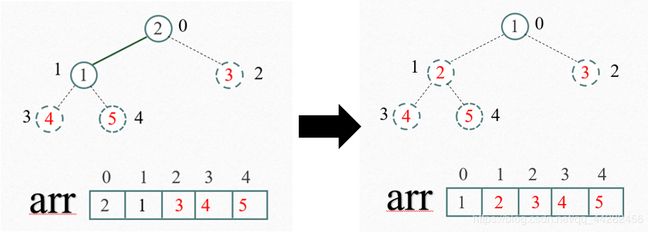
由此,得到最小元素1,堆调整结束。
详细设计
函数清单
代码清单
#include 程序运行结果测试与分析
示例数据 1
【输入数据】
5
2 3 1 5 4
【输出数据】
5 4 1 3 2
4 3 1 2
3 2 1
2 1
1
示例数据 2
【输入数据】
6
7 9 4 6 8 1
【输出数据】
9 8 4 6 7 1
8 7 4 6 1
7 6 4 1
6 1 4
4 1
1
示例数据 3
【输入数据】
6
28 36 32 25 18 16
【输出数据】
36 28 32 25 18 16
32 28 16 25 18
28 25 16 18
25 18 16
18 16
16
示例数据 4
【输入数据】
12
16 8 9 13 5 19 4 36 1 21 40 2
【输出数据】
40 36 19 16 21 9 4 13 1 8 5 2
36 21 19 16 8 9 4 13 1 2 5
21 16 19 13 8 9 4 5 1 2
19 16 9 13 8 2 4 5 1
16 13 9 5 8 2 4 1
13 8 9 5 1 2 4
9 8 4 5 1 2
8 5 4 2 1
5 2 4 1
4 2 1
2 1
1
结论与心得
在题目的求解过程中遇到诸多的问题和一定的错误,但是本着实事求是、求知探索的精神与态度,通过查询网络、查阅书籍、沟通交流等有效方式,解决了这些问题和错误,并在此过程中受益颇多。
首先,在构建大根堆时,对堆中的结点按层次进行编号的数组出现错误,数组从下标1开始,导致后续的函数运行错误,无法输出正确的结果,经过查询,发现本意思路应该是下标从0开始。
其次,在堆调整时通过固定最大值和在构造大根堆的方式进行堆排序,没有考虑到堆顶元素与末尾元素交换后的父结点对其左右孩子结点的影响,只顾将两元素进行交换,通过查阅资料和询问同学,发现了问题所在,并加以改进,调整函数。
最后,不论是本题还是数据结构课程设计这门课程,通过这段时间的学习与练习,我对数据结构的基本知识有了更深层次的理解。同时,对算法和程序设计有了全新的看法。堆排序问题只是数据结构中的基本问题,希望在日后的程序设计和软件开发过程中,能够保持如今的态度实事求是,务实笃行。