总结
A. 不知道叫什么名字
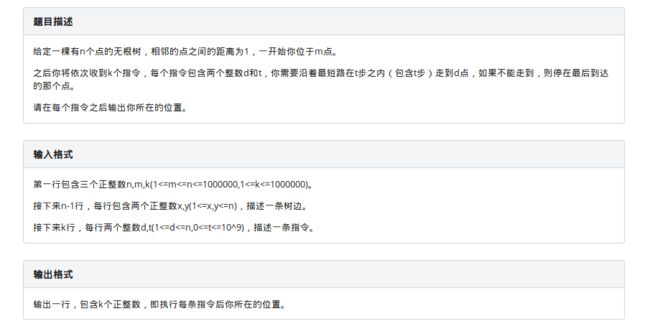
题目描述
分析
一道裸的LCA板子题,就是卡常有点难受,注释在代码里
代码
#include
using namespace std;
const int maxn=22,maxk=1000005;
int f[maxk][maxn];
int head[maxk],tot=1;
struct asd{
int to,next,val;
}b[maxk>>1];
inline int read(){
int s=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
s=s*10+ch-'0';
ch=getchar();
}
return s*f;
}
inline void write(int x){
if(x<0){
putchar('-');
x=-x;
}
if(x>9)
write(x/10);
putchar(x%10+'0');
}
void ad(int aa,int bb,int cc){
b[tot].to=bb;
b[tot].next=head[aa];
b[tot].val=cc;
head[aa]=tot++;
}
int dep[maxk];
void dfs(int now,int fa,int da){
f[now][0]=fa;
dep[now]=dep[fa]+1;
for(int i=1;(1<>=1;
k++;
}
if(xx==yy) return xx;
for(int i=20;i>=0;i--){
if(f[xx][i]==f[yy][i]) continue;
xx=f[xx][i];
yy=f[yy][i];
}
return f[xx][0];
}
int main(){
memset(head,-1,sizeof(head));
int n,m,k;
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i=bb){//如果当前节点到公共祖先的距离大于步数
int ans=bb;
int k=0;
while(ans){
if(ans&1) bef=f[bef][k];
k++;
ans>>=1;
}
write(bef);//将之前的节点想上跳要到达的步数
printf(" ");
} else {//如果当前节点到公共祖先的距离小于步数,则在另一分支
int ans=bb-now;//求出在另一分支上的步数
int zjz=dep[aa]-dep[gg];//求出要到达的节点到最近公共祖先的距离
int zjz2=zjz-ans;//距离减去步数
int k=0;
while(zjz2){
if(zjz2&1) aa=f[aa][k];
k++;
zjz2>>=1;
}
write(aa);
printf(" ");
bef=aa;
}
}
}
return 0;
}
B、虫洞
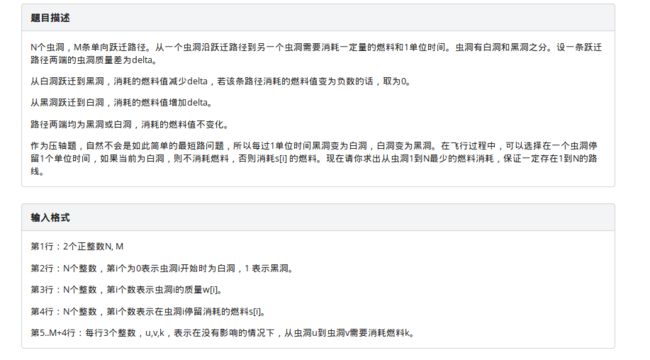
题目描述
分析
我们建两层点,其中\([1,n]\)代表白洞,\([n+1,n\times 2]\)代表黑洞
如果我们建边的时候,如果该边上的两个点都是黑洞或者白洞
那么在我们进行跃进的时候,只需要花费原来的价值就可以
所以我们从\(aa\)到\(bb+n\),从\(aa+n\)到\(bb\)分别建一条边,权值为输入的权值即可
如果两个点一个是黑洞一个是白洞,我们就按照题目中的要求建边
最后我们还要考虑在某个节点停留的情况
我们需要从\(i\)到\(i+n\)建一条权值为\(0\)的边,代表在白洞停留
从\(i+n\)到\(i\)建一条权值为该点燃料消耗的边,代表在黑洞停留
代码
#include
using namespace std;
const int maxn=6e5+5;
typedef long long ll;
struct asd{
int from,to,next;
ll val;
}b[maxn];
int head[maxn],tot=1;
void ad(int aa,int bb,ll cc){
b[tot].from=aa;
b[tot].to=bb;
b[tot].val=cc;
b[tot].next=head[aa];
head[aa]=tot++;
}
int hd[maxn];
ll zl[maxn],rl[maxn];
struct jie{
int num,tim,kk;
ll jl;
jie(int aa=0,ll bb=0){
num=aa,jl=bb;
}
bool operator < (const jie& A)const {
return jl>A.jl;
}
};
priority_queue q;
ll dis[maxn];
bool vis[maxn];
void dij(int xx){
memset(dis,0x3f,sizeof(dis));
dis[xx]=0;
q.push(jie(xx,0));
while(!q.empty()){
int now=q.top().num;
q.pop();
if(vis[now]) continue;
vis[now]=1;
for(int i=head[now];i!=-1;i=b[i].next){
int u=b[i].to;
if(dis[u]>dis[now]+b[i].val){
dis[u]=dis[now]+b[i].val;
q.push(jie(u,dis[u]));
}
}
}
}
int main(){
memset(head,-1,sizeof(head));
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&hd[i]);
}
for(int i=1;i<=n;i++){
scanf("%lld",&zl[i]);
}
for(int i=1;i<=n;i++){
scanf("%lld",&rl[i]);
}
for(int i=1;i<=m;i++){
int aa,bb;
ll cc;
scanf("%d%d%lld",&aa,&bb,&cc);
if(hd[aa]==hd[bb]){
ad(aa,bb+n,cc);
ad(aa+n,bb,cc);
} else {
ll cz=abs(zl[aa]-zl[bb]);
ad(aa+n,bb+n,cc+cz);
ad(aa,bb,max(cc-cz,0ll));
}
}
for(int i=1;i<=n;i++){
ad(i,i+n,0ll);
ad(i+n,i,rl[i]);
}
if(hd[1]==1) dij(n+1);
else dij(1);
printf("%lld\n",min(dis[n],dis[n*2]));
return 0;
}
C、图腾计数
题目描述
分析
我们将所有的元素从小到大排一下序,用线段树维护该元素的两边有多少元素比它小
再将所有的元素从大到小排一下序,用线段树维护该元素的两边有多少元素比它大
最后统计答案即可
代码
#include
using namespace std;
const int maxn=200005;
typedef long long ll;
struct asd{
int wz;
ll qz;
}b[maxn];
ll sumlmin[maxn],sumrmin[maxn],sumlmax[maxn],sumrmax[maxn];
bool cmpmin(asd aa,asd bb){
return aa.qzbb.qz;
}
bool cmp(asd aa,asd bb){
return aa.wz>1;
build(da<<1,l,mids);
build(da<<1|1,mids+1,r);
push_up(da);
}
void xgmin(int da,int t,ll w){
if(tr[da].l==tr[da].r){
tr[da].mmin+=w;
return;
}
int mids=(tr[da].l+tr[da].r)>>1;
if(t<=mids) xgmin(da<<1,t,w);
else xgmin(da<<1|1,t,w);
push_up(da);
}
void xgmax(int da,int t,ll w){
if(tr[da].l==tr[da].r){
tr[da].mmax+=w;
return;
}
int mids=(tr[da].l+tr[da].r)>>1;
if(t<=mids) xgmax(da<<1,t,w);
else xgmax(da<<1|1,t,w);
push_up(da);
}
ll cxmin(int da,int l,int r){
if(tr[da].l>=l && tr[da].r<=r){
return tr[da].mmin;
}
int mids=(tr[da].l+tr[da].r)>>1;
ll ans=0;
if(l<=mids) ans+=cxmin(da<<1,l,r);
if(r>mids) ans+=cxmin(da<<1|1,l,r);
return ans;
}
ll cxmax(int da,int l,int r){
if(tr[da].l>=l && tr[da].r<=r){
return tr[da].mmax;
}
int mids=(tr[da].l+tr[da].r)>>1;
ll ans=0;
if(l<=mids) ans+=cxmax(da<<1,l,r);
if(r>mids) ans+=cxmax(da<<1|1,l,r);
return ans;
}
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lld",&b[i].qz);
b[i].wz=i;
}
build(1,1,n);
sort(b+1,b+1+n,cmpmin);
for(int i=1;i<=n;i++){
sumlmin[b[i].wz]=cxmin(1,1,b[i].wz);
sumrmin[b[i].wz]=cxmin(1,b[i].wz,n);
xgmin(1,b[i].wz,1);
}
sort(b+1,b+1+n,cmpmax);
for(int i=1;i<=n;i++){
sumlmax[b[i].wz]=cxmax(1,1,b[i].wz);
sumrmax[b[i].wz]=cxmax(1,b[i].wz,n);
xgmax(1,b[i].wz,1);
}
sort(b+1,b+1+n,cmp);
ll ansmin=0,ansmax=0;
for(int i=1;i<=n;i++){
ansmin+=sumlmin[i]*sumrmin[i];
ansmax+=sumlmax[i]*sumrmax[i];
}
printf("%lld %lld\n",ansmax,ansmin);
return 0;
}
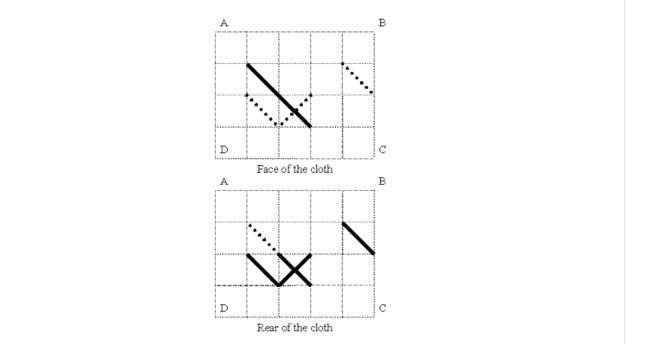
D、十字绣
题目描述
分析
一开始以为是一道DP题,后来发现状态不太好转移
后来看了题解才发现竟然是一道图论+\(dfs\),确实不太好想
我们把格子上的点抽象成图中的节点,同时开一个数组记录它的入度
如果该点与正面的某一条线相连,我们就把它的入度加\(1\)
如果该点与反面的某一条线相连,我们就把它的入度减\(1\)
那么这一个点所需要的线的数量就是它的入度的绝对值
我们来举一个例子,如果一个点连着\(3\)个正面的线,又连着\(2\)个反面的线
那么\(2\)个正面的线就会和\(2\)个反面的线抵消,也就是转了一圈
而剩下的那一个正面的线必须另用一针
这样,对于每一个联通块,我们统计该联通块内所有节点的入度之和,最后把它除以二
因为一条线的起点和终点我们分别算了一遍
有一种特殊情况就是该联通块所有节点的入度之和为\(0\)
这说明一条线就可以解决,要特判一下
最后要注意字符''在判断的时候要写成'\',或者用它的\(ASCII\)值\(92\),否则会报错
代码
#include
using namespace std;
const int maxn=1e6+5,maxk=205;
int head[maxn],tot=1,du[maxn],cnt,a[maxk][maxk],bb[maxn],ans,vis[maxn];
struct asd{
int from,to,next;
}b[maxn];
void ad(int aa,int bb,int cc){
b[tot].from=aa;
b[tot].to=bb;
b[tot].next=head[aa];
head[aa]=tot++;
if(cc==0) du[aa]++;
else du[aa]--;
}
char s[maxk][maxk];
void dfs(int now){
ans+=abs(du[now]);
vis[now]=1;
for(int i=head[now];i!=-1;i=b[i].next){
int u=b[i].to;
if(vis[u]==0){
dfs(u);
}
}
}
int main(){
memset(head,-1,sizeof(head));
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n+2;i++){
for(int j=1;j<=m+2;j++){
a[i][j]=++cnt;
}
}
for(int i=1;i<=n;i++){
scanf("%s",s[i]+1);
for(int j=1;j<=m;j++){
if(s[i][j]=='\\'){
ad(a[i][j],a[i+1][j+1],0);
ad(a[i+1][j+1],a[i][j],0);
bb[a[i][j]]=bb[a[i+1][j+1]]=1;
}
if(s[i][j]=='/'){
ad(a[i][j+1],a[i+1][j],0);
ad(a[i+1][j],a[i][j+1],0);
bb[a[i][j+1]]=bb[a[i+1][j]]=1;
}
if(s[i][j]=='X'){
ad(a[i][j+1],a[i+1][j],0);
ad(a[i][j],a[i+1][j+1],0);
ad(a[i+1][j],a[i][j+1],0);
ad(a[i+1][j+1],a[i][j],0);
bb[a[i][j]]=bb[a[i+1][j]]=bb[a[i+1][j+1]]=bb[a[i][j+1]]=1;
}
}
}
for(int i=1;i<=n;i++){
scanf("%s",s[i]+1);
for(int j=1;j<=m;j++){
if(s[i][j]=='\\'){
ad(a[i][j],a[i+1][j+1],1);
ad(a[i+1][j+1],a[i][j],1);
bb[a[i][j]]=bb[a[i+1][j+1]]=1;
}
if(s[i][j]=='/'){
ad(a[i][j+1],a[i+1][j],1);
ad(a[i+1][j],a[i][j+1],1);
bb[a[i][j+1]]=bb[a[i+1][j]]=1;
}
if(s[i][j]=='X'){
ad(a[i][j+1],a[i+1][j],1);
ad(a[i][j],a[i+1][j+1],1);
ad(a[i+1][j],a[i][j+1],1);
ad(a[i+1][j+1],a[i][j],1);
bb[a[i][j]]=bb[a[i+1][j]]=bb[a[i+1][j+1]]=bb[a[i][j+1]]=1;
}
}
}
int mans=0;
for(int i=1;i<=cnt;i++){
if(bb[i] && !vis[i]){
ans=0;
dfs(i);
if(ans==0) mans+=2;
else mans+=ans;
}
}
printf("%d\n",mans/2);
return 0;
}