机器学习:信息熵理解
如果说概率是对事件确定性的度量、那么信息(包括信息量和信息熵)就是对事物不确定性的度量。信息熵是由香农(C.E.Shannon)在1948年发表的论文《通信的数据理论(A Mathematical Theory of Communication)》中提出的概念。他借用热力学中热熵的概念(热熵是表示分子状态混乱程度的物理量),解决了对信息的量化度量问题,也常用来对不确定性进行度量。
信息量与信息熵
信息量在数学上表示为 I ( X ) = − l o g P ( X ) I(X) = -logP(X) I(X)=−logP(X)。
信息熵则被定义为对平均不确定性的度量。一个离散随机变量 X X X的信息熵 H ( X ) H(X) H(X)定义为:
H ( X ) = ∑ X P ( X ) l o g 1 P ( X ) = − ∑ X P ( X ) l o g P ( X ) H(X) = \sum_{X}P(X)log\frac{1}{P(X)}= -\sum_{X}P(X)logP(X) H(X)=∑XP(X)logP(X)1=−∑XP(X)logP(X)
其中、约定 0 l o g ( 1 / 0 ) = 0 0log(1 / 0) = 0 0log(1/0)=0,对数若以2为底,则熵的单位是比特;若以 e e e为底,则其单位是奈特。若无特殊说明,则均采用比特为单位。
1、信息熵的本质是信息量的期望。
2、信息熵是对随机变量不确定性的度量。随机变量 X X X的熵越大,说明它的不确定性也越大。若随机变量退化为定值,则熵为0。
3、平均分布是“最不确定”的分布。
下面举两个例子来说明这一点。
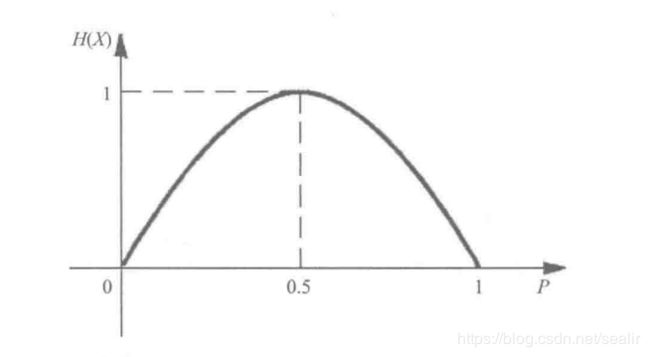
例1、考虑一个取值为0或1的随机变量 X X X,满足(0, 1)分布,记 p = P ( x = 1 ) p = P(x=1) p=P(x=1)。根据熵的定义,有:
H ( X ) = − p l o g ( p ) − ( 1 − p ) l o g ( 1 − p ) H(X) = -plog(p) - (1-p)log(1-p) H(X)=−plog(p)−(1−p)log(1−p)
如图,当 p = 0 p=0 p=0或 p = 1 p=1 p=1时,我们肯定地知道 X X X的取值,不确定性最小, H ( X ) = 0 H(X) = 0 H(X)=0。当 p = 0.5 p=0.5 p=0.5时,对 X X X的取值的不确定性达到最大,此时 H ( X ) = 1 H(X) = 1 H(X)=1。该例子验证了上面熵的性质。
例2、记 X X X、 Y Y Y和 Z Z Z分别为掷硬币、掷骰子,以及从54张扑克牌中随意抽取一张的结果。显然 X X X的不确定性最小, Y Y Y的不确定性居中,而 Z Z Z的不确定性最大。与之相应,这3个随机变量的熵之间也恰恰存在这样的关系,即 H ( X ) < H ( Y ) < H ( Z ) H(X) < H(Y) < H(Z) H(X)<H(Y)<H(Z)。
H ( X ) = ∑ 1 2 1 2 l o g ( 2 ) = l o g 2 H(X) = \sum_{1}^{2} \frac{1}{2} log(2) = log2 H(X)=∑1221log(2)=log2
H ( Y ) = ∑ 1 6 1 6 l o g ( 6 ) = l o g 6 H(Y) = \sum_{1}^{6} \frac{1}{6} log(6) = log6 H(Y)=∑1661log(6)=log6
H ( Z ) = ∑ 1 54 1 54 l o g ( 54 ) = l o g 54 H(Z) = \sum_{1}^{54} \frac{1}{54} log(54) = log54 H(Z)=∑154541log(54)=log54
用 ∣ X ∣ |X| ∣X∣来记作 X X X变量的取值个数,又称为变量的势。
熵的基本性质如下:
1、 H ( X ) > = 0 H(X) >= 0 H(X)>=0
2、 H ( X ) < = l o g ∣ X ∣ H(X) <= log|X| H(X)<=log∣X∣,等号成立的条件,当且仅当 X X X的所有取值 x x x有 P ( X = x ) = 1 ∣ X ∣ P(X=x) = \frac{1}{|X|} P(X=x)=∣X∣1。
互信息、联合熵、条件熵
1、互信息
如图,通过该图理解互信息比较容易。一般而言,信道中总是存在着噪声和干扰,信源发出消息 x x x,通过信道后信宿只可能收到由于干扰作用引起的某种变形 y y y。信宿收到 y y y后推测信源发出 x x x的概率,这一过程可由后验概率 p ( x ∣ y ) p(x|y) p(x∣y)来描述。相应的,信源发出 x x x的概率 p ( x ) p(x) p(x)称为先验概率。定义 x x x的后验概率与先验概率比值的对数为 y y y对 x x x的互信息量(简称互信息)。其公式如下:
互信息定义: I ( y , x ) = I ( y ) − I ( y ∣ x ) = l o g P ( y ∣ x ) P ( y ) I(y, x) = I(y) - I(y|x) = log \frac{P(y|x)}{P(y)} I(y,x)=I(y)−I(y∣x)=logP(y)P(y∣x)
互信息的性质如下:
1、互信息可以理解为,收信者收到信息 X X X后,对信源 Y Y Y的不确定性的消除。
2、互信息 = I I I(先验事件) - I I I(后验事件) = l o g 后 验 概 率 先 验 概 率 log\frac {后验概率}{先验概率} log先验概率后验概率。
3、互信息是对称的。
平均互信息: I ( X ; Y ) = ∑ X , Y P ( X , Y ) l o g P ( X , Y ) P ( X ) P ( Y ) I(X;Y) = \sum_{X,Y} \ P(X,Y)log\frac{P(X,Y)}{P(X)P(Y)} I(X;Y)=∑X,Y P(X,Y)logP(X)P(Y)P(X,Y)
平均互信息又称为信息增益。
2、联合熵
联合熵是借助联合分率分布对熵的自然推广,两个离散随机变量 X X X和 Y Y Y的联合熵定义为:
H ( X , Y ) = ∑ X , Y P ( X , Y ) l o g 1 P ( X , Y ) = − ∑ X Y P ( X , Y ) l o g ( X , Y ) H(X,Y) = \sum_{X,Y} \ P(X,Y)log \frac{1}{P(X,Y)} = -\sum_{XY} \ P(X,Y)log(X,Y) H(X,Y)=∑X,Y P(X,Y)logP(X,Y)1=−∑XY P(X,Y)log(X,Y)
3、条件熵
条件熵是利用概率分布对熵的一个延伸。随机变量 X X X的熵是用它的概率分布 P ( X ) P(X) P(X)来定义的。如果知道另一个随机变量 Y Y Y的取值为 y y y,那么 X X X的后验分布即为 P ( X ∣ Y = y ) P(X|Y=y) P(X∣Y=y)。利用条件分布可以定义给定 Y = y Y=y Y=y时 X X X的条件熵为:
H ( X ∣ Y = y ) = − ∑ X P ( X ∣ Y = y ) l o g P ( X ∣ Y = y ) H(X|Y=y) = -\sum_X P(X|Y=y)logP(X|Y=y) H(X∣Y=y)=−∑XP(X∣Y=y)logP(X∣Y=y)
熵 H ( X ) H(X) H(X)变量的是随机变量 X X X的不确定性,条件熵 H ( X ∣ Y = y ) H(X|Y=y) H(X∣Y=y)变量的则是已知 Y = y Y=y Y=y后, X X X的不确定性。
熵的链式规则:
H ( X , Y ) = H ( X ) + H ( Y ∣ X ) = H ( Y ) + H ( X ∣ Y ) H(X,Y) = H(X) + H(Y|X) = H(Y) + H(X|Y) H(X,Y)=H(X)+H(Y∣X)=H(Y)+H(X∣Y)
I ( X ; Y ) + H ( X , Y ) = H ( X ) + H ( Y ) I(X;Y) + H(X,Y) = H(X) + H(Y) I(X;Y)+H(X,Y)=H(X)+H(Y)
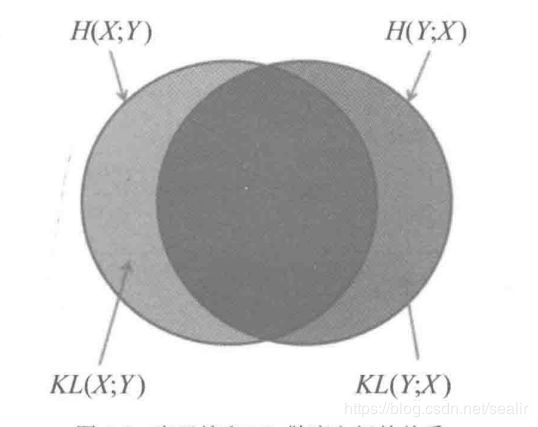
如图所示为联合熵、条件熵和互信息之间的关系:

边缘独立定理:从信息论角度为“边缘独立”这一概念提供了一个直观解释,即两个随机变量相互独立当且仅当它们之间的互信息为0。
接下来考虑3个变量 X X X、 Y Y Y和 Z Z Z之间的条件独立关系。条件熵 H ( X ∣ Z ) H(X|Z) H(X∣Z)是给定 Z Z Z时 X X X剩余的不确定性,如果进一步再给定 Y Y Y,则 X X X剩余的不确定性变为 H ( X ∣ Z , Y ) H(X|Z,Y) H(X∣Z,Y)。因此,这两者之差即是给定 Z Z Z时观测 Y Y Y的取值会带来的关于 X X X的信息量,即:
I ( X ; Y ∣ Z ) = H ( X ∣ Z ) − H ( X ∣ Z , Y ) I(X;Y|Z) = H(X|Z) - H(X|Z,Y) I(X;Y∣Z)=H(X∣Z)−H(X∣Z,Y)
称为给定 Z Z Z时 Y Y Y关于 X X X的信息,容易证明 I ( X ; Y ∣ Z ) = I ( Y ; X ∣ Z ) I(X;Y|Z) = I(Y;X|Z) I(X;Y∣Z)=I(Y;X∣Z)。于是, I ( X ; Y ∣ Z ) I(X;Y|Z) I(X;Y∣Z)也称为给定 Z Z Z时 X X X和 Y Y Y之间的条件互信息。
定理:对任意3个离散随机变量 X X X、 Y Y Y和 Z Z Z,有:
1、 I ( X , Y ∣ Z ) > = 0 I(X,Y|Z) >= 0 I(X,Y∣Z)>=0
2、 H ( X ∣ Y , Z ) < = H ( X ∣ Z ) H(X|Y,Z) <= H(X|Z) H(X∣Y,Z)<=H(X∣Z)
上述定理的意义在于,它从信息论的角度为随机变量之间的“条件独立”这一概念提供了一个直观解释,即给定 Z Z Z,两个随机变量 X X X和 Y Y Y相互条件独立,当且仅当它们的条件互信息为零,或者说, Y Y Y关于 X X X的信息已全部包含在 Z Z Z中,从而观测到 Z Z Z后,再对 Y Y Y进行的观测不会带来关于 X X X的更多信息。另外,如果 X X X和 Y Y Y在给定 Z Z Z时相互不独立,则 H ( X ∣ Z , Y ) = H ( X ∣ Z ) H(X|Z,Y) = H(X|Z) H(X∣Z,Y)=H(X∣Z),即在已知 Z Z Z的基础上对 Y Y Y的进一步观测将会带来关于 X X X的新信息,从而降低 X X X的不确定性。
交叉熵和KL散度
1、交叉熵
H ( P ; Q ) = − ∑ P p ( Z ) l o g P q ( Z ) H(P;Q) = -\sum P_p(Z)logP_q(Z) H(P;Q)=−∑Pp(Z)logPq(Z)
1、交叉熵常用来衡量两个概率分布的差异性。
2、在Logistic中的交叉熵为其代价函数。
2、相对熵与变量独立
相对熵定义:对定义随机变量 X X X的状态空间 Ω x \Omega_x Ωx上的两个概率分布 P ( X ) P(X) P(X)和 Q ( X ) Q(X) Q(X),可以用相对熵来度量它们之间的差异,即有:
K L ( P , Q ) = ∑ X P ( X ) l o g P ( X ) Q ( X ) KL(P,Q) = \sum_X P(X)log \frac{P(X)}{Q(X)} KL(P,Q)=∑XP(X)logQ(X)P(X)
其中,约定 0 l o g 0 q = 0 0log\frac{0}{q} = 0 0logq0=0; p l o g p 0 = ∞ plog\frac{p}{0} = \infty plog0p=∞, ∀ p > 0 \forall p > 0 ∀p>0。 K L ( P , Q ) KL(P,Q) KL(P,Q)又称为 P ( X ) P(X) P(X)和 Q ( X ) Q(X) Q(X)之间的 K L KL KL散度。但严格来讲它不是一个真正意义上的距离,因为 K L ( P , Q ) ≠ K L ( Q , P ) KL(P,Q) \neq KL(Q,P) KL(P,Q)̸=KL(Q,P)。
定理:设 P ( X ) P(X) P(X)和 Q ( X ) Q(X) Q(X)为定义在某个变量 X X X的状态空间 Ω x \Omega_x Ωx上的两个概率分布,则有:
K L ( P , Q ) > = 0 KL(P,Q) >= 0 KL(P,Q)>=0
其中,当且仅当 P P P和 Q Q Q相同,即 P ( X = x ) = Q ( X = x ) P(X=x) = Q(X=x) P(X=x)=Q(X=x), ∀ x ε Ω x \forall x \ \varepsilon \ \Omega_x ∀x ε Ωx时等号成立。
推论,对于满足 ∑ f ( X ) > 0 \sum f(X) > 0 ∑f(X)>0的非负函数 f ( X ) f(X) f(X),定义概率分布 P ∗ ( X ) P^*(X) P∗(X)为:
P ∗ ( X ) = f ( X ) ∑ X f ( X ) P^*(X) = \frac {f(X)} {\sum_X \ f(X)} P∗(X)=∑X f(X)f(X)
那么,对于任意其他的概率分布 P ( X ) P(X) P(X),则有:
∑ X f ( X ) l o g P ∗ ( X ) ⩾ ∑ X f ( X ) l o g P ( X ) \sum_X f(X)logP^*(X) \geqslant \sum_X f(X)logP(X) ∑Xf(X)logP∗(X)⩾∑Xf(X)logP(X)
其中,当且仅当 P ∗ P^* P∗与 P P P相同时等号成立。
定理:互信息与变量独立之间的两个关系,首先有如下定理,对任意两个离散随机变量 X X X和 Y Y Y有:
1、 I ( X , Y ) ⩾ 0 I(X,Y) \geqslant 0 I(X,Y)⩾0
2、 H ( X ∣ Y ) ≤ H ( X ) H(X|Y) \leq H(X) H(X∣Y)≤H(X)
上述两式当且仅当 X X X与 Y Y Y相互独立时等号成立。
本文摘自《NLP汉语自然语言处理原理与实践》