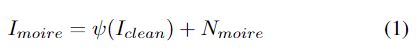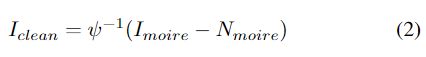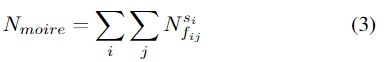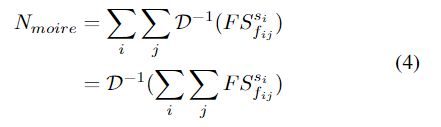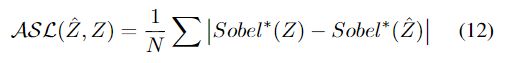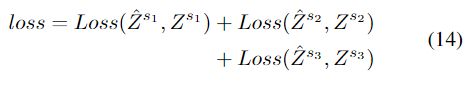CVPR2020 | 对数字屏幕拍照时的摩尔纹怎么去除?
点击上方“AI算法修炼营”,选择“星标”公众号
精选作品,第一时间送达
本文收录于CVPR2020,是华为诺亚方舟研究院的成果,主要解决的是,去除对数字屏幕拍照产生摩尔纹,有一定的应用价值。
论文地址:https://arxiv.org/pdf/2004.00406.pdf
代码地址(Tensorflow+Keras实现):https://github.com/zhenngbolun/Learnbale_Bandpass_Filter
Image demoireing是涉及纹理和颜色恢复的多方面图像恢复任务。在本文中,提出了一种新颖的多尺度bandpass 卷积神经网络(MBCNN)来解决这个问题。作为端到端解决方案,MBCNN分别解决了两个子问题。对于纹理恢复子问题,提出了一个可学习的带通滤波器(LBF),以了解去除摩尔纹之前的频率。对于颜色恢复子问题,提出了两步色调映射策略,该策略首先应用全局色调映射来校正全局色彩shift,然后对每个像素执行颜色的局部微调。通过消融研究,我们证明了MBCNN不同组件的有效性。在两个公共数据集上的实验结果表明,本文的方法大大优于最新方法(在PSNR方面超过2dB)。
简介
数字屏幕在现代日常生活中无处不在:我们在家里有电视屏幕,在办公室有笔记本电脑/台式机屏幕,在公共场所有大尺寸LED屏幕。拍摄这些屏幕的图片以快速保存信息已成为一种惯例。然而,在对这些屏幕拍照的时候通常会出现波纹图像,从而降低了照片的图像质量。当两个重复的图案相互干扰时,出现摩尔纹图案。在拍摄屏幕图片的情况下,相机滤色镜阵列(CFA)会干扰屏幕的亚像素布局。
与去噪、去马赛克、颜色恒定、锐化等其他图像修复问题不同,人们对图像去伪存真(demireing)的关注较少,它是指从被摩尔纹污染的图像中恢复基本的干净图像。这个问题在很大程度上仍然是一个未解决的问题,由于摩尔纹图案在频率、形状、颜色等方面的巨大变化。
最近的很多工作试图通过多尺度设计来消除不同频段的摩尔纹。DMCNN 提出使用具有多分辨率分支的多尺度CNN处理摩尔纹图案,并对不同尺度的输出求和以获得最终输出。MDDM 通过引入基于动态特征编码器的自适应实例规范化改进了DMCNN。DCNN提出了一种从粗到细的结构来去除两尺度的摩尔条纹。对粗尺度结果进行上采样,并将其与细尺度输入连接起来,以进行进一步的残差学习。MopNet 使用多尺度特征聚合子模块来处理复杂频率,并使用另外两个子模块来处理边沿和预定义的波纹类型。本文的模型还采用了针对三个不同比例的分支的多比例设计。在不同尺度之间,本文的模型采用渐进式上采样策略以平滑地提高分辨率。
本文的方法:Multiscale bandpass CNN
数码相机捕获的含摩尔纹的图像可以建模为:
其中ψ-1是ψ的反函数,在图像处理领域被称为色调映射函数。以此模型建模,图像去摩尔纹任务可以分为两步,即摩尔条纹去除和色调映射。
1、Multiscale bandpass CNN
为了对遥感图像中的物体分割前景进行显式建模,本文提出了一种前景感知关系网络(FarSeg),如图2所示。FarSeg由特征金字塔网络(FPN)、前景场景(F-S)关系模块、轻量级解码器和前景感知(F-A)优化组成。FPN负责多尺度对象分割。在F-S关系模块中,首先将误报问题表述为前景中缺乏区分性信息的问题,然后介绍潜在场景语义和F-S关系以改善对前景特征的区分。轻量级解码器仅设计用于恢复语义特征的空间分辨率。为了使网络在训练过程中集中在前景上,提出了F-A优化来减轻前景背景不平衡的问题。
1.1、 Multi-Branch Encoder
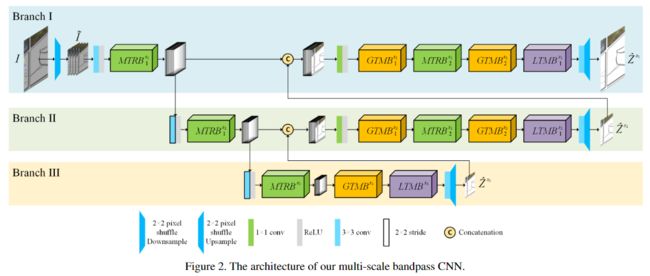
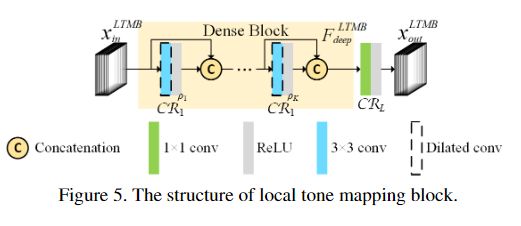
整体的模型在三个scales上工作,并具有三种不同类型的blocks,分别是波纹纹理去除块(MTRB),全局色调映射块(GTMB)和局部色调映射块(LTMB)。
首先将具有h×w×c形状的输入图像I可逆地向下采样为四个h/2×w/2×4c形状的子图像。下面的网络由三个分支组成,每个分支用于恢复特定比例的波纹图像,同时每个分支顺序地执行摩尔纹去除和色调映射,最终输出放大后的图像,并将其融合到更小比例的分支中。在分支I和II中,将当前分支的特征和较粗的缩放分支的输出特征融合后,将其他GTMB和MTRB堆叠在一起,以消除缩放比例引起的纹理和颜色错误。
def MBCNN(nFilters, multi=True):
conv_func = conv_relu
def pre_block(x, d_list, enbale = True):
t = x
for i in range(len(d_list)):
_t = conv_func(t, nFilters, 3, dilation_rate=d_list[i])
t = layers.Concatenate(axis=-1)([_t,t])
t = conv(t, 64, 3)
t = adaptive_implicit_trans()(t)
t = conv(t,nFilters*2,1)
t = ScaleLayer(s=0.1)(t)
if not enbale:
t = layers.Lambda(lambda x: x*0)(t)
t = layers.Add()([x,t])
return t
def pos_block(x, d_list):
t = x
for i in range(len(d_list)):
_t = conv_func(t, nFilters, 3, dilation_rate=d_list[i])
t = layers.Concatenate(axis=-1)([_t,t])
t = conv_func(t, nFilters*2, 1)
return t
def global_block(x):
t = layers.ZeroPadding2D(padding=(1,1))(x)
t = conv_func(t, nFilters*4, 3, strides=(2,2))
t = layers.GlobalAveragePooling2D()(t)
t = layers.Dense(nFilters*16,activation='relu')(t)
t = layers.Dense(nFilters*8, activation='relu')(t)
t = layers.Dense(nFilters*4)(t)
_t = conv_func(x, nFilters*4, 1)
_t = layers.Multiply()([_t,t])
_t = conv_func(_t, nFilters*2, 1)
return _t
output_list = []
d_list_a = (1,2,3,2,1)
d_list_b = (1,2,3,2,1)
d_list_c = (1,2,2,2,1)
x = layers.Input(shape=(None, None, 3)) #16m*16m
_x = Space2Depth(scale=2)(x)
t1 = conv_func(_x,nFilters*2,3, padding='same') #8m*8m
t1 = pre_block(t1, d_list_a, True)
t2 = layers.ZeroPadding2D(padding=(1,1))(t1)
t2 = conv_func(t2,nFilters*2,3, padding='valid',strides=(2,2)) #4m*4m
t2 = pre_block(t2, d_list_b,True)
t3 = layers.ZeroPadding2D(padding=(1,1))(t2)
t3 = conv_func(t3,nFilters*2,3, padding='valid',strides=(2,2)) #2m*2m
t3 = pre_block(t3,d_list_c, True)
t3 = global_block(t3)
t3 = pos_block(t3, d_list_c)
t3_out = conv(t3, 12, 3)
t3_out = Depth2Space(scale=2)(t3_out) #4m*4m
output_list.append(t3_out)
_t2 = layers.Concatenate()([t3_out,t2])
_t2 = conv_func(_t2, nFilters*2, 1)
_t2 = global_block(_t2)
_t2 = pre_block(_t2, d_list_b,True)
_t2 = global_block(_t2)
_t2 = pos_block(_t2, d_list_b)
t2_out = conv(_t2, 12, 3)
t2_out = Depth2Space(scale=2)(t2_out) #8m*8m
output_list.append(t2_out)
_t1 = layers.Concatenate()([t1, t2_out])
_t1 = conv_func(_t1, nFilters*2, 1)
_t1 = global_block(_t1)
_t1 = pre_block(_t1, d_list_a, True)
_t1 = global_block(_t1)
_t1 = pos_block(_t1, d_list_a)
_t1 = conv(_t1,12,3)
y = Depth2Space(scale=2)(_t1) #16m*16m
output_list.append(y)
if multi != True:
return models.Model(x,y)
else:
return models.Model(x,output_list)
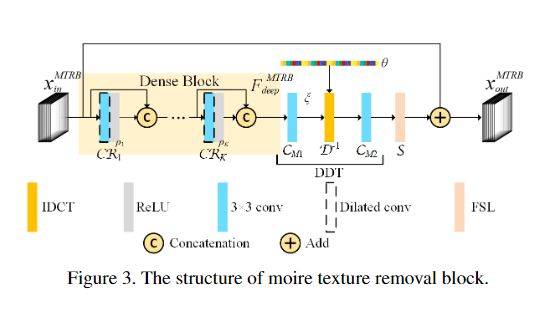
1.2、Moire texture removal
摩尔纹可以表示为:
按照这种公式,我们可以先估计不同尺度和频率的波纹纹理的分量,然后基于所有估计的分量重建波纹纹理。Block-DCT是处理频率相关问题的有效方法。
其中D表示Block-DCT函数。
Learnable Bandpass Filter
受隐式DCT的启发,可以用深度CNN直接估计 implicit frequency spectrum(IFS) 。由于变换都是线性的,因此可以用一个简单的卷积层来建模。由于Moire纹理的频谱总是有规律的,我们可以使用带通滤波器来放大某些频率,减弱其他频率。然而,在建模之前我们很难得到频谱,因为在不同的尺度上,会有几个频率,而且它们也会相互影响。为了解决这个问题,提出了一种可学习的带通滤波器(LBF)来学习摩尔纹图像的先验。LBF为每一个频率引入了一个可学习的权重。
class adaptive_implicit_trans(layers.Layer):
def __init__(self, **kwargs):
super(adaptive_implicit_trans, self).__init__(**kwargs)
def build(self, input_shape):
conv_shape = (1,1,64,64)
self.it_weights = self.add_weight(
shape = (1,1,64,1),
initializer = initializers.get('ones'),
constraint = constraints.NonNeg(),
name = 'ait_conv')
kernel = np.zeros(conv_shape)
r1 = sqrt(1.0/8)
r2 = sqrt(2.0/8)
for i in range(8):
_u = 2*i+1
for j in range(8):
_v = 2*j+1
index = i*8+j
for u in range(8):
for v in range(8):
index2 = u*8+v
t = cos(_u*u*pi/16)*cos(_v*v*pi/16)
t = t*r1 if u==0 else t*r2
t = t*r1 if v==0 else t*r2
kernel[0,0,index2,index] = t
self.kernel = k.variable(value = kernel, dtype = 'float32')
def call(self, inputs):
#it_weights = k.softmax(self.it_weights)
#self.kernel = self.kernel*it_weights
self.kernel = self.kernel*self.it_weights
y = k.conv2d(inputs,
self.kernel,
padding = 'same',
data_format='channels_last')
return y
def compute_output_shape(self, input_shape):
return input_shape
1.3 Tone mapping 色调映射
RGB颜色空间是一个非常大的空间,包含256的3次方种颜色,因此很难进行逐点色调映射。观察到摩尔纹图像和干净图像之间存在颜色偏移,本文提出了一种两步色调映射策略,其中包含两种类型的色调映射块:全局色调映射块(GTMB)和局部色调映射块(LTMB)。
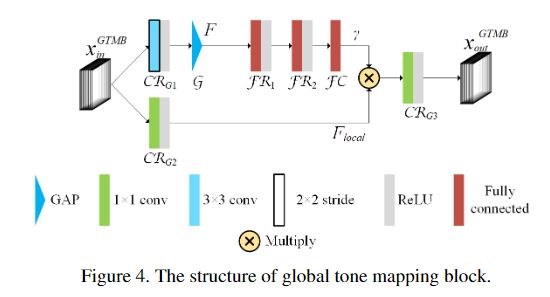
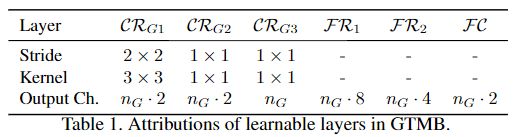
全局色调映射块Global tone mapping block
注意力机制已经被证明在许多任务中是有效的,并且已经提出了几种通道注意模块。GTMB可以看作是一个通道注意模块。然而,GTMB与现有的通道注意模块在几个方面有所不同。 首先,现有的通道注意力块总是由一个Sigmoid单元激活,而GTMB中的γ没有这样的约束。其次,通道注意力是直接应用在现有通道注意力块的输入上,而GTMB中的γ是应用在局部特征Flocal上。最后,现有的通道注意力模块的目的是进行自适应的channel-wise特征重新校准;GTMB的目标是进行全局的颜色偏移,避免不规则和不均匀的局部颜色伪影。
局部色调映射块Local tone mapping block
2、 损失函数
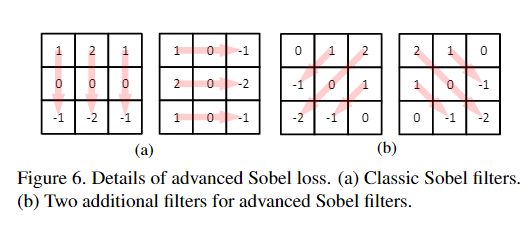
在本文中,将L1损失用作基本损失函数,因为已经证明 L1损失比L2损失对图像恢复任务更有效。但是,L1损失本身是不够的,因为它是无法提供结构信息的逐点损失,而摩尔纹是 structural artifact。本文提出了Advanced Sobel Loss(ASL)来解决此问题。
与经典Sobel Loss相比,ASL提供了两个额外的45°方向Loss,它们可以提供更丰富的结构信息。
总的损失函数为:
实验与结果
数据集: LCDMoire(Aim 2019 challenge on image demoreing: datasetand study. InICCVW, 2019)、TIP2018( Moire photorestoration using multiresolution convolutional neural net-works.)
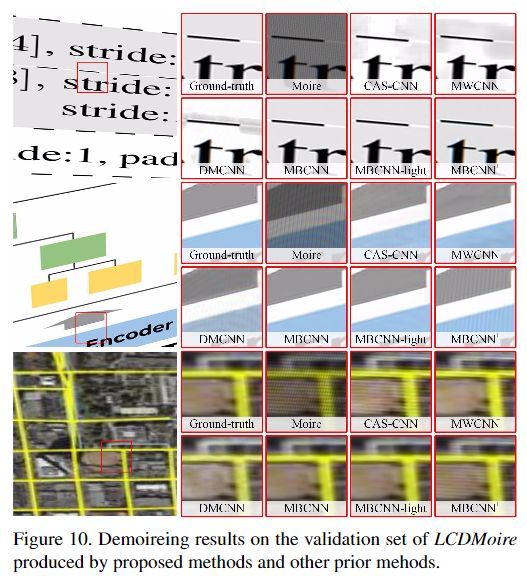
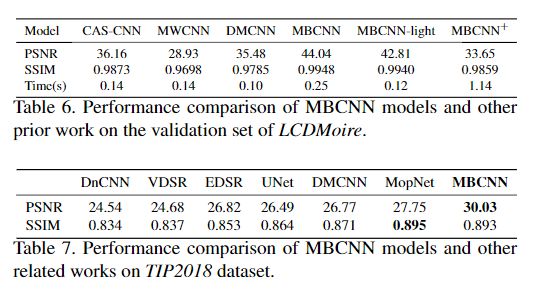
实验结果
更多细节可参考论文原文。
![]()
![]()
![]()