Leetcode 22: 括号生成

题目

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例：

输入：n = 3
输出：[
       "((()))",
       "(()())",
       "(())()",
       "()(())",
       "()()()"
     ]

分析

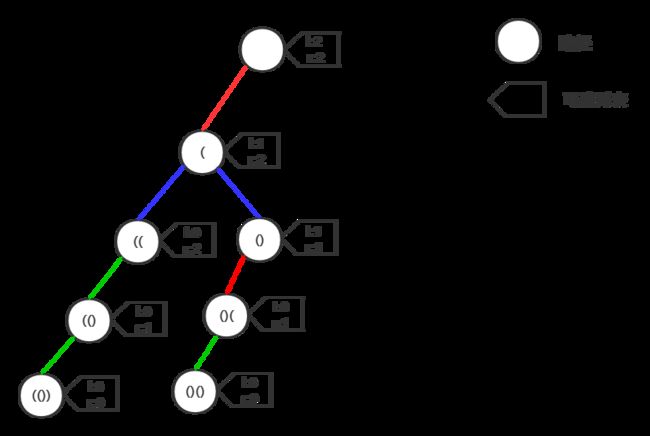
该题目也是利用回溯法的经典题目，与电话号码的字母组合十分类似，重要的是画出深度优先搜索树，并找到路径和可选列表。

用 left， right 表示可选列表，sb 记录当前的路径。

如果 left == 0 && right == 0 说明到达了叶子结点，保存答案，return。

如果 left == right && left > 0, 是图中红线情况，只能添加一个左括号。

如果 left < right && left > 0, 是图中的蓝线情况，可以添加一个左括号，也可以添加一个右括号。

如果 left == 0 && right > 0, 是图中绿线情况，只能添加一个右括号。

left = 0		left > 0
right = 0	right > 0	right = left	right > left
return	添加 )	添加 (	添加 ( 、 ）

代码

class Solution {
    public List generateParenthesis(int n) {
        List res = new ArrayList<>();
        if (n == 0) return res;
        permute(res, new StringBuilder(), n, n);
        return res;
    }
    // left 记录当前可用左括号的数目，right 记录当前可用右括号的数目
    private void permute(List res, StringBuilder sb, int left, int right) { 
        if (left == 0 && right == 0) {
            res.add(sb.toString());
            return;
        }
        if (left == right) {
            doLeft(res, sb, left, right);
        } else if (left < right && left > 0) {
            doLeft(res, sb, left, right);
            doRight(res, sb, left, right);
        } else { // left == 0;
            doRight(res, sb, left, right);
        }
    }
    private void doLeft(List res, StringBuilder sb, int left, int right) {
        sb.append('(');
        permute(res, sb, left - 1, right);
        sb.deleteCharAt(sb.length() - 1);
    }
    private void doRight(List res, StringBuilder sb, int left, int right) {
        sb.append(')');
        permute(res, sb, left, right - 1);
        sb.deleteCharAt(sb.length() - 1);
    }
}

left = 0		left > 0
right = 0	right > 0(left)	right = left	right > left
return	添加 )	添加 (	添加 ( 、 ）

由上面的表格，可以发现，left 只要大于 0，就可以添加左括号；只要 right > left， 就可以添加右括号。

所以将代码可以简化成：

class Solution {
    public List generateParenthesis(int n) {
        List res = new ArrayList<>();
        if (n == 0) return res;
        permute(res, new StringBuilder(), n, n);
        return res;
    }
    // left 记录当前可用左括号的数目，right 记录当前可用右括号的数目
    private void permute(List res, StringBuilder sb, int left, int right) { 
        if (left == 0 && right == 0) {
            res.add(sb.toString());
            return;
        }
        if (left > 0) {
            sb.append('(');
            permute(res, sb, left - 1, right);
            sb.deleteCharAt(sb.length() - 1);
        }
        if (left < right) {
            sb.append(')');
            permute(res, sb, left, right - 1);
            sb.deleteCharAt(sb.length() - 1);
        }
    }
}

更多关于回溯法的内容见刷题模板。