erl_tree-avl Trees平衡二叉查找树
(AVL—— 发明者为Adel’son-Vel’skii 和 Landis)
前面章分析过gb_tree 的插入不是立即平衡的,在查找效率上最坏情况有可能出现O(n), 如何解决这样的问题呢,关键是在减少树的深度,正是基于这个想法,平衡二叉树出现了。
平衡二叉查找树,又称 AVL树。 它除了具备二叉查找树的基本特征之外,还具有一个非常重要的特点:它 的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值(平衡因子 ) 不超过1。 也就是说AVL树每个节点的平衡因子只可能是-1、0和1(左子树高度减去右子树高度)。
那么如何是二叉查找树在添加数据的同时保持平衡呢?基本思想就是:当在二叉排序树中插入一个节点时,首先检查是否因插入而破坏了平衡,若 破坏,则找出其中的最小不平衡二叉树,在保持二叉排序树特性的情况下,调整最小不平衡子树中节点之间的关系,以达 到新的平衡。所谓最小不平衡子树 指离插入节点最近且以平衡因子的绝对值大于1的节点作为根的子树。
avl tree 查找,循环那些操作和gb_trees 基本是一样的就是在插入删除上的平衡的区别。
下面主要分析avl_tree 的旋转平衡:
1、RR型:平衡二叉树某一节点的右孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向左旋转一次即可,如图所示,原A右孩子B变为父结点,A变为其左孩子,而原B的左子树Blh将变为A的右子树。

2、LL型:平衡二叉树某一节点的左孩子的左子树上插入一个新的节点,使得该节点不再平衡。这时只需要把树向右旋转一次即可,如图所示,原A的左孩子B变为父结点,A变为其右孩子,而原B的右子树变为A的左子树,注意旋转之后Brh是A的左子树(图上忘在A于Brh之间标实线)

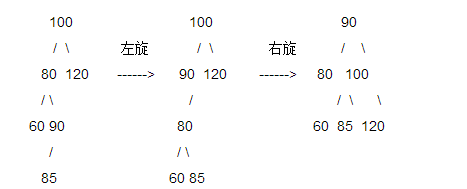
3、LR型: 平衡二叉树某一节点的左孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时需要旋转两次,仅一次的旋转是不能够使二叉树再次平衡。如图所示,在B节点按照RR型向左旋转一次之后,二叉树在A节点仍然不能保持平衡,这时还需要再向右旋转一次。
4、RL型: 平衡二叉树某一节点的右孩子的左子树上插入一个新的节点,使得该节点不再平衡。同样,这时需要旋转两次,旋转方向刚好同LR型相反。

性能分析:avl_tree 不会出现O(n)情况,查找复杂度为O(logN),但是由于高度的平衡,插入和删除的代价加大,所以该类型适合在多查找,少变动的场景。
实现代码:
%%=========avl Trees==============
%% avl_trees={Size,Tree}
%% Tree= {Key, Value, Smaller, Bigger} |nil
%% Smaller=Tree
%% Bigger= Tree
%% avl tree 和通用二叉查找树 的区别在与插入 删除保持
%% 左右子树的深度只差绝对值不超过1
avl_tree_init()->
gb_trees:empty().
%%计算深度差,平衡整棵树
avl_tree_insert(Key, Val, {S, T}) when is_integer(S) ->
S1 = S+1,
{S1, avl_insert_2(Key, Val, T,[])}.
%%PassNodeTrack :[{Tree,dir}]
%% SLL={5,{100,1,{85,2,{60,3,nil,nil},{90,5,nil,nil}},{120,6,nil,nil}}}.
%%tree:avl_tree_insert(80,4,S).
%% SRR={5,{80,1,{60,2,nil,nil},{90,3,{85,4,nil,nil},{120,5,nil,nil}}}}.
%% tree:avl_tree_insert(100,6,SRR).
%% SLR={5,{100,1,{80,2,{60,3,nil,nil},{90,4,nil,nil}},{120,6,nil,nil}}}.
%% tree:avl_tree_insert(85,5,SLR).
%%SRL={5,{80,1,{60,2,nil,nil},{100,3,{85,4,nil,nil},{120,6,nil,nil}}}}.
%% tree:avl_tree_insert(90,6,SRL).
avl_insert_2(Key, Value, {Key1, V, Smaller, Bigger},PassNodeTrack) when Key < Key1 ->
avl_insert_2(Key, Value, Smaller,[{{Key1, V, nil, Bigger},0}|PassNodeTrack]);
avl_insert_2(Key, Value, {Key1, V, Smaller, Bigger},PassNodeTrack) when Key > Key1 ->
avl_insert_2(Key, Value, Bigger,[{{Key1, V, Smaller, nil},1}|PassNodeTrack]);
avl_insert_2(Key, Value, nil,PassNodeTrack) ->
NewPassNodeTrack = [{{Key, Value, nil, nil},2}|PassNodeTrack],
avl_insert_2_1(NewPassNodeTrack);
avl_insert_2(Key, _, _, _) ->
erlang:error({key_exists, Key}).
avl_insert_2_1(NewPassNodeTrack) when length(NewPassNodeTrack) < 4->
avl_insert_2_2(NewPassNodeTrack);%%向上重构树
avl_insert_2_1(NewPassNodeTrack)->
{HNodeTrack,TNodeTrack} = lists:split(4,NewPassNodeTrack),
NTree = avl_insert_2_2(HNodeTrack),
NTree1 = avl_insert_2_2_turn(NTree,HNodeTrack),
avl_insert_2_2([{NTree1,2}|TNodeTrack]).
%%判断树的旋转
avl_insert_2_2_turn({K,V,ST,BT} = Tree,HNodeTrack)->
case abs(get_depth1(ST,0)-get_depth1(BT,0)) > 1 of %%判断是否不平衡了
false->
{K,V,ST,BT};
_->
DirList = [Dir||{_,Dir}<-HNodeTrack],
avl_insert_2_2_turn1(Tree,DirList)
end.
%%旋转方式
%%RR 左旋
avl_insert_2_2_turn1(Tree,[_,_,1,1])->
avl_tree_balance_left_turn(Tree);
%%LL 右旋
avl_insert_2_2_turn1(Tree, [_,_,0,0]) ->
avl_tree_balance_right_turn(Tree);
%%LR型 左旋 --> 右旋
avl_insert_2_2_turn1(Tree, [_,_,1,0]) ->
avl_tree_balance_lr_turn(Tree);
%% RL型 右旋 --> 左旋
avl_insert_2_2_turn1(Tree, [_,_,0,1]) ->
avl_tree_balance_rl_turn(Tree).
%%向上重构树
avl_insert_2_2(HNodeTrack)->
avl_insert_2_2_1(HNodeTrack,nil).
avl_insert_2_2_1([],NewTree)->
NewTree;
avl_insert_2_2_1([{{K,V,ST,BT},2}|TL], nil) ->
avl_insert_2_2_1(TL,{K,V,ST,BT});
avl_insert_2_2_1([{{K,V,_ST,BT},0}|TL], NewTree) ->
avl_insert_2_2_1(TL,{K,V,NewTree,BT});
avl_insert_2_2_1([{{K,V,ST,_BT},1}|TL], NewTree) ->
avl_insert_2_2_1(TL,{K,V,ST,NewTree}).
avl_insert_1(Key, Value, {Key1, V, Smaller, Bigger}) when Key < Key1 ->
{Key1, V, avl_insert_1(Key, Value, Smaller), Bigger};
avl_insert_1(Key, Value, {Key1, V, Smaller, Bigger}) when Key > Key1 ->
{Key1, V, Smaller, avl_insert_1(Key, Value, Bigger)};
avl_insert_1(Key, Value, nil) ->
{Key, Value, nil, nil};
avl_insert_1(Key, _, _) ->
erlang:error({key_exists, Key}).
avl_tree_lookup(Key, Tree)->
gb_trees:lookup(Key, Tree).
avl_tree_get(Key, Tree)->
gb_trees:get(Key, Tree).
%%其他语言结构的avl平衡是不用重构树的通过四种旋转实现:LL LR RR RL
avl_tree_balance(Tree1) ->
gb_trees:balance(Tree1).
%% RR 当树中节点X的右孩子的右孩子上插入新元素,且平衡因子从-1变成-2后,就需要绕节点X进行左旋转。
%% S={80,1,{60,2,nil,nil},{90,3,{85,4,nil,nil},{120,5,{100,6,nil,nil},nil}}}.
avl_tree_balance_left_turn({Key, V, ST, nil})->
{Key, V, ST, nil};
avl_tree_balance_left_turn({Key, V, ST, {Key1, V1, ST1, BT1}}) ->
{Key1, V1, {Key, V, ST,ST1}, BT1}.
%% LL 当树中节点X的左孩子的左孩子上插入新元素,且平衡因子从1变成2后,就需要绕节点X进行右旋转。
%% S1={100,1,{85,2,{60,3,nil,{80,4,nil,nil}},{90,5,nil,nil}},{120,6,nil,nil}}.
avl_tree_balance_right_turn({Key, V, nil, BT})->
{Key, V, nil, BT};
avl_tree_balance_right_turn({Key, V, {Key1, V1, ST1, BT1},BT }) ->
{Key1, V1, ST1,{Key, V, BT1,BT}}.
%% LR 平衡二叉树某一节点的左孩子的右子树上插入一个新的节点,使得该节点不再平衡。这时需要旋转两次,仅一次的
%% 旋转是不能够使二叉树再次平衡。如图所示,在B节点按照RR型向左旋转一次之后,二叉树在A节点仍然不能保持平衡,
%% 这时还需要再向右旋转一次。
%% S2={100,1,{80,2,{60,3,nil,nil},{90,4,{85,5,nil,nil},nil}},{120,6,nil,nil}}.
avl_tree_balance_lr_turn({Key, V, nil, BT})->
{Key, V, nil, BT};
avl_tree_balance_lr_turn({Key, V, ST, BT}) ->
NewLetf = avl_tree_balance_left_turn(ST),
avl_tree_balance_right_turn({Key, V, NewLetf, BT}).
%% RL 平平衡二叉树某一节点的右孩子的左子树上插入一个新的节点,使得该节点不再平衡。同样,这时需要旋转两次,旋转方向刚好同LR型相反。
%% S3={80,1,{60,2,nil,nil},{100,3,{85,4,nil,{90,6,nil,nil}},{120,6,nil,nil}}}.
avl_tree_balance_rl_turn({Key, V, ST, nil})->
{Key, V, ST, nil};
avl_tree_balance_rl_turn({Key, V, ST, BT}) ->
NewR = avl_tree_balance_right_turn(BT),
avl_tree_balance_left_turn({Key, V, ST, NewR}).
%% %%由于节点删除操作并不会增加树的高度,所以节点删除之后并没有进行再平衡.
avl_tree_delete(Key, Tree1)->
gb_trees:delete(Key, Tree1).
get_depth(Tree1)->
{_Size, {_K, _V, Smaller, Larger}}=Tree1,
{get_depth1(Smaller,0),get_depth1(Larger,0)}.
get_depth1(nil,C)->
C;
get_depth1({_, _, Smaller, Larger}, C) ->
Max = max(get_depth1(Smaller,0),get_depth1(Larger,0)),
C+Max+1.
%%=========avl Trees==============