《（数学篇）》 复数运算
【译文连载】《（数学篇）》——第六章
复数运算
虚数有一个直观化的解释：它把数字“旋转”，就像负数把数字做了“镜像”一样。这种深刻的见解使得我们理解复数的元算变得十分简单并且清晰，而且也可以很好的检查一下你是否学会了这种见解。以下是我们的作弊表：
这一章我们将逐一检验一遍我们的直观化的解释。
6.1 复变量
在常规代数中，我们经常说“x=3”，这样很好——有一个变量x，它的值是3.而在复数中，我们就会发现：有两个维度需要讨论。写下：
z=3+4i
我们就是在说有一个变量z，它有两部分：3（实数部分）与4i（虚数部分）。一个数有两部分看上去有些怪，但是我们已经用过这种表示方法了。我们经常会写：
y有一个整数部分（3）与一个分数部分（0.4或4/10）并不会影响我们理解它。Y是两部分的组合。复数也与之类似：在一个变量中它包含有实数部分与虚数部分（通常缩写为Re与Im）。
不幸的是，我们没有办法把它们“合起来”记作一个数（像3.4那样）。我有一个办法把用黑笔把虚数部分垂直的写在虚数上方，但是这种方法并不流行。所以我们还是继续使用“a+bi”的形式吧。
6.2 测量大小
因为复数有两个独立的数轴，我们发现它的大小可以使用勾股定理：
那么，复数3+4i的大小就是5。通常记作：|z|。
看起来很像是绝对值吧？其实从某种角度来看，它就是绝对值。|z|描述了复数距离零点的距离，就像是绝对值表示负数距离零点的距离一样。
6.3 复数的加法与减法
我们通常见到的加法可以被认为是“移动”一段数字而得到。复数的加法也可以这样类比，不过我们有两个维度（实数与虚数）可以移动。举个例子：
(3+4i)与(-1+i)相加就可以得到2+5i。
再一次的，这种可视化的解释帮助我们理解“独立的部分”是如何组合在一起的：实部与虚部各自处理再组合就可以了。
减法就是加法的逆——就是把它向相反的方向移动。减去(1+i)就是加上-1·(1+i)，或者是加上(-1-i)。
6.4 复数的乘法
这里数学就会变得很有趣。我们把两个复数（x，y）相乘得到z：
- 角度相加：角度（z）＝角度（x）+角度（y）
- 长度相乘：|z|=|x|+|y|
这就是说，z的角度是x的角度与y的角度的和，而长度就是它们的乘积。无论你相信与否，复数的这种性质帮了数学很大的忙！
长度相乘有它的意义——我们在一般的乘法中就是这么做的（3×4就是把3跟4的长度相乘）。角度的相加需要更详细的讨论，我们以后再谈（很好奇吗？看看正余弦函数是如何相加的，并把它们与(a+bi)·(c+di)比较一下）。
现在举另一个例子：我们把z＝3+4i乘以它自己。在做数学运算前，我们已经知道：
- 长度的结果会是25.因为z的长度为5，所以|z|·|z|＝25
- 角度的结果是大于90度。因为3+4i的角度大于45度（因为3+3i正好是45度），所以翻倍后比90度大。
接下来我们做数学运算：
(3+4i)·（3+4i）＝9+16i2 +24i＝-7+24i
现在来检查一下我们预测：
- 长度：
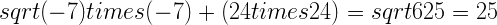跟我们的预测相符 - 角度：因为-7是负的而24i是个正的， 我们便知道我们要“向后并向上”，这就是说将跨过90度（“直直的”）。专业一点就是，我们计算arctan(24/-7)=106.2度（记住我们在第二象限）。这个也验证了我们的猜想。
漂亮。我们做数学运算时，还可以用我们关于旋转与大小的直观化认识来帮助我们检查结果。如果最后的结果小于90度（比如说，向前又向上），或者我们的长度不是25，我们便知道计算出了一些问题。
6.5 复数的除法
除法就是乘法的逆运算。就像减法是加法的逆运算一样。复数相除时（x/y），我们可以知道：
- 角度相减：角度（z）＝角度（x）－角度（y）
- 长度相除：|z|=|x|/|y|
看起来很不错。现在让我们做一做这个除法：
(3+4i)/(1+i)
呃，该从哪里开始呢？我们应该怎么做这个除法呢？通常的代数解法并不能帮不上什么忙，更不用说还有一个古怪的i（先生，先生，你知道1/i＝－i吗？两边同乘以i再看看一看啊。）幸好我们还有捷径可走。
6.6 引入复数的共轭
我们做复数除法的第一个目标就是把角度相减。我们怎么做呢？乘以与它相反的角度！这就会“加上”一个负的角度，等价于做了一次角度减法。
不再是z+bi，现在考虑以下z* ＝a-bi，叫作“复数共轭”。实部相等，但是虚部是一个“镜像”。复数共轭或者说“想象的一种反射”有着相同的长度，但是角度相反！
所以，乘以a-bi就是减去一个角度。很简洁。
复数共轭用星号（z* ）或者是横线表示(
)——数学家喜欢争论这些表示法的好坏。不管哪种表示方法，复数的共轭都是把它们的虚部翻转而已：
z＝a+bi
它的复数共轭就是：
z* ＝a-bi
注意，b不一定是要“负的”。如果z＝3-4i，那么z* ＝3+4i。
6.7 乘以复数的共轭
如果乘以一个复数乘以它的共轭会发生什么呢？z乘以z* 等于多少呢？看看这个：
z·z* ＝1·z·z*
所以我们选择一个1（一个实数），加上z的角度，再加上z* 的角度。但是最后一个角度是负的——是个减法！所以我们最终的结果就是一个实数，因为我们把角度消掉了。数字就是|z|2 ，因为我们把大小乘了两次。
现在让我们再做一个例题：(3+4i)(3-4i)=9-16i2 =25
我们得到了一个实数，正如我们所预料的！数学爱好者同样可以试一试这个代数运算：
(a+bi)(a-bi)=a2 +abi-abi+b2i2= a2 + b2
啊哈！最后结果没有虚数部分，而只是大小的平方。我们把复数的共轭认为是一种“反方向旋转”帮助我们预测到了这一结果。
6.8 改变的你的数字
我们乘以一个共轭z* ，就相当于乘以一个|z*|。为了得到相反的效果，我们可以除以|z|，而要再是缩小了|z|我们再除一次即可。总的来说，如果我们乘以一个复共轭那么我们就需要除以|z||z|来保持原数不变。
6.9 向我展示除法！
我之前回避了一些除法，现在是见证奇迹的时刻。如果我们想计算
(3+4i)/(1+i)
我们可以马上得到：
- 旋转一个相反的角度：乘以(1-i)而不是(1+i)
- 除以长度的平方：除以|21/2 |2 =2
答案是：
(3+4i)/(1+i)＝(3+4i)(1-i)(1/2)=(3-4i2 +4i-3i)(1/2)=7/2+(1/2)i
更常见的方法是上下同乘以分母的复共轭。
我们通常只是被告诉“只管上下同乘以它的复共轭”就行了，而从来没能明白其中的原因。今天我们搞明白了。
两种方法都可以（通常使用后一种方法），但是用其中一种检查另外一种也是个不错的主意。
6.10 更多的数学技巧
现在我们既然理解了复共轭，这里有几个关于复共轭的性质：
(x+y)* = x* + y*
(x·y)* = x* · y*
第一个很容易理解，两个数的和再“反射（求共轭）”等价于把它们的共轭相加。另一种理解的办法是：移动两个数然后再取反等价于同时把两个数移动并取反。
第二个性质就比较难理解了。没错，代数运算或许可以，但是更直观的解释是什么呢？（x·y）* 的结果就是：
- 把长度相乘：|x|·|y|
- 把角度相加并取共轭（相反）：角度（x）+角度（y）变为 -角度（x）+ －角度（y）
而x* 乘以y* 就是：
- 长度相乘：|x|·|y|（更上面的相同）
- 共轭角度相加：角度（x*）+角度（y*）＝-角度（x*）+-角度（y*）
- 把角度相加并取共轭（相反）：角度（x）+角度（y）变为 -角度（x）+ －角度（y）
- 共轭角度相加：角度（x*）+角度（y*）＝-角度（x*）+-角度（y*）？？？？？？？？？？
The result (xy)* means:
- Multiply the magnitudes: |x| * |y|
- Add the angles and take the conjugate (opposite): angle(x) + angle(y) becomes “-angle(x) + -angle(y)”
And x* times y* means:
- Multiply the magnitudes: |x| * |y| (this is the same as above)
- Add the conjugate angles: angle(x) + angle(y) = -angle(x) + -angle(y)
啊哈！我们得到了相同的结果，而我们不需要用传统的代数方法。代数方法也可以，但是并不是最让人满意的解释。
6.11 一个简单示例
共轭就是“撤销”一次旋转。试着这样考虑：
- 我存了$3,$10,$15.75,$23.5到我的帐户。什么交易会把这些交易抵消呢？相反的操作：加上它们，然后乘以-1.
- 我通过几次相乘把一套直线做了几次旋转：(3+4i),(1+i),(2+10i)。什么样的操作会把这些旋转抵消呢？相反的操作：乘以这些复数，取它们的复共轭便得到结果。
看到了吧，复共轭就是相当于一种撤销操作，就像负数撤消了相加的效果一样。警告：处理复共轭时，你需要除以|z||z|这样才能抵消它们对大小的影响。
6.12 最后的一些想法
这里的数学并没有什么新的东西，但是我一直没意识到复共轭是怎么发挥作用的。为什么是a-bi而不是-a+bi呢？复共轭并不是一个随意的选择，是从虚数角度考虑的一种镜像，正好就是相反的角度。
看到把虚数看作旋转给了我们一种解决问题的新思路；“乘上再消去”给了我们一种直觉，即使是讨论像复数一样怪异的话题。希望你能享受到快乐的数学。