一、数组的三种创建方式
public static void main(String[] args){
// 1.方式一 声明 分配空间并赋值,静态初始化
int[] arr1 = {1,2,3};
// 2.方式二 显示初始化,动态
int[] arr2;
arr2 =newint[]{1,2,3};
// 3.方式三 显示初始化(),动态
int[] arr3;
arr3 =newint[3];
}
它们的区别
方式一:在声明的时候直接就已经分配空间,并赋值,方式一是不能写成如下这种形式的。
int[] arr1;
arr1 = {1,2,3};//错误写法 编译不同过
方式二和方式三:声明和内存分配是分开的。
二、数组的内存图解
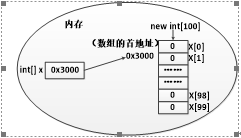
第一行代码 int[] x; 声明了一个变量x,该变量的类型为int[],即一个int类型的数组。变量x会占用一块内存单元,它没有被分配初始值。内存中的状态如下图所示。
第二行代码 x = new int[100]; 创建了一个数组,将数组的地址赋值给变量x。在程序运行期间可以使用变量x来引用数组,这时内存中的状态会发生变化,如下图所示。
在上图中描述了变量x引用数组的情况。该数组中有100个元素,初始值都为0。
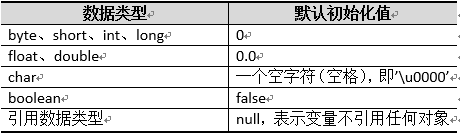
其实数组中根据元素类型的不同,默认初始化的值也是不一样的。具体如下表所示。
三、数组的访问与长度
数组中的每个元素都有一个索引(也可称为角标),要想访问数组中的元素可以通过“x[0]、x[1]、……、x[98]、x[99]”的形式。需要注意的是,数组中最小的索引是0,最大的索引是“数组的长度-1”。
在Java中,为了方便我们获得数组的长度,提供了一个length属性,在程序中可以通过“数组名.length”的方式来获得数组的长度,即元素的个数。
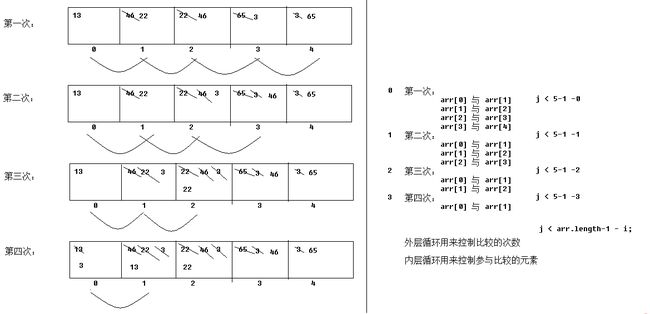
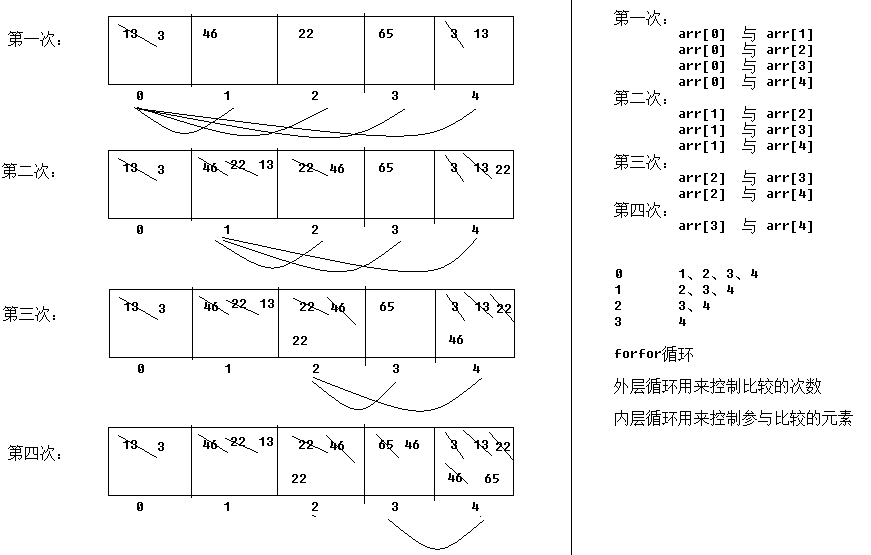
四、数组遍历
在操作数组时,经常需要依次访问数组中的每个元素,这种操作称作数组的遍历。接下来通过一个案例来学习如何使用for循环来遍历数组,如下所示。
public class ArrayDemo04 {
public static voidmain(String[] args) {
int[] arr = { 1, 2,3, 4, 5 };// 定义数组
// 使用for循环遍历数组的元素
for(inti = 0; i < arr.length;i++) {
System.*out*.println(arr[i]);// 通过索引访问元素
}
}
}
五、数组元素的删除
数组的特性是,一旦初始化,则长度确定,所以要删除数组中元素,并且长度也随着删除而改变,则要重新建立数组。
/**
*删除方式1,index为数组需要删除的索引位
*/
public int[] delete(int index, int array[]) {
//数组的删除其实就是覆盖前一位 int[] arrNew = new int[array.length - 1];
for (int i = index; i < array.length - 1; i++) {
array[i] = array[i + 1];
}
System.arraycopy(array, 0, arrNew, 0, arrNew.length);
return arrNew;
}
/**
*删除方式2,index为数组需要删除的索引位
*/
public int[] delete2(int index, int array[]) {
//数组的删除其实就是覆盖前一位 int[] arrNew = new int[array.length - 1];
for (int i = 0; i < array.length - 1; i++) {
if (i < index) {
arrNew[i] = array[i];
} else {
arrNew[i] = array[i + 1];
}
}
return arrNew;
}
六、获取数组最值
在操作数组时,经常需要获取数组中元素的最值。接下来通过一个案例来演示如何获取数组中元素的最大值,如下所示。
publicclassArrayDemo05 {
publicstaticvoidmain(String[] args) {
int[] arr = { 4, 1,6, 3, 9, 8 };// 定义一个数组
intmax = arr[0];//定义变量max用于记住最大数,首先假设第一个元素为最大值
// 下面通过一个for循环遍历数组中的元素
for(intx = 1; x < arr.length;x++) {
if(arr[x] >max) {// 比较arr[x]的值是否大于max
max = arr[x];// 条件成立,将arr[x]的值赋给max
}
}
System.*out*.println("max="+ max);//打印最大值
}
}
七、数组异常
1. 数组越界异常ArrayIndexOutOfBoundsException:
每个数组的索引都有一个范围,即0~length-1。在访问数组的元素时,索引不能超出这个范围,否则程序会报错。
int[] arr ={11,22};
System.out.println( arr[2] );//会产生数组越界异常
2. 空指针异常NullPointerException
在使用变量引用一个数组时,变量必须指向一个有效的数组对象,如果该变量的值为null,则意味着没有指向任何数组,此时通过该变量访问数组的元素会出现空指针异常。
int[] arr ={1,2,3};
arr = null;
System.out.println( arr[0] );//会产生空指针异常
八、二维数组
1.二维数组定义格式
第一种方式:
int[][] arr = newint[3][4];
上面的代码相当于定义了一个3*4的二维数组,即二维数组的长度为3,二维数组中的每个元素又是一个长度为4的数组,接下来通过一个图来表示这种情况,如下图所示。
第二种方式:
int[][] arr = newint[3][];
第二种方式和第一种类似,只是数组中每个元素的长度不确定,接下来通过一个图来表示这种情况,如下图所示。
第三种方式:
int[][] arr ={{1,2},{3,4,5,6},{7,8,9}};
上面的二维数组中定义了三个元素,这三个元素都是数组,分别为{1,2}、{3,4,5,6}、{7,8,9},接下来通过一个图来表示这种情况。
2.二维数组元素遍历与数组元素累加和
class ArrayDemo09 {
public static void main(String[] args){
//一维数组的求累加和并遍历
int[] arr = {10,20,30,40,50};
int sum = 0;
for (int i=0; i
Arrays.png