Codeforces Round 652 Div2

Codeforces Round 652 Div2

Round652的题感觉就是想到了就容易实现，代码不是很复杂。但就这变成了打的最差的一次。。这里记录一下BCD题。

B题 AccurateLee
Lee was cleaning his house for the party when he found a messy string under the carpets. Now he’d like to make it clean accurately and in a stylish way…

The string he found is a binary string of length (i. e. string consists only of 0-s and 1-s).

In one move he can choose two consecutive characters and +1, and if is 1 and +1 is 0, he can erase exactly one of them (he can choose which one to erase but he can’t erase both characters simultaneously). The string shrinks after erasing.

Lee can make an arbitrary number of moves (possibly zero) and he’d like to make the string as clean as possible. He thinks for two different strings and , the shorter string is cleaner, and if they are the same length, then the lexicographically smaller string is cleaner.

Now you should answer test cases: for the -th test case, print the cleanest possible string that Lee can get by doing some number of moves.

Small reminder: if we have two strings and of the same length then is lexicographically smaller than if there is a position such that 1=1, 2=2,…, −1=−1 and <.

Input
The first line contains the integer (1≤≤104) — the number of test cases.

Next 2 lines contain test cases — one per two lines.

The first line of each test case contains the integer (1≤≤105) — the length of the string .

The second line contains the binary string . The string is a string of length which consists only of zeroes and ones.

It’s guaranteed that sum of over test cases doesn’t exceed 105.

Output
Print answers — one per test case.

The answer to the -th test case is the cleanest string Lee can get after doing some number of moves (possibly zero).

example input:

5
10
0001111111
4
0101
8
11001101
10
1110000000
1
1

example output:

0001111111
001
01
0
1

简单概括一下：对于一个01串，每次可以删去连续的"10"中的一个0或1，让它变得最短；如果有多个最短，取字典序最小。

开始没思路，想到贪心，每次碰到“10”就怎样怎样处理，但是发现过不了样例。。耽误了好久，才开始思考问题的本质。找规律发现，对于一串数字11…00…1…0…，最后一定可以变换成只有一个数字0或1。所以当时的思路就变成了，先把开头的0过过去，然后找之后最长的1…0…1…0，变成‘0’(字典序最小)。所以当时ac的代码是这样的：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
int t,n;
int main()
{
    cin>>t;
    while(t--){
        cin>>n;
        string s;
        cin>>s;
        string res="";
        int i=0;
        while(i<s.size()&&s[i]=='0'){
            res.push_back('0');
            i++;
        }
        int flag=0;
        while(i<s.size()){
            int j=i;
            while(j<s.size()&&s[j]=='1') j++;
            if(j==s.size()){
                if(flag) res=res+"0"+s.substr(i,s.size()-i);
                else res=res+s.substr(i,s.size()-i);
                break;
            }
            else{
                while(j<s.size()&&s[j]=='0') {flag=1;j++;}
                i=j;
                if(j==s.size()){
                    res=res+"0";
                }
            }
        }
        cout<<res<<endl;
    }
    return 0;
}

但其实换个思路来讲，其实就是要把最长的1…0…1…0…变成’0’，完全可以间接找到，也就是说，从开头走过所有的0，从结尾往头走过所有的1，剩下的不就是最长的1…0…1…0…串了吗。。哎太蠢了。。所以正常的写法如下：

#include 
int main() {
    int t;
    std::cin >> t;
    while (t--) {
        int n;
        std::cin >> n;
        std::string s;
        std::cin >> s;
        int i = 0, j = n;
        while (i < n && s[i] == '0')
            ++i;
        while (j > 0 && s[j - 1] == '1')
            --j;
        if (i == j) {
            std::cout << s << "\n";
        } else {
            std::cout << s.substr(0, i) + '0' + s.substr(j) << "\n";
        }
    }
    return 0;
}

C题 RationalLee
Lee just became Master in Codeforces, and so, he went out to buy some gifts for his friends. He bought integers, now it’s time to distribute them between his friends rationally…

Lee has integers 1,2,…, in his backpack and he has friends. Lee would like to distribute all integers in his backpack between his friends, such that the -th friend will get exactly integers and each integer will be handed over to exactly one friend.

Let’s define the happiness of a friend as the sum of the maximum and the minimum integer he’ll get.

Lee would like to make his friends as happy as possible, in other words, he’d like to maximize the sum of friends’ happiness. Now he asks you to calculate the maximum sum of friends’ happiness.

Input
The first line contains one integer (1≤≤104) — the number of test cases.

Next 3 lines contain test cases — one per three lines.

The first line of each test case contains two integers and (1≤≤2⋅105; 1≤≤) — the number of integers Lee has and the number of Lee’s friends.

The second line of each test case contains integers 1,2,…, (−109≤≤109) — the integers Lee has.

The third line contains integers 1,2,…, (1≤≤; 1+2+…+=) — the number of integers Lee wants to give to each friend.

It’s guaranteed that the sum of over test cases is less than or equal to 2⋅105.

Output
For each test case, print a single integer — the maximum sum of happiness Lee can achieve.

example input:

3
4 2
1 13 7 17
1 3
6 2
10 10 10 10 11 11
3 3
4 4
1000000000 1000000000 1000000000 1000000000
1 1 1 1

example output

48
42
8000000000

简单概括一下：n个数，分成k个组，第i个组大小是w[i]，要使得每个组最大值+最小值的和最大。（只有一个元素的组最大值最小值都是本身）。

这个题第一眼看上去也没什么思路。。但是仔细想想，要尽可能让最大的几个值都在里面出现，然后最小的值尽量都凑到一个组里去，这样每个组的最小值会变大。所以就产生一种贪心策略：排序，然后每个组放一个最大的，然后把最小的从数量最大的组开始放。但放最大的有个问题，最大的元素要优先放在只有一个元素的组，因为这样最小值也会计算到这个大的数，就赚了。严谨的证明还是比较烦的，可以去看官网。

当时想到这个策略还是挺自然的，结果第一遍写的时候写了个bug，WA了，就以为是不可贪心的了。。又想不到其他办法，卡了半天，结果换了个方式重写了一遍就过了，也算是舒服了。。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
int t,n,k;
int a[200010],w[200010];
int main()
{
    cin>>t;
    while(t--){
        cin>>n>>k;
        for(int i=0;i<n;i++) cin>>a[i];
        for(int i=0;i<k;i++) cin>>w[i];
        sort(a,a+n);
        sort(w,w+k,greater<int>());
        long long res=0;
        int aindex=n-1,windex=k-1;
        for(;windex>=0&&w[windex]==1;windex--){
            res+=2*a[aindex];
            aindex--;
        }
        for(int i=0;i<windex+1;i++){
            res+=a[aindex--];
        }
        aindex=0;
        for(int i=0;i<windex+1;i++){
            res+=a[aindex];
            aindex+=(w[i]-1);
        }
        cout<<res<<endl;
    }
    return 0;
}

D题 TediousLee
Lee tried so hard to make a good div.2 D problem to balance his recent contest, but it still doesn’t feel good at all. Lee invented it so tediously slow that he managed to develop a phobia about div.2 D problem setting instead. And now he is hiding behind the bushes…

Let’s define a Rooted Dead Bush (RDB) of level as a rooted tree constructed as described below.

A rooted dead bush of level 1 is a single vertex. To construct an RDB of level we, at first, construct an RDB of level −1, then for each vertex :

• if has no children then we will add a single child to it;
• if has one child then we will add two children to it;
• if has more than one child, then we will skip it.

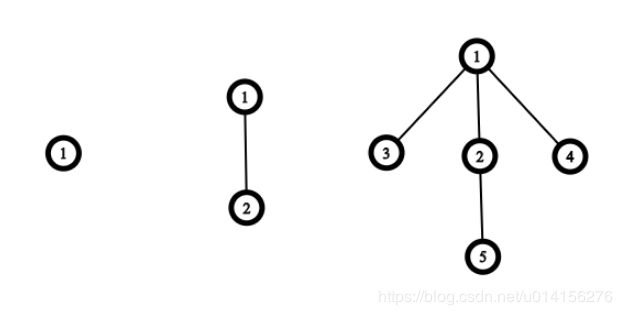
Let’s define a claw as a rooted tree with four vertices: one root vertex (called also as center) with three children. It looks like a claw:

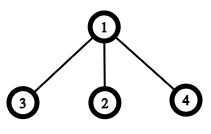
Lee has a Rooted Dead Bush of level . Initially, all vertices of his RDB are green.

In one move, he can choose a claw in his RDB, if all vertices in the claw are green and all vertices of the claw are children of its center, then he colors the claw’s vertices in yellow.

He’d like to know the maximum number of yellow vertices he can achieve. Since the answer might be very large, print it modulo 109+7.

Input
The first line contains one integer (1≤≤104) — the number of test cases.

Next lines contain test cases — one per line.

The first line of each test case contains one integer (1≤≤2⋅106) — the level of Lee’s RDB.

Output
For each test case, print a single integer — the maximum number of yellow vertices Lee can make modulo 109+7.

example input

7
1
2
3
4
5
100
2000000

example output

0
0
4
4
12
990998587
804665184

这题容易想到dp，因为每个节点之后的历程都是一样的。更进一步可以发现，对于level i的树，中间下面是level i-1的树，左右挂着的是level i-2的树。所以容易想到dp[i]=dp[i-1]+2*dp[i-2]。

但是还要注意，因为level i的树的根节点和三个子树的根节点又可以形成一个claw，这个claw能不能取，还要看情况。如果三个子树的根都没用于形成claw，那么就可以形成一个新claw。可以看到i=3时形成了一个新的claw，用到了根节点，i=4的根节点就是空闲的，i=5根节点也是空闲的，到了i=6，根部就又可以形成一个新claw，而且根节点就不空了。下一次形成新claw就要等到i=9。所以dp[i]=dp[i-1]+2dp[i-2]+4(i%3==0)。代码如下：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
int t,n,k;
long long dp[2000010];
int main()
{
    dp[1]=0;
    dp[2]=0;
    for(int i=3;i<=2000000;i++){
        dp[i]=(2*dp[i-2]+dp[i-1]+4*(i%3==0))%(1000000007);
    }
    cin>>t;
    while(t--){
        int x;
        cin>>x;
        cout<<dp[x]<<endl;
    }
    return 0;
}