迷宫求解【穷举求解法】
迷宫求解是一个理解数据结构中栈的比较好的实践例子,下面进行分析
设迷宫是又一个2维数组组成的,元素只有0或1来表示是否通路,0代表通路,1代表有墙壁不通路
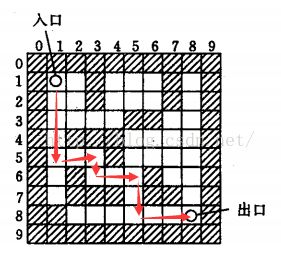
例如下图中是一条通路
穷举法:从入口出发,顺某方向向前探索,如能走通,则继续往前走,否则沿原路返回,换一个方向再试,直到所有可能的铜锣都探索到为止。为了保证在任何时候都有可能沿原路返回,所有要用后进先出的结构---栈来保存从入口到当前位置的路径。
当前位置是指在搜索过程中某时刻所在图中某方块的位置。若当前位置“可通”,则纳入“当前路径”,并继续朝下一个位置搜索,即切换下一个位置为当前位置,如此重复直至到达出口;若当前位置不可通,则退会到前一个通块,在这个通块的其他方向再次前进尝试,若该通道块的4个方向都不可通,则从当前路径上删除该通道块,再尝试前一个通道块,以此类推。
当前路径的最上面的一个通道块是当前路径栈中的栈顶,纳入路径相当于入栈,删除或退后就相当于出栈。
算法的描述
do{
若当前位置可通
则{将当前位置插入栈顶
若当前位置是出口位置,则结束
否则切换当前位置的东邻方块为新的当前位置
}
否则{
若栈不空且栈顶位置尚有其他方向未经搜索
则设定新的当前位置为沿顺时针方向旋转找到的栈顶位置的下一相邻块
若栈不空但栈顶位置的四周都不通
则{ 删去栈顶位置
若栈不空,则重新测试新的栈顶位置
直到找到一个可通的相邻块或出栈至栈空
}
}
}while(栈不空)
为了方便,我们先前要定义好迷宫的数据,例如
int R[10][10]={
{0,0,1,0,0,0,0,1,0,1},
{1,0,1,0,1,1,0,1,1,0},
{1,0,0,0,1,1,0,0,0,1},
{0,1,0,1,1,0,0,1,1,1},
{0,1,0,0,1,1,0,1,0,0},
{1,0,1,0,1,1,0,0,1,0},
{0,1,1,0,0,0,1,0,1,1},
{0,1,0,1,1,0,0,0,0,0},
{0,1,1,0,0,1,1,1,1,0},
{1,0,1,0,1,1,0,0,1,0}};在此需要用到的数据为
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int DirectiveType;
typedef int Status;
typedef struct{
int row;
int col;
}PosType;//通道块类型,代表的坐标(行,列)
typedef struct{
int step;//在路径中的序号
PosType seat;//位置坐标
DirectiveType di;//方向 1代表东 2代表南 3代表西 4 代表北
}SElemType;//栈元素类型,
typedef struct{
SElemType *base;//栈底
SElemType *top;//栈顶
int stacksize;//栈的尺寸大小
}SqStack;//栈的类型,栈的一些基本操作
#define STACK_INIT_SIZE 100//初始栈的大小
#define STACKINCREMENT 10//每次栈补充的大小
Status InitStack(SqStack &S)
{
S.base=(SElemType*)malloc(sizeof(SElemType)*STACK_INIT_SIZE);
if(!S.base) exit(OVERFLOW);
S.top=S.base;
S.stacksize=STACK_INIT_SIZE;
return OK;
}
Status GetTop(SqStack S,SElemType &e)
{
if(S.base == S.top) return ERROR;
e=*(S.top-1);
return OK;
}
Status Push(SqStack &S,SElemType e)
{
if(S.top-S.base >= S.stacksize)
{
S.base=(SElemType *)realloc(S.base,(S.stacksize+STACKINCREMENT)*sizeof(SElemType));
if(!S.base) exit(OVERFLOW);
S.top=S.base+S.stacksize;
S.stacksize+=STACKINCREMENT;
}
*S.top++ = e;
return OK;
}
Status Pop(SqStack &S,SElemType &e)
{
if(S.top == S.base) return ERROR;
e = * --S.top;
return OK;
}
Status StackEmpty(SqStack S)
{
return S.base == S.top;
}#define ROW 10
#define COL 10
#define RANGE 100
typedef struct {
int m,n;
int arr[RANGE][RANGE];
}MazeType;
Status InitMaze(MazeType &Maze,int a[][COL],int row,int col)
{
for(int i=1;i<=row;i++)
{
for(int j=1;j<=col;j++)
Maze.arr[i][j]=a[i-1][j-1];
}
for(int j=0;j<=col+1;j++)
Maze.arr[0][j]=Maze.arr[row+1][j]=1;
for(int i=0;i<= row+1;i++)
Maze.arr[i][0]=Maze.arr[i][col+1]=1;
Maze.m=row;
Maze.n=col;
return OK;
}
Status Pass(MazeType Maze,PosType CurPos)
{
if(Maze.arr[CurPos.row][CurPos.col] == 0)
return 1;
else return 0;
}
Status FootPrint(MazeType &Maze,PosType CurPos)
{
Maze.arr[CurPos.row][CurPos.col]=2;//通的过,留下足迹
return OK;
}
Status MarkPrint(MazeType &Maze,PosType CurPos)
{
Maze.arr[CurPos.row][CurPos.col]=3;//走过但是不能通过
return OK;
}
SElemType CreatSElem(int step,PosType pos,int di)
{
SElemType e;
e.step = step;
e.di = di;
e.seat =pos;
return e;
}
PosType NextPos(PosType CurPos,DirectiveType di)
{
PosType Pos=CurPos;
switch(di)
{
case 1:Pos.col++;break;//East
case 2:Pos.row++;break;//south
case 3:Pos.col--;break;//west
case 4:Pos.row--;break;//north
}
return Pos;
}
Status PosEquare(PosType Pos1,PosType Pos2)
{
if(Pos1.col == Pos2.col && Pos1.row == Pos2.row)
return 1;
else return 0;
}
void PrintMaze(MazeType Maze)
{
int i,j;
printf(" ");
for(i=0;i<=COL+1;i++)
printf("%2d",i);
printf("\n");
for(i=0;i<=ROW+1;i++)
{
printf("%2d",i);
for(j=0;j<=COL+1;j++)
{
switch(Maze.arr[i][j])
{
case 0:printf(" ");break;//没有走过
case 2:printf(" *");break;//走过且走的通
case 3:printf(" @");break;//走过但不通
case 1:printf(" #");break;//障碍
}
}
printf("\n");
}
}
Status MazePath(MazeType &Maze,PosType start,PosType end)
{
SqStack S;
SElemType e;
InitStack(S);
PosType CurPos= start;
int Curstep=1;
do
{
if(Pass(Maze,CurPos))
{
FootPrint(Maze,CurPos);
e=CreatSElem(Curstep,CurPos,1);
Push(S,e);
if(PosEquare(CurPos,end)) return TRUE;
CurPos=NextPos(CurPos,1);
Curstep++;
}
else
{
if(!(StackEmpty(S)))
{
Pop(S,e);
while(e.di == 4 && !StackEmpty(S))
{
MarkPrint(Maze,e.seat);
Pop(S,e);
}
if(e.di<4)
{
e.di++;Push(S,e);
CurPos=NextPos(e.seat,e.di);
}
}
}
}while(!StackEmpty(S));
return FALSE;主函数为
int main()
{
char cmd;int i,j;
PosType start,end;
MazeType Maze;
printf(" ");
for(i=1;i<=COL;i++)
printf("%2d",i);
printf("\n");
for(i=0;i执行结果