血管的三维重建

       问题：断面可用于了解生物组织、器官等的形态。例如，将样本染色后切成厚约1mm的切片，在显微镜下观察该横断面的组织形态结构。如果用切片机连续不断地将样本切成数十、成百的平行切片， 可依次逐片观察。根据拍照并采样得到的平行切片数字图象，运用计算机可重建组织、器官等准确的三维形态。假设某些血管可视为一类特殊的管道，该管道的表面是由球心沿着某一曲线（称为中轴线）的球滚动包络而成。例如圆柱就是这样一种管道，其中轴线为直线，由半径固定的球滚动包络形成。

现有某管道的相继100张平行切片图象，记录了管道与切片的交。图象文件名依次为0.bmp、1.bmp、…、99.bmp，格式均为BMP，宽、高均为512个象素（pixel）。为简化起见，假设：管道中轴线与每张切片有且只有一个交点；球半径固定；切片间距以及图象象素的尺寸均为1。

取坐标系的Z轴垂直于切片，第1张切片为平面Z=0，第100张切片为平面Z=99。Z=z切片图象中象素的坐标依它们在文件中出现的前后次序为

（-256，-256，z），（-256，-255，z），…（-256，255，z），

（-255，-256，z），（-255，-255，z），…（-255，255，z），

……

（ 255，-256，z），（ 255，-255，z），…（255，255，z）。

问题一：请计算管道的中轴线与半径，并给出具体的算法。

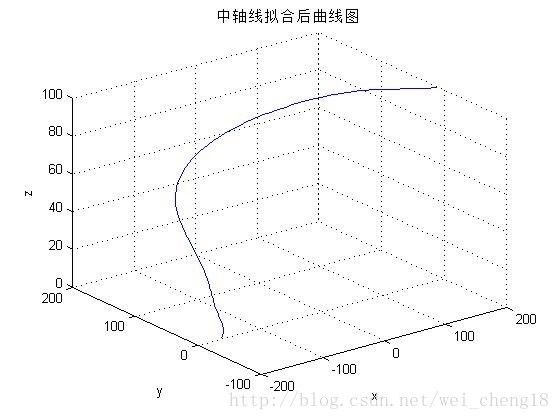
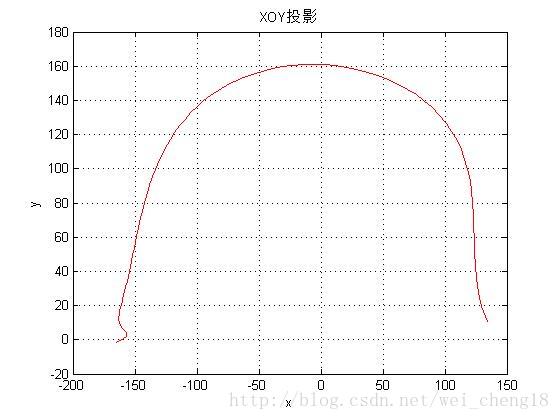
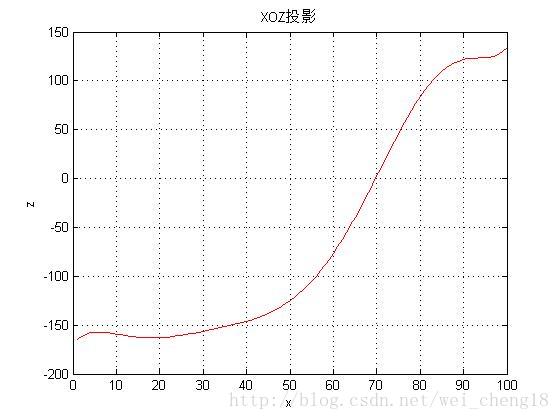
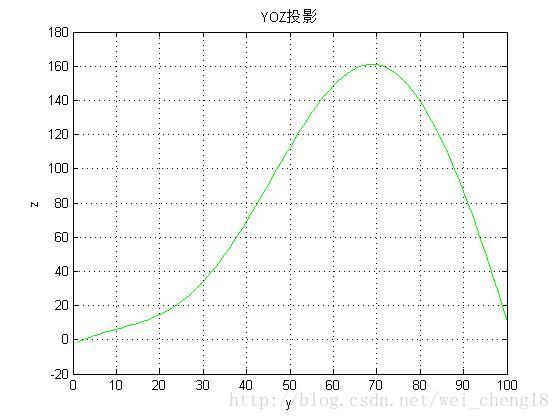
问题二：请绘制中轴线在XY、YZ、ZX平面的投影图。（2001年全国大学生数学建模竞赛题）

        问题分析：分析题目，我们可以知道血管管道是由一组等径的圆球，其圆心按某一曲线(中轴线)滚动所形成的包络.(例如圆柱就是由以直线为中轴线的等径圆球滚动所形成的包络)。每张切面与中轴线有且仅有一个交点，并且这个交点就是切片图像上最大内切圆的圆心，也就是球心的位置。因此，我们的问题一所要求的寻找中轴线与半径，其核心内容就是找图像中最大内切圆的圆心和半径。通过查阅资料我们得知图像轮廓和骨架的定义，寻找最大内切圆的圆心和半径的问题，其解决方案就是求任意一个骨架上的点到所有轮廓点的最小距离，再取所有骨架点对应的最小距离的最大值，此最大值即最大内切圆的半径，对应的点即为最大内切圆的圆心。求出了最大内切圆的半径和球心后，我们可以通过拟合的方式来获取中轴线的图像，同时将最大内切圆的半径取平均值，就可以得到管道的半径。在问题一的基础上，我们求出了最大内切圆的球心和半径，并且通过拟合的方式获得中轴线的图像。这样一来我们可以根据中轴线的图像，使用matlab作图，从而求出中轴线在XY、YZ、ZX平面的投影图。

        按照以上思路，使用matlab软件进行编程，我们可以得到题目中100张切片的最大内切圆圆心坐标及半径，结合体重的信息，中轴线的z轴从1到100，从而得到中轴线在空间中的坐标。

序号	最大内切圆圆心坐标			最大内切圆半径	序号	最大内切圆圆心坐标			最大内切圆半径
	横坐标x	纵坐标y	竖坐标z			横坐标x	纵坐标y	竖坐标z
1	-160	1	1	29.06888	51	-114	117	51	30.41381
2	-160	0	2	28.28427	52	-114	117	52	30.41381
3	-160	1	3	29	53	-113	118	53	30.41381
4	-160	2	4	29.06888	54	-112	119	54	30.41381
5	-160	2	5	29.06888	55	-111	120	55	30
6	-160	2	6	29.06888	56	-111	120	56	29.73214
7	-160	1	7	29	57	-111	120	57	29.69848
8	-160	4	8	29.01724	58	-111	120	58	29.69848
9	-160	1	9	29	59	-81	142	59	29.52965
10	-160	1	10	28.86174	60	-51	156	60	29.54657
11	-160	7	11	28.86174	61	-51	156	61	29.54657
12	-160	8	12	28.86174	62	-31	162	62	29.61419
13	-160	9	13	28.86174	63	-31	162	63	29.61419
14	-160	10	14	29.01724	64	-31	162	64	29.61419
15	-160	12	15	29.01724	65	-35	161	65	29.61419
16	-160	13	16	29.01724	66	-35	161	66	29.61419
17	-160	14	17	29.01724	67	-26	163	67	29.42788
18	-160	16	18	29.01724	68	-35	161	68	29.41088
19	-160	17	19	29.01724	69	-26	163	69	29.27456
20	-160	18	20	29.01724	70	46	163	70	29.42788
21	-160	19	21	29.01724	71	46	163	71	29.61419
22	-160	20	22	29.01724	72	46	163	72	29.61419
23	-160	21	23	29.01724	73	46	163	73	29.61419
24	-160	22	24	29.01724	74	65	158	74	29.61419
25	-160	21	25	29.06888	75	68	157	75	29.73214
26	-160	21	26	29.06888	76	65	158	76	29.73214
27	-160	21	27	29.06888	77	81	152	77	29.54657
28	-159	30	28	29.15476	78	81	152	78	29.52965
29	-159	30	29	29.27456	79	81	152	79	29.52965
30	-159	29	30	29.27456	80	135	117	80	29.69848
31	-158	35	31	29.42788	81	136	116	81	29.69848
32	-157	40	32	29.61419	82	136	116	82	29.69848
33	-157	40	33	29.61419	83	137	115	83	29.69848
34	-157	40	34	29.61419	84	138	114	84	29.69848
35	-156	44	35	29.61419	85	138	114	85	29.69848
36	-153	55	36	29.73214	86	139	113	86	29.69848
37	-153	55	37	29.73214	87	139	113	87	29.69848
38	-153	55	38	29.73214	88	139	113	88	29.69848
39	-152	58	39	29.73214	89	140	112	89	29.69848
40	-152	58	40	29.61419	90	140	112	90	29.69848
41	-150	63	41	29.54657	91	172	67	91	29.52965
42	-135	92	42	29.68164	92	172	67	92	29.52965
43	-148	68	43	29.52965	93	172	67	93	29.52965
44	-119	112	44	29.68164	94	172	67	94	29.52965
45	-118	113	45	29.69848	95	182	43	95	29.73214
46	-117	114	46	29.69848	96	187	24	96	29.61419
47	-117	114	47	29.69848	97	187	24	97	29.61419
48	-116	115	48	30.41381	98	187	24	98	29.61419
49	-115	116	49	30.41381	99	187	24	99	29.61419
50	-115	116	50	30.41381	100	188	18	100	29.42788

在此基础上，使用matlab中的cftool工具箱进行拟合。首先，以x为因变量，z为自变量，得到一个参数方程。同理，以y为因变量，z为自变量，得到一个参数方程。联立上述参数方程，即可得到中轴线的参数方程，在通过matlab中的绘图工具，可以拟合得到中轴线：

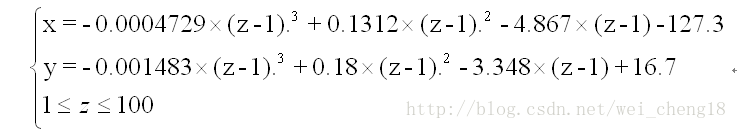
将100个最大内切圆半径求平均值，即可得到管道半径R=29.4924。至此，问题已经得到解决，但我们可以将自己得到的血管管道进行切片，抽样选取其中几个与题目中原有的对比，计算相似度，从而进行检验。

matlab代码如下：

%求圆心半径源代码
jieguo=zeros(100,4);
for k=0:1:99
    A=strcat(int2str(k),'.bmp');
    p0=imread(A);
    for i=1:512
        for j=1:512
            p(i,j)=1-p0(i,j);
        end  
    end
    lunkuo=edge(p,'sobel');%提取轮廓
    gujia=bwmorph(p,'skel',inf);%提取骨架
    [x0,y0,z0]=find(lunkuo);
    [a,b,c]=find(gujia);
    m=length(a);
    n=length(x0);
    r1=zeros(m,n);%骨架和轮廓
    g=zeros(m,2);
    for i=1:m
        for j=1:n
            x1=a(i);
            y1=b(i);
            x2=x0(j);
            y2=y0(j);
            r1(i,j)=sqrt((x1-x2)^2+(y1-y2)^2);
        end
        [r2,zuobiao]=min(r1(i,:));
        g(i,1)=r2;%骨架个数个距离
        g(i,2)=zuobiao;
    end
    [zdr,zdzuobiao]=max(g(:,1));%最大距离
    x=a(zdzuobiao)-256;
    y=b(zdzuobiao)-256;
    
    jieguo(k+1,1)=x;
    jieguo(k+1,2)=y;
    jieguo(k+1,3)=k+1;
    jieguo(k+1,4)=zdr;
    xlswrite('C:\Users\acer\Desktop\新建.xlsx',jieguo);
end

%拟合画中轴线及投影源代码
x = -0.0004729*z.^3 + 0.1312*z.^2 – 4.876*z – 127.3;
y = -0.001483*z.^3 + 0.18*z.^2 - 3.348*z + 16.7;
z=1:100;
figure(1);
plot3(x,y,z);
grid on;
title('中轴线曲线图');
xlabel('x');
ylabel('y');
zlabel('z');

figure(2)
plot(z,x,'r');
grid on;
title('XOZ投影');
xlabel('x');
ylabel('z');

figure(3);
plot(z,y,'g');
grid on;
title('YOZ投影');
xlabel('y');
ylabel('z');

figure(4);
plot(x,y,'r');
grid on;
title('XOY投影');
xlabel('x');
ylabel('y');

%重建后的三维图
for t=0:99
    [x,y,z]=sphere(50);
    x = 5.354e-010*t.^7 -1.783e-007*t.^6 + 2.291e-005*t.^5 - 0.001447*t.^4 + 0.04803*t.^3 - 0.7904*t.^2 + 5.375*t - 169.5 + 29.4924*x;
    y = -7.98e-011*t.^7 + 2.811e-008*t.^6 -3.488e-006*t.^5 + 0.000164*t.^4 -0.001461*t.^3 - 0.02953*t.^2 + 1.2*t -2.719 + 2
9.4924*y;
    z = t + 29.4924*z;
    surf(x,y,z);
    hold on
end
x=xlabel('x');
y=ylabel('y');
z=zlabel('z');
shading interp

%截取重建后模型的切面源代码
R=29.4924;
z=1:100;
x = -0.0004729*(z-1).^3 + 0.1312*(z-1).^2 - 4.867*(z-1) - 127.3;
y = -0.001483*(z-1).^3 + 0.18*(z-1).^2 - 3.348*(z-1) + 16.7;
for m=0:99
a=ones(512,512);
for i=1:512
    for j=1:512
        for p=1:100
            b(p)=sqrt(((i-257)-x(p))^2+((j-257)-y(p))^2+(m+1-p)^2);
        end
        if min(b)<=R
            a(i,j)=0;
        end
    end
end
imwrite(a,strcat('C:\Users\acer\Desktop\第一次\三次\',int2str(m),'.bmp'));
%原图与重建模型切面的相似度百分比
I=imread('C:\Users\dell\Documents\Tencent Files\493976575\FileRecv\第一次\三次\0.bmp'); 
J=imread('0.bmp'); 
[Count1,x]=imhist(I); 
[Count2,x]=imhist(J);
Sum1=sum(Count1);
Sum2=sum(Count2); 
Sumup=sqrt(Count1.*Count2); 
SumDown = sqrt(Sum1*Sum2); 
Sumup = sum(Sumup); 
figure(1);
subplot(2,2,1);
imshow(I); 
subplot(2,2,2);
imshow(J); 
subplot(2,2,3);
imhist(I); 
subplot(2,2,4);
imhist(J);
HistDist=1-sqrt(1-Sumup/SumDown)