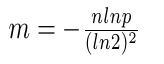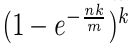题目说明
不安全网页的黑名单包含100亿个黑名单网页,每个网页的URL最多占用64B。现在想要实现一种网页过滤系统,可以根据网页的URL判断该网页是否在黑名单上,请设计该系统。
要求
1. 该系统允许有万分之一以下的判断失误率。
2. 使用的额外空间不要超过30GB。
实现思路
如果把黑名单中所有的URL通过数据库或哈希表保存下来,就可以对每条URL进行查询,但是每个URL有64B,数量是100亿个,所以至少需要640GB的空间,不满足要求2。
如果面试者遇到网页黑名单系统、垃圾邮件过滤系统、爬虫的网址判重系统等题目,又看到系统容忍一定程度的失误率,但是对空间要求比较严格,那么很可能是面试官希望面试者具备布隆过滤器的知识。
设有一个长度为m的bit类型的数组,即数组中的每一个位置只占一个bit,如我们所知,每一个bit只有0和1两种状态。
再假设一共有k个哈希函数,这些函数的输出域S都大于或等于m,并且这些哈希函数都足够优秀,彼此之间也完全独立。那么对同一个输入对象(假设是一个字符串记为URL),经过k个哈希函数算出来的结果也是独立的,可能相同,也可能不同,但彼此独立。对算出来的每一个结果都对m取余(%m),然后在bit array上把相应的位置设置为1。
那么在检查阶段时,如何检查某一个对象是否是之前的某一个输入对象呢?假设一个对象为a,想检查它是否是之前的输入对象,就把a通过k个哈希函数算出k个值,然后把k个值取余(%m),就得到在[0,m-1]范围上的k个值。接下来在bitMap上看这些位置是不是都为1。如果有一个不为1,说明a一定不在这个集合里。
如何计算布隆过滤器大小以及判断失误率
黑名单中样本的个数为100亿个,记为n;失误率不能超过0.01%,记为p;每个样本的大小为64B,这个信息不会影响布隆过滤器的大小,只和选择哈希函数有关,一般的哈希函数都可以接收64B的输入对象,所以使用布隆过滤器还有一个好处是不用顾忌单个样本的大小,它丝毫不能影响布隆过滤器的大小。
所以n=100亿,p=0.01%,布隆过滤器的大小m由以下公式确定:
根据公式计算出m=19.19n,向上取整为20n,即需要2000亿个bit,也就是25GB。
哈希函数的个数由以下公式决定:
计算出哈希函数的个数为k=14个。
然后用25GB的bitMap再单独实现14个哈希函数,根据如上描述生成布隆过滤器即可。
因为我们在确定布隆过滤器大小的过程中选择了向上取整,所以还要用如下公式确定布隆过滤器真实的失误率为:
根据这个公式算出真实的失误率为0.006%,这是比0.01%更低的失误率,哈希函数本身不占用什么空间,所以使用的空间就是bitMap的大小(即25GB),服务器的内存都可以达到这个级别,所有要求达标。