[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)
接上一篇——视觉初始化的代码和内容的讲解,我们对所有的图像帧(滑动窗口内与外all)提供初始R、T估计,然后进行pnp优化,同时我们也得到了它们对应的IMU坐标系到 l l l系的旋转平移。现在进行视觉惯性联合初始化。
【为什么要用视觉惯性联合初始化?怎样联合?】
对于单目系统:
- 视觉系统只能获得二维信息,损失了一维信息(深度)——>利用三角化重新获得损失的深度信息;
- 相机之间是非米制单位表示(s尺度因子),IMU与相机之间是米制单位,需要将其统一——>用IMU来标定这个尺度——>利用IMU预积分,得到PVQ的P;
- IMU存在bias,视觉获得的旋转矩阵不存在bias——>用视觉来标定IMU的旋转bias;
- 世界坐标系这个先验信息的确定?——>通过初始化能借助g来确定;
对于双目系统:
双目可以确定深度,只需要通过g的方向(先验)来确定世界坐标系。
【注意】这个初始化只进行一次就够了,大部分时候,系统都处于NON_LINEAR的状态。因为,一次初始化后,就能确定尺度scaler和bias初始值,scaler确定后,在初始化获得的这些路标点都准确,后续通过PnP或者BA得到的特征点都是真实尺度。但bias初始值确定以后,在后续的非线性优化过程中,会实时更新。
initialStructure()主要代码:
bool Estimator::initialStructure()
{
TicToc t_sfm;
//1.1 通过滑窗内所有帧的线加速度的标准差判断IMU的运动情况 check imu observibility
...
var = sqrt(var / ((int)all_image_frame.size() - 1));
if (var < 0.25)
{
// ROS_INFO("IMU excitation not enouth!");
//return false;
}
...
// 1.2 更新sfm_f 将f_manager.feature中的feature存储到sfm_f中
for (auto &it_per_id : f_manager.feature) // 遍历滑窗中出现的所有特征点
{ ...
{
tmp_feature.observation.push_back(make_pair(imu_j, Eigen::Vector2d{pts_j.x(), pts_j.y()}));
}
sfm_f.push_back(tmp_feature);
}
// 1.3 求解最新帧和滑动窗口中第一个满足条件的帧之间的位姿关系
....
if (!relativePose(relative_R, relative_T, l))
{
cout << "Not enough features or parallax; Move device around" << endl;
return false;
}
// 1.4 对窗口中每个图像帧求解sfm问题
GlobalSFM sfm;
if (!sfm.construct(frame_count + 1, Q, T, l, relative_R, relative_T,
sfm_f, sfm_tracked_points))
{
// SFM重建失败
cout << "global SFM failed!" << endl;
marginalization_flag = MARGIN_OLD; // 边缘化标志设置
return false; // 初始化失败
}
// 1.5 solve pnp for all frame
...
if (!cv::solvePnP(pts_3_vector, pts_2_vector, K, D, rvec, t, 1)) // 输出帧间的变换rvec, t
{
cout << " solve pnp fail!" << endl;
return false;
}
...
// 1.6 视觉惯性联合优化
if (visualInitialAlign())
return true;
else
{
cout << "misalign visual structure with IMU" << endl;
return false;
}
}
由于视觉惯性联合优化的代码也比较多,这里我们先分析视觉和IMU对齐部分。
要完成的部分是:
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第2张图片](http://img.e-com-net.com/image/info8/012f62556a2d46a9b5b183f02f35e815.jpg)
关于VisualIMUAlignment这部分的视觉和IMU对齐初始化的流程图:
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第3张图片](http://img.e-com-net.com/image/info8/a1d6ef0102524a7a9c1a11b2dcd7185f.jpg)
下面对VisualIMUAlignment的代码进行分析。以下内容对应上一篇博客的1.6部分。
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第4张图片](http://img.e-com-net.com/image/info8/2b21fb51d6fe4dc291fd36f6a4ad9137.jpg)
VisualIMUAlignment函数分析
- 1. 计算陀螺仪偏置,尺度,重力加速度和速度
- 1.1 利用相机旋转约束标定IMU角速度bias:solveGyroscopeBias()
- 1.1.1 理论
- 1.1.2 代码
- 1.2 利用IMU的平移约束估计重力方向/各 b k b_k bk帧速度/尺度scaler
- 1.2.1 理论
- 1.2.2 代码
- 1.3 利用 g w g_w gw的模长已知这个先验条件进一步优化 g c 0 g_{c_0} gc0
- 1.3.1 理论
- 1.3.2 代码
- 2. 视觉SFM运动和IMU预积分结果对齐后位姿的计算
- 相机坐标系对齐世界坐标系
1. 计算陀螺仪偏置,尺度,重力加速度和速度
bool Estimator::visualInitialAlign()
{
TicToc t_g; // 时间
VectorXd x;
//solve scale
bool result = VisualIMUAlignment(all_image_frame, Bgs, g, x);
if (!result)
{
//ROS_DEBUG("solve g failed!");
return false;
}
...
}实现函数在VisualIMUAlignment(all_image_frame, Bgs, g, x);实现视觉和IMU的对齐。
bool VisualIMUAlignment(map<double, ImageFrame> &all_image_frame, Vector3d *Bgs, Vector3d &g, VectorXd &x);进去VisualIMUAlignment()函数,此代码在initial_alignment.cpp;
bool VisualIMUAlignment(map<double, ImageFrame> &all_image_frame, Vector3d* Bgs, Vector3d &g, VectorXd &x)
{
// 利用相机旋转约束标定IMU角速度bias
solveGyroscopeBias(all_image_frame, Bgs);
// 利用IMU的平移约束估计重力方向/各b_k帧速度/尺度scaler
if(LinearAlignment(all_image_frame, g, x))
return true;
else
return false;
}
现在,分别分析solveGyroscopeBias()和LinearAlignment()函数。
1.1 利用相机旋转约束标定IMU角速度bias:solveGyroscopeBias()
1.1.1 理论
外参数 q b c q_{bc} qbc标定好后,可以利用旋转约束,可估计陀螺仪 bias:
![]()
有下式:
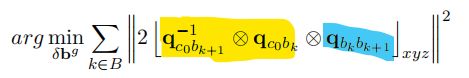
其中,B 表示所有的图像关键帧集合。在SfM完成且外参数标定完之后,公式中黄色部分已知(假设很准)。蓝色部分是IMU预积分得到的,而预积分里面有bias,所以,通过最小化这个目标函数,可以把旋转bias标定出来。
q b k b k + 1 q_{b_kb_{k+1}} qbkbk+1 = q c 0 b k − 1 ⨂ q c 0 b k + 1 ⨂ q^{-1}_{c_0b_{k}}\bigotimes{q_{c_0b_{k+1}}}\bigotimes{} qc0bk−1⨂qc0bk+1⨂ [ 1 0 ] \left[ \begin{matrix} 1 \\ 0 \end{matrix} \right] [10]
代入bias残差后可得:
q ^ b k b k + 1 ⨂ \hat{q}_{b_kb_{k+1}}\bigotimes{} q^bkbk+1⨂ [ 1 1 2 J b g q δ b g ] \left[ \begin{matrix} 1 \\ \frac{1}{2}J^q_{b^g}\delta{b^g} \end{matrix} \right] [121Jbgqδbg] = q c 0 b k − 1 ⨂ q c 0 b k + 1 ⨂ q^{-1}_{c_0b_{k}}\bigotimes{q_{c_0b_{k+1}}}\bigotimes{} qc0bk−1⨂qc0bk+1⨂ [ 1 0 ] \left[ \begin{matrix} 1 \\ 0 \end{matrix} \right] [10]
实部没有需要标定的量,所以只用考虑虚部,可以得到:
J b g q δ b g J^q_{b^g}\delta{b^g} Jbgqδbg = 2 ( q ^ b k b k + 1 − 1 ⨂ 2(\hat{q}^{-1}_{b_kb_{k+1}}\bigotimes{} 2(q^bkbk+1−1⨂ q c 0 b k − 1 ⨂ q c 0 b k + 1 ) q^{-1}_{c_0b_{k}}\bigotimes{q_{c_0b_{k+1}}}) qc0bk−1⨂qc0bk+1)
等式两边同时乘以 J b g q T {J^q_{b^g}}^T JbgqT,可以构造出 A δ b g = B A\delta{b^g}=B Aδbg=B正定方程的形式,在采用LDLT分解,就可以求出状态量 δ b g \delta{b^g} δbg:
J b g q T {J^q_{b^g}}^T JbgqT J b g q δ b g J^q_{b^g}\delta{b^g} Jbgqδbg = 2 J b g q T {J^q_{b^g}}^T JbgqT ( q ^ b k b k + 1 − 1 ⨂ (\hat{q}^{-1}_{b_kb_{k+1}}\bigotimes{} (q^bkbk+1−1⨂ q c 0 b k − 1 ⨂ q c 0 b k + 1 ) q^{-1}_{c_0b_{k}}\bigotimes{q_{c_0b_{k+1}}}) qc0bk−1⨂qc0bk+1)
1.1.2 代码
【代码】
此公式 A δ b g = B A\delta{b^g}=B Aδbg=B的内容与代码完全对应,代码的解析已经在代码中的注释中表明:
void solveGyroscopeBias(map<double, ImageFrame> &all_image_frame, Vector3d* Bgs)
{
// 1.参数的传入和容器的定义
// 传入的参数是all_image_frame
// frame_i和frame_j分别读取all_image_frame中的相邻两帧
Matrix3d A;
Vector3d b;
Vector3d delta_bg;
A.setZero();
b.setZero();
map<double, ImageFrame>::iterator frame_i;
map<double, ImageFrame>::iterator frame_j;
// 2. 构造Ax=b等式
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++)
{
frame_j = next(frame_i);
MatrixXd tmp_A(3, 3);
tmp_A.setZero();
VectorXd tmp_b(3);
tmp_b.setZero();
// 得到相邻两帧的旋转四元数:q_ij
Eigen::Quaterniond q_ij(frame_i->second.R.transpose() * frame_j->second.R); // 运算中的R都是相对于l帧的
// q相对于陀螺仪bias的雅可比
tmp_A = frame_j->second.pre_integration->jacobian.template block<3, 3>(O_R, O_BG);
tmp_b = 2 * (frame_j->second.pre_integration->delta_q.inverse() * q_ij).vec();
A += tmp_A.transpose() * tmp_A;
b += tmp_A.transpose() * tmp_b;
}
// 3.ldlt分解
delta_bg = A.ldlt().solve(b);
// ROS_WARN_STREAM("gyroscope bias initial calibration " << delta_bg.transpose());
// 4. 给滑窗内的IMU预积分加入角速度bias
for (int i = 0; i <= WINDOW_SIZE; i++)
Bgs[i] += delta_bg;
// 5.重新计算所有帧的IMU积分(重要!)
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end( ); frame_i++)
{
frame_j = next(frame_i);
frame_j->second.pre_integration->repropagate(Vector3d::Zero(), Bgs[0]);
}
}其中,repropagate()的预积分重新传播函数,针对的是从 b k b_k bk到 b k + 1 b_{k+1} bk+1的PVQ传播矫正和误差传递矫正。
void repropagate(const Eigen::Vector3d &_linearized_ba, const Eigen::Vector3d &_linearized_bg)
{
sum_dt = 0.0; // the gap between IMU plot
acc_0 = linearized_acc; // a at bk in bk coordinate
gyr_0 = linearized_gyr; // w at bk in bk coordinate
// 预积分
delta_p.setZero(); //alpha
delta_q.setIdentity();
// gama trans bi to bk
delta_v.setZero(); // beta
linearized_ba = _linearized_ba; // a bias
linearized_bg = _linearized_bg; // w bias
jacobian.setIdentity();
covariance.setZero();
for (int i = 0; i < static_cast<int>(dt_buf.size()); i++)
propagate(dt_buf[i], acc_buf[i], gyr_buf[i]);
}其中,propagate()传播函数,针对的是 b k b_k bk和 b k + 1 b_{k+1} bk+1内部的 i i i时刻到 i + 1 i+1 i+1时刻的PVQ传播和误差传递。
// 传播函数,针对的是bk和bk+1内部的i时刻到i+1时刻的PVQ传播和误差传递。
void propagate(double _dt, const Eigen::Vector3d &_acc_1, const Eigen::Vector3d &_gyr_1)
{
dt = _dt;
acc_1 = _acc_1; // a at time t=t+dt
gyr_1 = _gyr_1; // w at time t=t+dt
Vector3d result_delta_p;
Quaterniond result_delta_q;
Vector3d result_delta_v;
Vector3d result_linearized_ba;
Vector3d result_linearized_bg;
//中值积分法(略)
midPointIntegration(_dt, acc_0, gyr_0, _acc_1, _gyr_1, delta_p, delta_q, delta_v,
linearized_ba, linearized_bg,
result_delta_p, result_delta_q, result_delta_v,
result_linearized_ba, result_linearized_bg, 1);
//checkJacobian(_dt, acc_0, gyr_0, acc_1, gyr_1, delta_p, delta_q, delta_v,
// linearized_ba, linearized_bg);
delta_p = result_delta_p; // alpha_i+1
delta_q = result_delta_q; // gama_i+1 from i+1 coordinate to bk
delta_v = result_delta_v; // beta_i+1
linearized_ba = result_linearized_ba;
linearized_bg = result_linearized_bg;
delta_q.normalize();
sum_dt += dt; // time for bk to bk+1
acc_0 = acc_1; // a_i+1 at bi+1 coordinate
gyr_0 = gyr_1; // w_i+1
}其中, midPointIntegration()中值法预积分的内容和详细代码在我的另一篇博客——指路
1.2 利用IMU的平移约束估计重力方向/各 b k b_k bk帧速度/尺度scaler
需要优化的状态量是各帧在 b k b_k bk坐标系下的速度, c 0 c_0 c0帧下的重力g和SfM的尺度scaler:
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第6张图片](http://img.e-com-net.com/image/info8/80d868ad89a1443ea2157d203a7676ae.jpg)
1.2.1 理论
又 回 头 仔 细 看 了 这 部 分 代 码 , 下 面 所 有 的 c 0 帧 坐 标 系 , 实 际 上 都 是 指 在 滑 动 窗 口 内 与 新 帧 视 差 最 大 的 参 考 帧 c l 帧 , \red{又回头仔细看了这部分代码,下面所有的c_0帧坐标系,实际上都是指在滑动窗口内与新帧视差最大的参考帧c_l帧,} 又回头仔细看了这部分代码,下面所有的c0帧坐标系,实际上都是指在滑动窗口内与新帧视差最大的参考帧cl帧, 所 求 解 出 来 的 重 力 g 也 是 相 对 于 c l 帧 坐 标 系 的 , 最 终 的 相 机 坐 标 系 c 0 与 世 界 坐 标 系 的 对 齐 工 作 , \red{所求解出来的重力g也是相对于c_l帧坐标系的,最终的相机坐标系c_0与世界坐标系的对齐工作,} 所求解出来的重力g也是相对于cl帧坐标系的,最终的相机坐标系c0与世界坐标系的对齐工作, 也 是 先 实 现 c l 帧 坐 标 系 与 世 界 坐 标 系 的 对 齐 , \red{也是先实现c_l帧坐标系与世界坐标系的对齐,} 也是先实现cl帧坐标系与世界坐标系的对齐, 再 实 现 相 机 坐 标 系 c 0 与 世 界 坐 标 系 的 对 齐 . . . 下 面 的 符 号 就 不 改 动 了 \red{再实现相机坐标系c_0与世界坐标系的对齐...下面的符号就不改动了} 再实现相机坐标系c0与世界坐标系的对齐...下面的符号就不改动了
回顾IMU预积分约束:
世界坐标系下:
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第7张图片](http://img.e-com-net.com/image/info8/e91531a869e44010b055129035cfe8c6.jpg)
即,

w坐标系我们不知道,只知道 c 0 c_0 c0坐标系,所以需要把上面的公式转到 c 0 c_0 c0坐标系上,将世界坐标系 w 换成相机初始时刻坐标系 c 0 c_0 c0有:
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第8张图片](http://img.e-com-net.com/image/info8/e7acf7e5b58c42d5b0f8bb9617ebc1e7.jpg)
将上式结合公式(3):
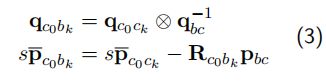
可得:
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第9张图片](http://img.e-com-net.com/image/info8/8c293bdda2f54b7ba33a675d3c615a5d.jpg)
将带估计变量分开,转为 A x = b这种线性方程组的形式:

矩阵的形式即为:

β \beta β也是类似的:
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第10张图片](http://img.e-com-net.com/image/info8/e1ead0343cd24823bd5992de509d59db.jpg)
把这两个矩阵合体,可得:

同样采用LDLT分解,就能求出状态量:
![]()
代码中还加上了信息矩阵,anyway.
1.2.2 代码
LinearAlignment();相关代码的解析都在代码中以注释的方式呈现。
// 利用IMU的平移约束估计重力方向/各b_k帧速度/尺度scalerbool
LinearAlignment(map<double, ImageFrame> &all_image_frame, Vector3d &g, VectorXd &x)
{
// 1. 参数的传入和容器的定义
// 传入的参数是all_image_frame,不仅仅是滑窗内的帧
// frame_i和frame_j分别读取all_image_frame中的相邻两帧
int all_frame_count = all_image_frame.size();
int n_state = all_frame_count * 3 + 3 + 1; // 需要优化的状态量的个数
MatrixXd A{n_state, n_state};
A.setZero();
VectorXd b{n_state};
b.setZero();
map<double, ImageFrame>::iterator frame_i;
map<double, ImageFrame>::iterator frame_j;
// 2. 构造Ax=b等式
int i = 0;
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++, i++)
{
frame_j = next(frame_i);
MatrixXd tmp_A(6, 10);
tmp_A.setZero();
VectorXd tmp_b(6);
tmp_b.setZero();
double dt = frame_j->second.pre_integration->sum_dt;
tmp_A.block<3, 3>(0, 0) = -dt * Matrix3d::Identity();
tmp_A.block<3, 3>(0, 6) = frame_i->second.R.transpose() * dt * dt / 2 * Matrix3d::Identity();
tmp_A.block<3, 1>(0, 9) = frame_i->second.R.transpose() * (frame_j->second.T - frame_i->second.T) / 100.0;
tmp_b.block<3, 1>(0, 0) = frame_j->second.pre_integration->delta_p + frame_i->second.R.transpose() * frame_j->second.R * TIC[0] - TIC[0];
// TIC[0]:p_bc //cout << "delta_p " << frame_j->second.pre_integration->delta_p.transpose() << endl;
tmp_A.block<3, 3>(3, 0) = -Matrix3d::Identity();
tmp_A.block<3, 3>(3, 3) = frame_i->second.R.transpose() * frame_j->second.R;
tmp_A.block<3, 3>(3, 6) = frame_i->second.R.transpose() * dt * Matrix3d::Identity();
tmp_b.block<3, 1>(3, 0) = frame_j->second.pre_integration->delta_v;
//cout << "delta_v " << frame_j->second.pre_integration->delta_v.transpose() << endl;
// 加上了信息矩阵cov_inv
Matrix<double, 6, 6> cov_inv = Matrix<double, 6, 6>::Zero();
//cov.block<6, 6>(0, 0) = IMU_cov[i + 1];
//MatrixXd cov_inv = cov.inverse();
cov_inv.setIdentity();
MatrixXd r_A = tmp_A.transpose() * cov_inv * tmp_A;
VectorXd r_b = tmp_A.transpose() * cov_inv * tmp_b;
// 放入所有帧的A,b;叠加操作
A.block<6, 6>(i * 3, i * 3) += r_A.topLeftCorner<6, 6>();
b.segment<6>(i * 3) += r_b.head<6>();
A.bottomRightCorner<4, 4>() += r_A.bottomRightCorner<4, 4>();
b.tail<4>() += r_b.tail<4>();
A.block<6, 4>(i * 3, n_state - 4) += r_A.topRightCorner<6, 4>();
A.block<4, 6>(n_state - 4, i * 3) += r_A.bottomLeftCorner<4, 6>();
}
A = A * 1000.0; // 免得数据过小???
b = b * 1000.0;
// 3. ldlt分解,得到尺度和g的初始值,并用先验判断
x = A.ldlt().solve(b);
// 从求解出的x向量里边取出最后边的尺度s
double s = x(n_state - 1) / 100.0;
// ROS_DEBUG("estimated scale: %f", s);
// 取出对重力向量g的计算值
g = x.segment<3>(n_state - 4);
// ROS_DEBUG_STREAM(" result g " << g.norm() << " " << g.transpose());
if(fabs(g.norm() - G.norm()) > 1.0 || s < 0)
{
// 如果重力加速度与参考值差太大或者尺度为负则说明计算错误
return false;
}
// !!! 利用gw的模长已知这个先验条件进一步优化gc0(下面接着介绍)
RefineGravity(all_image_frame, g, x);
s = (x.tail<1>())(0) / 100.0;
(x.tail<1>())(0) = s;
// ROS_DEBUG_STREAM(" refine " << g.norm() << " " << g.transpose());
if(s < 0.0 )
return false;
else
return true;
}
【⚠】
/ / 从 求 解 出 的 x 向 量 里 边 取 出 最 后 边 的 尺 度 s \red{ // 从求解出的x向量里边取出最后边的尺度s} //从求解出的x向量里边取出最后边的尺度s
d o u b l e s = x ( n s t a t e − 1 ) / 100.0 ; \red{double s = x(n_state - 1) / 100.0;} doubles=x(nstate−1)/100.0;
1.3 利用 g w g_w gw的模长已知这个先验条件进一步优化 g c 0 g_{c_0} gc0
1.3.1 理论
- 为什么需要优化重力向量?
重力的模长在某一区域内是固定的,而 g c 0 g_{c_0} gc0与其他变量放在一起进行任意优化,不会保证模长限制,比如 ∥ g c 0 ∥ ∥g_{c_0} ∥ ∥gc0∥ = 9.81;而模长的不确定性会影响其他变量的优化结果。
再有,三维变量 g c 0 g_{c_0} gc0实际只有两个自由度,因为它的模长是已知的。
我们采用球面坐标进行参数化,也就是以g的模长为半径画一个半球,上图蓝色线对应的是 g c 0 g_{c_0} gc0的测量值的方向(也就是优化前的方向),在这个交点上找到一个切平面,用 g c 0 g_{c_0} gc0, b 1 b_1 b1, b 2 b_2 b2构造一个坐标系,那么在轴 b 1 b_1 b1和 b 2 b_2 b2上坐标值 w 1 w_1 w1和 w 2 w_2 w2就是我们要求的量,从而得到优化后的 g c 0 g_{c_0} gc0值(方向)。
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第11张图片](http://img.e-com-net.com/image/info8/52892730dacd4f649883fb67453f7a7d.jpg)
三维向量自由度为 2,可以采用球面坐标进行参数化:
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第12张图片](http://img.e-com-net.com/image/info8/b4c9be1e7eba43bdaa4c9e31a1e8b85b.jpg)
b 1 b_1 b1的方向是由 g c 0 g_{c_0} gc0的测量值的方向与[1,0,0]作叉乘得到的, b 2 b_2 b2的方向是由 g c 0 g_{c_0} gc0的测量值的方向与b1作叉乘(与两者都垂直的向量)得到的。
将公式 (19) 代入前面的优化方程, 待优化变量变为:
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第13张图片](http://img.e-com-net.com/image/info8/1d7554a4f0014bb7bf22f099610fe334.jpg)
其中 w c 0 w^{c_0} wc0 = [ w 1 w 2 ] \left[ \begin{matrix} w_1 \\ w_2 \end{matrix} \right] [w1w2];
观测方程b变为:

原AX=b方程即为:

同样使用LDLT分解:
![]()
这一部分做的工作和 1.2 利用IMU的平移估计重力/各bk帧速度/尺度scaler 是相似的,但这是在1.2基础上进一步做的工作。
1.3.2 代码
RefineGravity();相关代码的解析都在代码中以注释的方式呈现。
除了构建切平面空间以及b的表示不同(代公式即可),其他都与上面介绍的1.2一样,参考下前面即可。
// 1.3 利用g_w的模长已知这个先验条件进一步优化g_{c_0}
void RefineGravity(map<double, ImageFrame> &all_image_frame, Vector3d &g, VectorXd &x)
{
// (1)参数的传入和容器的定义
// 为g0增加模长限制
Vector3d g0 = g.normalized() * G.norm(); // norm():范数,g的模长
Vector3d lx, ly;
//VectorXd x;
int all_frame_count = all_image_frame.size();
int n_state = all_frame_count * 3 + 2 + 1;
MatrixXd A{n_state, n_state};
A.setZero();
VectorXd b{n_state};
b.setZero();
map<double, ImageFrame>::iterator frame_i;
map<double, ImageFrame>::iterator frame_j;
// (2)一共迭代四次求解,并构建切向空间
for(int k = 0; k < 4; k++)
{
MatrixXd lxly(3, 2);
// 切向空间的构建,返回公式中的b1,b2;代码的话放在bc矩阵中
lxly = TangentBasis(g0);
// (3) 构造Ax=b等式
int i = 0;
for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++, i++)
{
frame_j = next(frame_i);
MatrixXd tmp_A(6, 9);
tmp_A.setZero();
VectorXd tmp_b(6);
tmp_b.setZero();
double dt = frame_j->second.pre_integration->sum_dt;
tmp_A.block<3, 3>(0, 0) = -dt * Matrix3d::Identity();
tmp_A.block<3, 2>(0, 6) = frame_i->second.R.transpose() * dt * dt / 2 * Matrix3d::Identity() * lxly;
tmp_A.block<3, 1>(0, 8) = frame_i->second.R.transpose() * (frame_j->second.T - frame_i->second.T) / 100.0;
tmp_b.block<3, 1>(0, 0) = frame_j->second.pre_integration->delta_p + frame_i->second.R.transpose() * frame_j->second.R * TIC[0] - TIC[0] - frame_i->second.R.transpose() * dt * dt / 2 * g0; // g0已知
tmp_A.block<3, 3>(3, 0) = -Matrix3d::Identity();
tmp_A.block<3, 3>(3, 3) = frame_i->second.R.transpose() * frame_j->second.R;
tmp_A.block<3, 2>(3, 6) = frame_i->second.R.transpose() * dt * Matrix3d::Identity() * lxly;
tmp_b.block<3, 1>(3, 0) = frame_j->second.pre_integration->delta_v - frame_i->second.R.transpose() * dt * Matrix3d::Identity() * g0;
Matrix<double, 6, 6> cov_inv = Matrix<double, 6, 6>::Zero();
//cov.block<6, 6>(0, 0) = IMU_cov[i + 1];
//MatrixXd cov_inv = cov.inverse();
cov_inv.setIdentity();
MatrixXd r_A = tmp_A.transpose() * cov_inv * tmp_A;
VectorXd r_b = tmp_A.transpose() * cov_inv * tmp_b;
A.block<6, 6>(i * 3, i * 3) += r_A.topLeftCorner<6, 6>();
b.segment<6>(i * 3) += r_b.head<6>();
A.bottomRightCorner<3, 3>() += r_A.bottomRightCorner<3, 3>();
b.tail<3>() += r_b.tail<3>();
A.block<6, 3>(i * 3, n_state - 3) += r_A.topRightCorner<6, 3>();
A.block<3, 6>(n_state - 3, i * 3) += r_A.bottomLeftCorner<3, 6>();
}
A = A * 1000.0;
b = b * 1000.0;
// (4)ldlt分解,得到优化后的状态量x
x = A.ldlt().solve(b);
VectorXd dg = x.segment<2>(n_state - 3);
// 公式(19)的实现
g0 = (g0 + lxly * dg).normalized() * G.norm();
//double s = x(n_state - 1);
}
g = g0;
}注意,代码中 g 0 g_0 g0代表 ∣ ∣ g ∣ ∣ ∗ g ^ c 0 ||g||*\hat{g}_{c_0} ∣∣g∣∣∗g^c0, ∣ ∣ g ∣ ∣ ||g|| ∣∣g∣∣是要代入的模长限制, g ^ c 0 \hat{g}_{c_0} g^c0是1.2部分估算出的g的单位向量(加入模长限制优化前)。
Vector3d g0 = g.normalized() * G.norm();其中,切平面空间的构建TangentBasis(),切空间坐标系b\c的确定完全参照公式(20):
// 切向空间的构建
MatrixXd TangentBasis(Vector3d &g0)
{
Vector3d b, c;
Vector3d a = g0.normalized(); // g0的单位向量
Vector3d tmp(0, 0, 1);
if(a == tmp)
tmp << 1, 0, 0;
b = (tmp - a * (a.transpose() * tmp)).normalized();
c = a.cross(b); // 叉乘
MatrixXd bc(3, 2);
bc.block<3, 1>(0, 0) = b;
bc.block<3, 1>(0, 1) = c;
return bc; // 切平面坐标系
}2. 视觉SFM运动和IMU预积分结果对齐后位姿的计算
至此,VisualIMUAlignment()初始化完成,我们估计得到了陀螺仪bias、有模长限制的重力、各个帧的速度以及尺度初始值。
现在回到visualInitialAlign()视觉惯性联合优化。
在将从视觉SFM中估计出来的位姿信息和IMU预积分的结果对齐之后,我们需要获得世界坐标系中的位姿,也就是计算出PVQ,这样就完成了位姿的初始化估计,后边将用于进行单目紧耦合的VIO操作。
具体包括:
- 获取滑动窗口内所有图像帧相对于第l帧的位姿信息Ps、Rs,并将其置为关键帧
- 重新计算所有f_manager的特征点深度
- 重新计算滑窗内的预积分
- 将 P s 、 V s P_s、V_s Ps、Vs、depth尺度s缩放后从l帧转变为相对于 c 0 c_0 c0帧图像坐标系下
- 利用 g c 0 g_{c_0} gc0和 g w g_w gw确定世界坐标系,也就是实现相机坐标系对齐世界坐标系。
先说一下相机坐标系对齐世界坐标系的理论以及后续的操作,具体代码的解析见下一篇博客。
相机坐标系对齐世界坐标系
对齐流程:
(1) 找到 c 0 c_0 c0到w系的旋转矩阵 R w c 0 = e x p ( [ θ u ] ) R_{wc_0} = exp([θu]) Rwc0=exp([θu])

解释下具体原理:
根据前面的一系列操作, g c 0 g_{c_0} gc0已经求出,而 g w g_w gw一直是已知量,因此它们之间的夹角θ根据公式可求;
然后我们可以用 g c 0 g_{c_0} gc0和 g w g_w gw作叉乘得到一个旋转轴u;
最后把 c 0 c_0 c0坐标系,绕着转轴旋转一个θ,就能找到 c 0 c_0 c0到 w 系的对齐关系,也就是 R w c 0 = e x p ( [ θ u ] ) R_{wc_0} = exp([θu]) Rwc0=exp([θu])。
(2) 把所有 c 0 c_0 c0坐标系下的变量旋转到 w系下
所有量都乘上 R w c 0 R_{wc_0} Rwc0就可以了。我们定义的 c 0 c_0 c0与 w 系的原点坐标是重合的。
(3) 把相机平移和特征点尺度恢复到米制单位
后面的内容在我的另一篇博客——指路
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第1张图片](http://img.e-com-net.com/image/info8/d3713b49503b43d9b052101a845ee815.jpg)
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第5张图片](http://img.e-com-net.com/image/info8/f29fd07c9cea492f946172672af94b48.jpg)
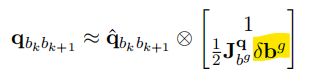
![[从零写VIO|第七节]——VINS-Mono代码精简版代码详解——初始化3视觉IMU对齐(内容|代码)_第14张图片](http://img.e-com-net.com/image/info8/e1f09cb216b647a3a65e805a6baf3ed4.jpg)