java基础--BitMap
BitMap
在一些数据量比较大的场景中,做一些查重、排序,一般的方法难以实现。数据量过大,会占用较大的内存,常用的处理方式有两种:BitMap(位图法)和布隆过滤。
概述
一种大数据外部排序(内存无法加载所有排序元素)、去除重复元素、快速找到随机被删除元素的BitMap小算法,核心思想即通过将一个数作为下标(index)来索引一个bit表示一个数是否存在,排序时的时间复杂度为O(N),需要的额外空间的复杂度O(N/8),
上面的算法都是用一个bit来表示一个数,即只有2种可能,要么有,要么无,可以扩展到一个字节表示一个数,这样就可以统计出现255次范围内的重复元素,原理以此类推。
另外用bit来表示一个int数,节约了31倍的内存空间,即int(4*8),bit(8/1),所以数据量越来使用这种方式的优势越明显,前提是场景适用这种方式。
可以使用bitmap算法,这个很有意思。特别是在数据量大的时候,非常高效
所谓bitmap就是用一个bit位来标记某个元素对应的value,而key即是这个元素。由于采用bit为单位来存储数据,因此在可以大大的节省存储空间。
原理
在java中,一个int类型占32个字节,我们用一个int数组来表示时未new int[32],总计占用内存32*32bit,现假如我们用int字节码的每一位表示一个数字的话,那么32个数字只需要一个int类型所占内存空间大小就够了,这样在大数据量的情况下会节省很多内存。
具体思路:
1个int占4字节即4*8=32位,那么我们只需要申请一个int数组长度为 int tmp[1+N/32]即可存储完这些数据,其中N代表要进行查找的总数,tmp中的每个元素在内存在占32位可以对应表示十进制数0~31,所以可得到BitMap表:
tmp[0]:可表示0~31
tmp[1]:可表示32~63
tmp[2]可表示64~95
.......
那么接下来就看看十进制数如何转换为对应的bit位:
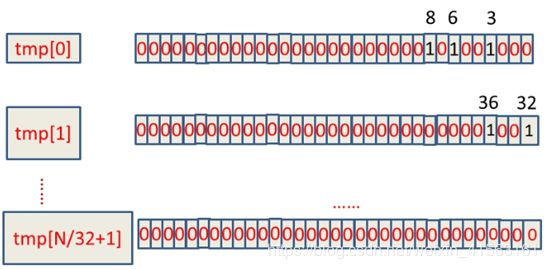
假设这40亿int数据为:6,3,8,32,36,......,那么具体的BitMap表示为:
如何判断int数字在tmp数组的哪个下标,这个其实可以通过直接除以32取整数部分,例如:整数8除以32取整等于0,那么8就在tmp[0]上。另外,我们如何知道了8在tmp[0]中的32个位中的哪个位,这种情况直接mod上32就ok,又如整数8,在tmp[0]中的第8 mod上32等于8,那么整数8就在tmp[0]中的第八个bit位(从右边数起)。
//BitMap源码
public class BitMap2 {
//BitMap源码
private long length;
private static int[] bitsMap;
private static final int[] BIT_VALUE = {0x00000001, 0x00000002, 0x00000004, 0x00000008, 0x00000010, 0x00000020,
0x00000040, 0x00000080, 0x00000100, 0x00000200, 0x00000400, 0x00000800, 0x00001000, 0x00002000, 0x00004000,
0x00008000, 0x00010000, 0x00020000, 0x00040000, 0x00080000, 0x00100000, 0x00200000, 0x00400000, 0x00800000,
0x01000000, 0x02000000, 0x04000000, 0x08000000, 0x10000000, 0x20000000, 0x40000000, 0x80000000};
public BitMap2(long length) {
this.length = length;
/**
* 根据长度算出,所需数组大小
* 当 length%32=0 时大小等于
* = length/32
* 当 length%32>0 时大小等于
* = length/32+l
*/
bitsMap = new int[(int) (length >> 5) + ((length & 31) > 0 ? 1 : 0)];
}
/**
* @param n 要被设置的值为n
*/
public void setN(long n) {
if (n < 0 || n > length) {
throw new IllegalArgumentException("length value "+n+" is illegal!");
}
// 求出该n所在bitMap的下标,等价于"n/5"
int index = (int) n>>5;
// 求出该值的偏移量(求余),等价于"n%31"
int offset = (int) n & 31;
/**
* 等价于
* int bits = bitsMap[index];
* bitsMap[index]=bits| BIT_VALUE[offset];
* 例如,n=3时,设置byte第4个位置为1 (从0开始计数,bitsMap[0]可代表的数为:0~31,从左到右每一个bit位表示一位数)
* bitsMap[0]=00000000 00000000 00000000 00000000 | 00000000 00000000 00000000 00001000=00000000 00000000 00000000 00000000 00001000
* 即: bitsMap[0]= 0 | 0x00000008 = 3
*
* 例如,n=4时,设置byte第5个位置为1
* bitsMap[0]=00000000 00000000 00000000 00001000 | 00000000 00000000 00000000 00010000=00000000 00000000 00000000 00000000 00011000
* 即: bitsMap[0]=3 | 0x00000010 = 12
*/
bitsMap[index] |= BIT_VALUE[offset];
}
/**
* 获取值N是否存在
* @return 1:存在,0:不存在
*/
public int isExist(long n) {
if (n < 0 || n > length) {
throw new IllegalArgumentException("length value illegal!");
}
int index = (int) n>>5;
int offset = (int) n & 31;
int bits = (int) bitsMap[index];
// System.out.println("n="+n+",index="+index+",offset="+offset+",bits="+Integer.toBinaryString(bitsMap[index]));
return ((bits & BIT_VALUE[offset])) >>> offset;
}
}
BitMap应用
- BitMap小小变种:2-BitMap。
看个小场景:在3亿个整数中找出不重复的整数,限制内存不足以容纳3亿个整数。
对于这种场景我可以采用2-BitMap来解决,即为每个整数分配2bit,用不同的0、1组合来标识特殊意思,如00表示此整数没有出现过,01表示出现一次,11表示出现过多次,就可以找出重复的整数了,其需要的内存空间是正常BitMap的2倍,为:3亿*2/8/1024/1024=71.5MB。
具体的过程如下:
扫描着3亿个整数,组BitMap,先查看BitMap中的对应位置,如果00则变成01,是01则变成11,是11则保持不变,当将3亿个整数扫描完之后也就是说整个BitMap已经组装完毕。最后查看BitMap将对应位为11的整数输出即可。
2.已知某个文件内包含一些电话号码,每个号码为8位数字,统计不同号码的个数。
8位最多99 999 999,大概需要99m个bit,大概10几m字节的内存即可。 (可以理解为从0-99 999 999的数字,每个数字对应一个Bit位,所以只需要99M个Bit==1.2MBytes,这样,就用了小小的1.2M左右的内存表示了所有的8位数的电话)
BitMap问题
BitMap 的思想在面试的时候还是可以用来解决不少问题的,然后在很多系统中也都会用到,算是一种不错的解决问题的思路。
但是 BitMap 也有一些局限,因此会有其它一些基于 BitMap 的算法出现来解决这些问题。
- 数据碰撞。比如将字符串映射到 BitMap 的时候会有碰撞的问题,那就可以考虑用 Bloom Filter 来解决,Bloom Filter 使用多个 Hash 函数来减少冲突的概率。
- 数据稀疏。又比如要存入(10,8887983,93452134)这三个数据,我们需要建立一个 99999999 长度的 BitMap ,但是实际上只存了3个数据,这时候就有很大的空间浪费,碰到这种问题的话,可以通过引入 Roaring BitMap 来解决。
实例1
int中32位只能表示一个数,而用BitMap可以表示32一个数:
int[] bitMap:
bitMap[0]:可以表示数字0~31 比如表示0:00000000 00000000 00000000 00000000
比如表示1 : 00000000 00000000 00000000 00000001
bitMap[1]:可以表示数字32~63
bitMap[2]:可以表示数字64~95
……
因此要将一个数插入到bitMap中要进过三个步骤:
1)找到所在bitMap中的index也就是bitMap数组下标
比如我们要在第64一个位置上插入一个数据(也就是插入63)
index = 63 >> 5 = 1,也就是说63应该插入到bitMap[1]中
2)找到63在bitMap[1]中的偏移位置
offset = 63 & 31 = 31说明63在bitMap[1]中32位的最高位
3)将最高位设为1
public class BitMap {
/** 插入数的最大长度,比如100,那么允许插入bitsMap中的最大数为99 */
private long length;
private static int[] bitsMap;
private static final int[] BIT_VALUE = { 0x00000001, 0x00000002, 0x00000004, 0x00000008, 0x00000010, 0x00000020,
0x00000040, 0x00000080, 0x00000100, 0x00000200, 0x00000400, 0x00000800, 0x00001000, 0x00002000, 0x00004000,
0x00008000, 0x00010000, 0x00020000, 0x00040000, 0x00080000, 0x00100000, 0x00200000, 0x00400000, 0x00800000,
0x01000000, 0x02000000, 0x04000000, 0x08000000, 0x10000000, 0x20000000, 0x40000000, 0x80000000 };
public BitMap(long length) {
this.length = length;
// 根据长度算出,所需数组大小
bitsMap = new int[(int) (length >> 5) + ((length & 31) > 0 ? 1 : 0)];
}
/**
* 根据长度获取数据 比如输入63,那么实际上是确定数62是否在bitsMap中
* @return index 数的长度
* @return 1:代表数在其中 0:代表
*/
public int getBit(long index) {
if (index < 0 || index > length) {
throw new IllegalArgumentException("length value illegal!");
}
int intData = (int) bitsMap[(int) ((index - 1) >> 5)];
return ((intData & BIT_VALUE[(int) ((index - 1) & 31)])) >>> ((index - 1) & 31);
}
/**
* @param index
* 要被设置的值为index - 1
*/
public void setBit(long index) {
if (index < 0 || index > length) {
throw new IllegalArgumentException("length value illegal!");
}
// 求出该index - 1所在bitMap的下标
int belowIndex = (int) ((index - 1) >> 5);
// 求出该值的偏移量(求余)
int offset = (int) ((index - 1) & 31);
int inData = bitsMap[belowIndex];
bitsMap[belowIndex] = inData | BIT_VALUE[offset];
}
}
public static void main(String[] args) {
BitMap bitMap = new BitMap(63);
bitMap.setBit(63);
System.out.println(bitMap.getBit(63));
System.out.println(bitMap.getBit(62));
}
实例 2
BitMap 优缺点
优点:实现简单。适合数据量比较大的场景。
缺点:占用内存。申请的数组长度不好控制和最大的数值有关。当某个值特别大的情况下,映射的数组超过申请的数组容量,会出现下标越界。这也是上面提到的10亿个元素占用120M是最小内存的原因,实际可能会大于这个内存。
10亿个正整数,给定一个数值,如何快速排定该数值是否在10亿个正整数当中?
位图法的思想类似于hash寻址,首先初始化一个int数组,每个元素对应32位比特,将10亿个元素分别读入内存,对int数组中的元素比特位进行标记,如果存在,标记为1即可。标记完之后,即可快速判定某个元素是否在10亿个正整数当中,时间复杂度为O(1)。
10亿个元素需要10亿个比特位,10亿/8/1024/1024 = 120 M,相比原来节省了 32 倍内存。
需要申请多大的数组?
array[0]:可表示0~31
array[1]:可表示32~63
array[2]可表示64~95
…
数组长度为10亿/32 +1即可。
1寻址
比如元素 119,如何确定其对应的数组比特位 index ?
1)确定数组 index:119/32 = 3.7,也就是第 4 个数组元素,a[3] 的位置。
2)确定比特位 index:119%32 = 23,第23个比特位。
3)将比特位设置为1。
2设置比特位
1)将比特位设置为1
将第28个比特位设置为1:
只需将 1 左移(31-28)位数,然后与原来的值进行或运算。
2)将比特位设置为0
将第28个比特位设置为0:
只需将 1 左移(31-28)位数,并进行非运算,然后与原来的值进行与运算。
3)判断某一元素是否存在
判断 28 位比特位是否有元素存在:
只需将 1 左移(31-28)位数,然后与原来的值进行与运算。只要与运算结果中有1,即表示元素存在。所以可以用运行结果是不为0作为元素是否存在依据。
public class BigMapTest {
private int[] bigArray;
public BigMapTest(long size){
bigArray = new int[(int) (size/ 32 + 1)];
}
public void set1(int num){
//确定数组 index
int arrayIndex = num >> 5;
//确定bit index
int bitIndex = num & 31;
//设置0
bigArray[arrayIndex] |= 1 << bitIndex;
}
public void set0(int num){
//确定数组 index
int arrayIndex = num >> 5;
//确定bit index
int bitIndex = num & 31;
//设置0
bigArray[arrayIndex] &= ~(1 << bitIndex);
System.out.println(get32BitBinString(bigArray[arrayIndex]));
}
public boolean isExist(int num){
//确定数组 index
int arrayIndex = num >> 5;
//确定bit index
int bitIndex = num & 31;
//判断是否存在
return (bigArray[arrayIndex] & ((1 << bitIndex)))!=0 ? true : false;
}
/**
* 将整型数字转换为二进制字符串,一共32位,不舍弃前面的0
* @param number 整型数字
* @return 二进制字符串
*/
private static String get32BitBinString(int number) {
StringBuilder sBuilder = new StringBuilder();
for (int i = 0; i < 32; i++){
sBuilder.append(number & 1);
number = number >>> 1;
}
return sBuilder.reverse().toString();
}
public static void main(String[] args) {
int[] arrays = new int[]{1, 2, 35, 22, 56, 334, 245, 2234, 54};
BigMapTest bigMapTest = new BigMapTest(2234-1);
for (int i : arrays) {
bigMapTest.set1(i);
}
System.out.println(bigMapTest.isExist(35));
}
}
其它
十进制表示方法,不止一种
ASCII
BCD
压缩BCD
这些都是十进制编码,其中压缩BCD可以多存储一倍的数据
其他,
16Bits 可以表示万进制
32Bits 可以表示亿进制,10 亿进制
这些和十进制优势关系密切的表示方法,转换简单
另外一种 多 字节(字,双字,四字)串 表示方法,
是 二进制表示法,
和十进制转换不太方便,不过+,-,*,/ 等数学运算,实现方便.