吴恩达机器学习笔记(一)(梯度下降)
所以在这里把吴恩达本人写的代码给汉化了,因为网上实在找不到,我不知道他们为什么不这样做,好让我省点力气,希望这篇文章不要被发现很多人发现吧。

如上将介绍最简单的单变量线性函数回归,我们对采集到的一些数据后进行线性拟合。这里称hθ(x)是拟合曲线,上图例子是直线。
蓝线对应着右图的一条等高线,中心点表示拟合程度最高的h(x)。


J(θ0,θ1)叫代价函数,代表拟合程度。如果对代价函数做最小梯度法,去寻找一个θ1,使他能够让代价函数到达最低点,那么hθ(x)也将到达最拟合状态。
关键步骤就是下面这一步,
每次迭代都减去J导数乘以一个学习率。
总结起来就一句话

matlab实现梯度下降法(来源百度百科)
这里的x相当于上图的θ。y相当于代价函数值。步长相当于学习率。
%% 最速下降法图示
% 设置步长为0.1,f_change为改变前后的y值变化,仅设置了一个退出条件。
syms x;
f=x^2;
step=0.1; %设置步长
x=2; %初始值
k=0; %迭代记录数
f_change=x^2; %初始化差值
f_current=x^2; %计算当前函数值
ezplot(@(x,f)f-x.^2); %画出函数图像
axis([-2,2,-0.2,4.1]) %固定坐标轴
hold on
while f_change>0.000000001 %设置条件,两次计算的值之差小于某个数,跳出循环
x=x-step*2*x; %-2*x为梯度反方向,step为步长,!最速下降法!
f_change = f_current - x^2; %计算两次函数值之差
f_current = x^2 ; %重新计算当前的函数值
plot(x,f_current,'ro','markersize',7) %标记当前的位置
drawnow;
pause(0.2);
k=k+1;
end
hold off
fprintf('在迭代%d次后找到函数最小值为%e,对应的x值为%e\n',k,x^2,x)
J的计算公式
J导数的计算公式
代回上式后得
最终的θ计算公式,迭代公式

![]()
matlab代码实现,其中X,y分别代表需要研究的离散的(横坐标值加一列单位列向量,乘上theta就是θ1X+θ0)和(纵坐标),可以自己找到数据后load导入赋值给他们。
梯度下降,计算θ,J
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
m = length(y);
J_history = zeros(num_iters, 1);
for iter = 1:num_iters;
theta = theta - alpha/m * X' *(X*theta - y);
J_history(iter) = computeCost(X, y, theta); %J每一次迭代J的值变动记录,返回可以看到J-history的数值再1500次里不断的梯度下降
end
end
代价函数
function J = computeCost(X, y, theta)
m = length(y);
J = 0; %J初始化
h = X * theta; %h函数定义
J = 1/(2*m) * sum((h-y).^2); %J函数定义
end
主函数
clear ; close all; clc;
data = load('ex1data1.txt'); %自己想研究的离散数据点
X = data(:, 1); y = data(:, 2);
m = length(y); %特征种类个数
plotData(X, y); %画出离散点
X = [ones(m, 1), data(:,1)]; % 我们给X一个单位列向量,乘上theta两个值中的第一个值就是h中的θ0
theta = zeros(2, 1); %初始化theta,是一个长度为2的列向量
iterations = 1500; %迭代次数
alpha = 0.01; %学习率
J = computeCost(X, y, [-1 ; 2]); %调theta的初始值[-1,2],根据具体情况调整
[theta,J_history] = gradientDescent(X, y, theta, alpha, iterations); %将已知量全部带入梯度下降函数
hold on;
plot(X(:,2), X*theta, '-');
legend('Training data', 'Linear regression')
hold off
接main函数,懒得汉化了,实现一些预测的功能和画出J的空间图(xyz分别是θ0 θ1 J)
% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
fprintf('For population = 35,000, we predict a profit of %f\n',...
predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f\n',...
predict2*10000);
%% ============= Part 4: Visualizing J(theta_0, theta_1) =============
% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100); %设定一个范围
theta1_vals = linspace(-1, 4, 100);
% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));% 初始化J_vals
% Fill out J_vals
for i = 1:length(theta0_vals) %ij都100,循环了10000次,所以运行时间在这里被消磨了
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t); %每次循环进去了t是θ0,θ1范围的分段点,返回出来一个J做历史记录
end
end
% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals'; %这里有点没看懂,但事实确实是这样,如果不转置,那么surf出来的表格中底部xy坐标轴会调换,不能体现出真实的J情况。
% Surface plot
figure; %第一张表
surf(theta0_vals, theta1_vals, J_vals);
xlabel('\theta_0');
ylabel('\theta_1');
% Contour plot
figure; %第二张表格
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2); %matlab没有0位置的哈
如果surf之前的循环函数里赋值时,按照正常行→列的顺序则会出现图像bug,要转置
t0 = linspace(-10, 10, 10);
t1 = linspace(-1, 4, 10);
for i = 1:10
for j = 1:10
J(j,i) = t0(i)+t1(j); %如果ij调换则不能体现J的真实情况,可能是根据这个surf的计数顺序有关,surf前两个因为是行向量来计数,最后一个按照列来计数,先第一列从上到下,分别对应t0=-10的时候t1=-1~10的值,然后t0=-8的时候t1=t1=-1~10。然而我们设置循环的时候,是先i后j,如果按照J(i,j),则是以行计数了,那就乱套了。
end
end
surf(t0,t1,J);
其他补充线性代数知识
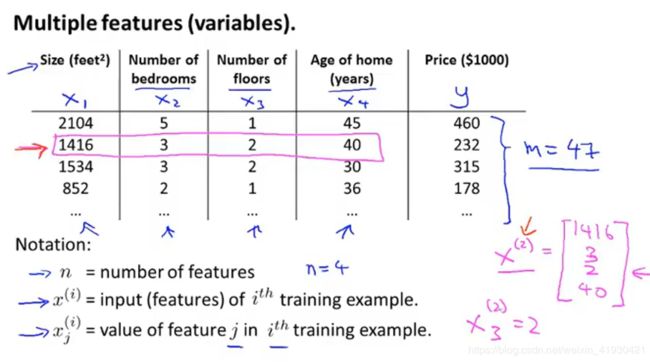
前面我们知道了单变量线性回归的大致思想,现在介绍多变量
我们假定了括号内的数字代表了表格的行数