暴力求解法之子集生成

本文的主要内容是讨论对于特定的集合，如果生成它的所有子集问题，其中涉及到了枚举和递归的思想，我在另一片博文暴力求解法之枚举排列中具体讲解了递归的过程以及解答树相关内容，有兴趣的可以查看。当然，本文也会详细的讨论如何通过枚举和递归来求解子集的问题。

---

1. 增量构造法

增量构造法顾名思义就是逐个增加元素个数来构造子集。下面简单描述利用增量构造法来递归生成子集的过程：

在描述递归过程之前首先应明确两件事情：
①递归终止的条件
②递归函数的参数应该为什么

首先，由于我们是逐个增加元素来构造子集，因此递归终止的条件应为子集的元素达到最大值n，换句话说就是子集元素个数等于集合元素总数。

对于递归函数的参数，我们应该想到的第一个应该是：前一次递归构造得到的子集；此外，原集合可以通过参数传递，也可以作为全局变量。最后，如果利用数组来保存子集，由于无法再函数中判断传入数组的长度，因此我们需要传入当前子集的长度等。（如果利用vector等容器暂存子集则不需要）

伪代码：

void my_subset(已构造序列A， 集合S){
	my_print(A);
	if(终止条件成立) return; //递归终止
	else{
			for(枚举下一个元素){
				my_subset(A加下一个元素, 集合S) // 递归构造
			}
	}
}

其中，在枚举下一个元素时，为了避免出现重复子集，应枚举已构造序列中最后一个元素在集合S中的位置之后的元素，如：
集合S={1, 2, 3, 4, 5}，当前序列A={1, 3}
则应下一轮递归应枚举A={1, 3, 4}、{1, 3, 5}。

n=3时的解答树如下：

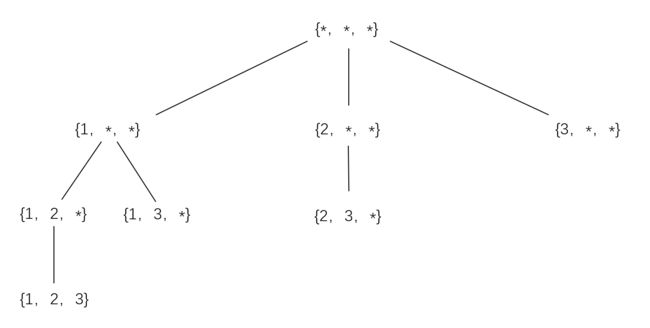
与枚举排列的解答树不同的是，这里所有的结点均为要求的解。因此所有的子集应为：
$$\{\}、\{1\}、\{1,2\}、\{1,2,3\}、\{1,3\}、\{2\}、\{2,3\}、\{3\}$$

示例代码如下：

#include 
#include 
#include 
using namespace std;

void subset(int n, vector<int> vec){
    for(auto i : vec) cout << i;
    cout << endl;
    //if(vec.size() == n) return; //递归终止条件可省略，因为下面不满足循环条件会自动终止
    int start = vec.empty() ? 1 : *(vec.rbegin()) + 1;
    for(int i=start; i<=n; i++){
        vec.push_back(i);
        subset(n, vec);
        vec.pop_back();
    }
}
int main(){
    vector<int> vec;
    subset(3, vec);
    return 0;
}

输出结果为：

1
12
123
13
2
23
3

---

2. 位向量法

位向量法是定义一个长度和集合S相等的数组，每个数取值为0/1（类似于bit），如果集合中的元素对应的"位"取值为0，表示子集不含该元素，如果取值为"1"表示子集包含该元素。例如：S={1, 2, 3}, 则位数组B={0, 1, 0}表示{2}，B={1, 1, 1}表示{1, 2, 3}。

因此，求解子集的问题转换为递归枚举B中的每一个"位"取值为0/1的问题。B的解答树如下图所示：

其中， 树的各层也表示递归的各层，每次递归的时候枚举B中各个位的取值为0或者1，当到达树的叶子结点时，递归结束。因此B的解答树的叶子结点对应着S的每一个子集。所有叶子结点为：
$$\{0,0,0\}、\{0,0,1\}、\{0,1,0\}、\{0,1,1\}、\{1,0,0\}、\{1,0,1\}、\{1,1,0\}、\{1,1,1\}$$
对应S的子集为：
$$\{\}、\{3\}、\{2\}、\{2,3\}、\{1\}、\{1,3\}、\{1,2\}、\{1,2,3\}$$

伪代码：

void my_subset(B, S){
	if(终止条件成立){
		打印结果
		return;
	}else{
		B[下一位]=0; // 枚举
		my_subset(新B， S)  // 递归
		B[下一位]=1; // 枚举
		my_subset(新B， S) // 递归
	}
}

其中，由于B[i]只取0\1，因此不需要使用循环，直接枚举即可。
完整的代码如下：

#include 
#include 
using namespace std;
void my_subset(int n, int *b, int cur){
    if(cur == n){
        for(int i=0; i<cur; ++i){
            if(b[i]) cout << i;
        }
        cout << endl;
        return;
    }
    b[cur]=1;
    my_subset(n, b, cur+1);
    b[cur]=0;
    my_subset(n, b, cur+1);
}
int main(){
    int b[10];
    my_subset(5, b, 0);
    return 0;
}

输出结果如下：

3
2
23
1
13
12
123

---

3. 二进制法

从上面的位向量法可以看到，位向量B的解答树中叶子结点000、001、010、011、100、101、110、111实际上是十进制数$0、1、2、3、4、5、6、7$的二进制表示，也就是说，对于求解集合S的解空间，我们可以用十进制数$0到2^n-1$转换为二进制之后与S中的各个元素作类似于"与"操作的方法。例如：

例：S={1, 2, 3}，则十进制取值为0到7(2^3-1=7)，对应二进制分别为$$000、001、010、011、100、101、110、111$$因此子集为
$$\{\}、\{3\}、\{2\}、\{2,3\}、\{1\}、\{1,3\}、\{1,2\}、\{1,2,3\}$$
更加通用的，假设$S=\{s_1,s_2,...s_n\}$，子集数为$n!$，则十进制数取值为$0\to 2^n-1$，对应二进制数为：
$$\underset{n}{0...00}、\underset{n}{0...01}、\underset{n}{0...10}、...\underset{n}{1...11}$$
然后转换为S的解即可。

可以看到，这种方法可直接枚举，不需要迭代即可求出所有解。

实例代码如下：

#include 
using namespace std;

void my_subset(int n, int s){
    for(int i = 0; i<n; i++){
        if(s&(1<<i)) cout << i+1;
    }
    cout << endl;
}
int main(){
    int n = 3;
    for(int i=0; i<(1<<n); i++)
        my_subset(n, i);
    return 0;
}

输出结果为：

1
2
12
3
13
23
123

总结

本文主要介绍了用于生成子集的三种方法，其中增量构造法和位向量法采用递归枚举的思想，通过遍历对应的解答树求得子集，而二进制法通过类似于二进制"位与"的方法直接枚举出子集，过程更加的简单清晰。然而，递归枚举的方法虽然看起来没那么清晰，但其结题的思想确实非常重要的。实际上，采用递归的方法是一种更加通用的方法。