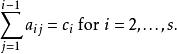1.龙格库塔法的基本原理
该算法是构建在数学支持的基础之上的。对于一阶精度的拉格朗日中值定理有:
对于微分方程
y'=f(x,y)
y(n+1)=y(n)+h*K1
K1=f(xn,yn)
当用点xn处的斜率近似值K1与右端点xn+1处的斜率K2的算术平均值作为平均斜率K*的近似值,那么就会得到二阶精度的改进拉格朗日中值定理:
y(n+1)=y(n)+[h*( K1+ K2)/2]
K1=f(xn,yn)
K2=f(x(n)+h,y(n)+h*K1)
依次类推,如果在区间[xn,xn+1]内多预估几个点上的斜率值K1、K2、……Km,并用他们的加权平均数作为平均斜率K*的近似值,显然能构造出具有很高精度的高阶计算公式。经数学推导、求解,可以得出四阶龙格-库塔公式,也就是在工程中应用广泛的经典龙格-库塔算法:
y(n+1)=y(n)+h*( K1+ 2*K2 +2*K3+ K4)/6
K1=f(x(n),y(n))
K2=f(x(n)+h/2,y(n)+h*K1/2)
K3=f(x(n)+h/2,y(n)+h*K2/2)
K4=f(x(n)+h,y(n)+h*K3)
注:
通常所说的龙格-库塔法是指四阶而言的,我们可以仿二阶、三阶的情形推导出常用的标准四阶龙格-库塔法公式
2.龙格-库塔(Runge-Kutta)方法
经典四阶法
在各种龙格-库塔法当中有一个方法十分常用,以至于经常被称为“RK4”或者就是“龙格-库塔法”。该方法主要是在已知方程导数和初值信息,利用计算机仿真时应用,省去求解微分方程的复杂过程。 [1]
令初值问题表述如下。
则,对于该问题的RK4由如下方程给出:
其中
这样,下一个值(yn+1)由现在的值(yn)加上时间间隔(h)和一个估算的斜率的乘积所决定。该斜率是以下斜率的加权平均:
k1是时间段开始时的斜率;
k2是时间段中点的斜率,通过欧拉法采用斜率k1来决定y在点tn+h/2的值;
k3也是中点的斜率,但是这次采用斜率k2决定y值;
k4是时间段终点的斜率,其y值用k3决定。
当四个斜率取平均时,中点的斜率有更大的权值:
RK4法是四阶方法,也就是说每步的误差是h阶,而总积累误差为h阶。
注意上述公式对于标量或者向量函数(y可以是向量)都适用。
显式法
显式龙格-库塔法是上述RK4法的一个推广。它由下式给出 [1]
其中
(注意:上述方程在不同著述中有不同但却等价的定义)。
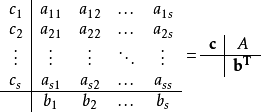
要给定一个特定的方法,必须提供整数s(级数),以及系数aij(对于1 ≤j<i≤s),bi(对于i= 1, 2, ...,s)和ci(对于i= 2, 3, ...,s)。
龙格库塔法是自洽的,如果
如果要求方法的精度为p阶,即截断误差为O(h)的,则还有相应的条件。这些可以从截断误差本身的定义中导出。例如,一个2级2阶方法要求b1+b2= 1,b2c2= 1/2, 以及b2a21= 1/2。
例子
RK4法处于这个框架之内。其表为:
0
1/2 1/2
1/2 0 1/2
1 0 0 1
_ 1/6 1/3 1/3 1/6
然而,最简单的龙格-库塔法是(更早发现的)欧拉方法,其公式为
。这是唯一自洽的一级显式龙格库塔方法。相应的表为:
0
_ 1
隐式方法
以上提及的显式龙格库塔法一般来讲不适用于求解刚性方程。这是因为显式龙格库塔方法的稳定区域被局限在一个特定的区域里。显式龙格库塔方法的这种缺陷使得人们开始研究隐式龙格库塔方法,一般而言,隐式龙格库塔方法具有以下形式:
其中
在显式龙格库塔方法的框架里,定义参数
的矩阵是一个下三角矩阵,而隐式龙格库塔方法并没有这个性质,这是两个方法最直观的区别:
需要注意的是,与显式龙格库塔方法不同,隐式龙格库塔方法在每一步的计算里需要求解一个线性方程组,这相应的增加了计算的成本。
龙格-库塔法的C语言实现
#include "stdio.h"
#include "stdlib.h"
void RKT(t,y,n,h,k,z)
int n; /*微分方程组中方程的个数,也是未知函数的个数*/
int k; /*积分的步数(包括起始点这一步)*/
double t; /*积分的起始点t0*/
double h; /*积分的步长*/
double y[]; /*存放n个未知函数在起始点t处的函数值,返回时,其初值在二维数组z的第零列中*/
double z[]; /*二维数组,体积为n x k.返回k个积分点上的n个未知函数值*/
{
extern void Func(); /*声明要求解的微分方程组*/
int i,j,l;
double a[4],*b,*d;
b=malloc(n*sizeof(double)); /*分配存储空间*/
if(b == NULL){
printf("内存分配失败\n");
exit(1);
}
d=malloc(n*sizeof(double)); /*分配存储空间*/
if(d == NULL){
printf("内存分配失败\n");
exit(1);
}
/*后面应用RK4公式中用到的系数*/
a[0]=h/2.0;
a[1]=h/2.0;
a[2]=h;
a[3]=h;
for(i=0; i<=n-1; i++)
z[i*k]=y[i]; /*将初值赋给数组z的相应位置*/
for(l=1; l<=k-1; l++){
Func(y,d);
for (i=0; i<=n-1; i++)
b[i]=y[i];
for (j=0; j<=2; j++){
for (i=0; i<=n-1; i++){
y[i]=z[i*k+l-1]+a[j]*d[i];
b[i]=b[i]+a[j+1]*d[i]/3.0;
}
Func(y,d);
}
for(i=0; i<=n-1; i++)
y[i]=b[i]+h*d[i]/6.0;
for(i=0; i<=n-1; i++)
z[i*k+l]=y[i];
t=t+h;
}
free(b);/*释放存储空间*/
free(d); /*释放存储空间*/
return;
}
main(){
int i,j;
double t,h,y[3],z[3][11];
y[0]=-1.0;
y[1]=0.0;
y[2]=1.0;
t=0.0;
h=0.01;
RKT(t,y,3,h,11,z);
printf("\n");
for (i=0; i<=10; i++){/*打印输出结果*/
t=i*h;
printf("t=%5.2f\t ",t);
for (j=0; j<=2; j++)
printf("y(%d)=%e ",j,z[j][i]); printf("\n");
}
}
void Func(y,d)double y[],d[];{
d[0]=y[1]; /*y0'=y1*/
d[1]=-y[0]; /*y1'=y0*/
d[2]=-y[2]; /*y2'=y2*/
return;
}