2019牛客暑期多校训练营（第一场）----D-Parity of Tuples

首先发出题目链接：
链接：https://ac.nowcoder.com/acm/contest/881/D
来源：牛客网
涉及：FWT(快速沃尔什变换)，容斥原理

点击这里回到2019牛客暑期多校训练营解题—目录贴

---

题目如下：


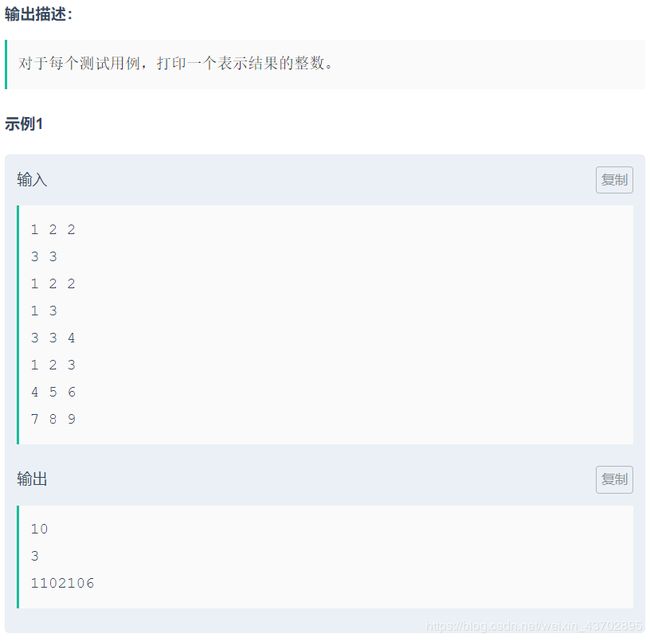
解释一下题目，每一个$v_i$都是一个一维数组，所以的$v_i$在一起，就变成了一个二维数组

还有$\wedge$符号就是$and$，按位与运算

---

首先定义$[a_i]$代表$a_i$这个数的二进制表示中1的数量。所以我们可以这样定义$count(x)$
$$count(x)=\frac{1}{2^m}\sum _{i=1}^n\prod _{j=1}^m(1-(-1{)}^{[v_{i,j}\&x]})$$
解释一波：

针对每一个i，只要$[v_{i,j}\&x]$都是奇数，那么$(1-(-1{)}^{[v_{i,j}\&x]})$就等于2，那么$\frac{1}{2^m}{\prod }_{j=1}^m(1-(-1{)}^{[v_{i,j}\&x]})$就等于1；

但是，只要有一个$[v_{i,j}\&x]$是偶数，那么${\prod }_{j=1}^m(1-(-1{)}^{[v_{i,j}\&x]})$就等于0

那么最后再将i从1到n求和，即${\sum }_{i=1}^n$，答案刚好就是$count(x)$的值

---

当然，连乘
$$\prod _{j=1}^m(1-(-1{)}^{[v_{i,j}\&x]})$$是可以展开的
$$\prod _{j=1}^m(1-(-1{)}^{[v_{i,j}\&x]})=(1-(-1{)}^{[v_{i,1}\&x]})(1-(-1{)}^{[v_{i,2}\&x]})...(1-(-1{)}^{[v_{i,m}\&x]})$$
$$=1-\sum _{a=1}^m(-1{)}^{[v_{i,a}\&x]}+\sum _{a=1}^m\sum _{b>a}^m(-1{)}^{[v_{i,a}\&x]+[v_{i,b}\&x]}-\sum _{a=1}^m\sum _{b>a}^m\sum _{c>b}^m(-1{)}^{[v_{i,a}\&x]+[v_{i,b}\&x]+[v_{i,c}\&x]}$$$$+...+(-1{)}^m(-1{)}^{{\sum }_{j=1}^m[v_{i,j}\&x]}$$
又因为（这条式子不懂的话，下面给出了证明）
$$(-1{)}^{{\sum }_{i=1}^n[a_i\&x]}=(-1{)}^{[x\&({\oplus }_{i=1}^n{a}_i)]}$$

---

这里来证明：
$$\sum _{i=1}^n[a_i\&x]与[x\&({\oplus }_{i=1}^n{a}_i)]奇偶性相同$$

异或的性质：
二进制相同位的数（0或1）相同（即同为0或同为1），则此位异或后的值为0，否则为1

假设当n=2，那么
$$(-1{)}^{{\sum }_{i=1}^n[a_i\&x]}=(-1{)}^{[a_1\&x]+[a_2\&x]}$$$$(-1{)}^{[x\&({\oplus }_{i=1}^n{a}_i)]}=(-1{)}^{[x\&(a_1\oplus a_2)]}$$

假设$[a_1\&x]=A$;$[a_2\&x]=B$

1.假设$a_1\&x$与$a_2\&x$的二进制表示中，没有相同位的数（0或1）相同，则
$$(-1{)}^{{\sum }_{i=1}^n[a_i\&x]}=(-1{)}^{[a_1\&x]+[a_2\&x]}=(-1{)}^{A+B}=(-1{)}^{[x\&(a_1\oplus a_2)]}$$
2.假设$a_1\&x$与$a_2\&x$的二进制表示中，有n对相同位的数（0或1）相同，则
$$(-1{)}^{{\sum }_{i=1}^n[a_i\&x]}=(-1{)}^{[a_1\&x]+[a_2\&x]}=(-1{)}^{A+B}$$$$(-1{)}^{[x\&({\oplus }_{i=1}^n{a}_i)]}=(-1{)}^{[x\&(a_1\oplus a_2)]}=(-1{)}^{A+B-2n}=(-1{)}^{A+B}$$
综上所述
$$\sum _{i=1}^n[a_i\&x]与[x\&({\oplus }_{i=1}^n{a}_i)]奇偶性相同$$故
$$(-1{)}^{{\sum }_{i=1}^n[a_i\&x]}=(-1{)}^{[x\&({\oplus }_{i=1}^n{a}_i)]}$$

---

证明完毕后，接着推导，故
$$=1-\sum _{a=1}^m(-1{)}^{[v_{i,a}\&x]}+\sum _{a=1}^m\sum _{b>a}^m(-1{)}^{[v_{i,a}\&x]+[v_{i,b}\&x]}-\sum _{a=1}^m\sum _{b>a}^m\sum _{c>b}^m(-1{)}^{[v_{i,a}\&x]+[v_{i,b}\&x]+[v_{i,c}\&x]}$$$$+...+(-1{)}^m(-1{)}^{{\sum }_{j=1}^m[v_{i,j}\&x]}$$$$=1-\sum _{a=1}^m(-1{)}^{[v_{i,a}\&x]}+\sum _{a=1}^m\sum _{b>a}^m(-1{)}^{[x\&(v_{i,a}\oplus v_{i,b})]}-\sum _{a=1}^m\sum _{b>a}^m\sum _{c>b}^m(-1{)}^{[x\&(v_{i,a}\oplus v_{i,b}\oplus v_{i,c})]}$$$$+...+(-1{)}^m(-1{)}^{[x\&({\oplus }_{j=1}^m{v}_{i,j})]}$$

这里就非常满足容斥定理公式的特点，可以用一个数组f存i从1到n时，所有$(-1)$的次数不同时所对应的系数，如下代码所示

inline void dfs(int *a,int num,int x,int mu){//a表示当前vi的一维数组，num表示考虑v(i,num+1)这个数是否容或者斥，x表示(-1)的此时的次数，mu表示(-1)^x的系数（只有1或者-1的可能，因为奇斥偶容）
	if(num==m){//表示已经考虑完了vi一维数组中的所有元素
		f[x]+=mu;//得到（-1）的次数为x的情况，将此时的系数加到f(x)中
		return;
	}
	dfs(a,num+1,x,mu);//表示-1的次数不需要异或上v(i,num+1)的情况
	dfs(a,num+1,x^a[num+1],-mu);//表示-1的次数需要异或上v(i,num+1)的情况
	return;
}

for(i=0;i<maxk+1;i++) f[i]=0;//先将系数关于-1次数的数组初始化
for(i=1;i<=n;i++){
	int a[m+5];
	for(j=1;j<=m;j++)	a[j]=read();//每次读入一个一维数组vi
	dfs(a,0,0,1);//读完就开始容斥，开始储存-1次数不同时的系数
}

---

容斥完毕之后，我们就得到了一个f数组，如上代码所示

这个f数组到底是啥意思捏，这么说吧，首先我们可以确定-1的所有次数可能小于题目中要求的1<所以f(0)存的是(-1)⁰的系数，f(1)存的是(-1)¹的系数…f(1<1<的系数。

按照$count(x)$的要求，凡是-1的次数z是奇次，那么-1^z就为-1，否则为1。

而现在主要的问题就是判断-1的次数是不是奇数或者偶数，现在f序列下标刚好是关于-1次数。

我们知道一个序列经过FWT_XOR变换后，得到的序列有一个特点

假如原序列是A，变换后是A’，那么
$$A^{\prime }[x]=\sum _{[x\&i]\mathrm{m}\mathrm{o}\mathrm{d}2=0}A[i]-\sum _{[x\&i]\mathrm{m}\mathrm{o}\mathrm{d}2̸=0}A[i]$$

很明显$$count(x)=f^{\prime }[x]=\sum _{[x\&i]\mathrm{m}\mathrm{o}\mathrm{d}2=0}f[i]-\sum _{[x\&i]\mathrm{m}\mathrm{o}\mathrm{d}2̸=0}f[i]$$
所以我们只需将容斥过后得到的f序列进行FWT_XOR变换，即可得到$count(x)$的值。关于FWT的知识可以看看其他博客

inline void FWT(){
	for(int i=1;i<(1<<k);i<<=1)
		for(int p=i<<1,j=0;j<(1<<k);j+=p)
			for(int h=0;h<i;++h){
				ll x=f[h+j],y=f[i+j+h];
				f[h+j]=(x+y)%mod;
				f[i+j+h]=(x-y+mod)%mod;
			}
}

得到了$count(x)$的值，$${\oplus }_{x=0}^{2^k-1}(count(x)\cdot 3^x\mathrm{m}\mathrm{o}\mathrm{d}(10^9+7))$$
的值就非常好求了，注意分数取模（还有一个$2^m$分母）和$3^x$的处理，可以像这样

ll three=1,inv=qpow(),res=0;//inv是逆元，分数取模的逆元
for(i=0;i<maxk;i++){
	res^=f[i]*three%mod*inv%mod;
	three=three*3%mod;
}

---

代码如下：

#include <iostream>
using namespace std;
typedef long long ll;
const int mod=1e9+7;//题目所给变量
int n,m,k,f[1<<21];//n,m,k均为题目所给变量，f数组存系数关于-1次数的序列，即f[x]为-1^x的系数。
inline int read(){
    int x=0,w=1;char ch=getchar();
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    if(ch=='-')w=0,ch=getchar();
    while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    return w?x:-x;
}
inline void FWT(){//FWT变化的代码，这里就不分析代码了
	for(int i=1;i<(1<<k);i<<=1)
		for(int p=i<<1,j=0;j<(1<<k);j+=p)
			for(int h=0;h<i;++h){
				ll x=f[h+j],y=f[i+j+h];
				f[h+j]=(x+y)%mod;
				f[i+j+h]=(x-y+mod)%mod;
			}
}
inline void dfs(int *a,int num,int x,int mu){//a表示当前vi的一维数组，num表示考虑v(i,num+1)这个数是否容或者斥，x表示(-1)的此时的次数，mu表示(-1)^x的系数（只有1或者-1的可能，因为奇斥偶容）
	if(num==m){//表示已经考虑完了vi一维数组中的所有元素
		f[x]+=mu;//得到（-1）的次数为x的情况，将此时的系数加到f(x)中
		return;
	}
	dfs(a,num+1,x,mu);//表示-1的次数不需要异或上v(i,num+1)的情况
	dfs(a,num+1,x^a[num+1],-mu);//表示-1的次数需要异或上v(i,num+1)的情况
	return;
}
inline ll qpow(){//快速幂求逆元
	ll pow=mod-2,x=1<<m,sum=1;
	while(pow!=0){
		if(pow%2==1)	sum=sum*x%mod;
		pow>>=1;
		x=x*x%mod;	
	}
	return (sum+mod)%mod;
}
int main(){
	while(~scanf("%d%d%d",&n,&m,&k)){
		int i,j,maxk=1<<k;//f数组（-1次数）的最大值
		for(i=0;i<maxk+1;i++) f[i]=0;//将系数关于-1次数的序列初始化
		for(i=1;i<=n;i++){
			int a[m+5];//每次创建一个数组
			for(j=1;j<=m;j++)	a[j]=read();
			dfs(a,0,0,1);//进行容斥，用f储存-1次数不同时的系数
		}
		FWT();//将f数组进行FWT_XOR变换，变换后的f序列即count(x)的序列
		ll three=1,inv=qpow(),res=0;//先把2^m逆元算出来
		for(i=0;i<maxk;i++){//这个循环是运算题目中那个异或表达式
			res^=f[i]*three%mod*inv%mod;
			three=three*3%mod;
		}
		printf("%lld\n",res);//注意此处不能再取模了
	}
	return 0;
}