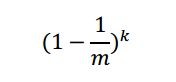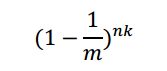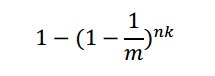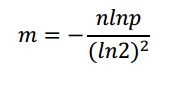布隆滤波器基本原理和pybloomfilter使用

1. 布隆滤波器原理

在日常开发过程中，会经常遇到元素是否存在集合判断和去重问题，例如我们会判断一个email地址是否在黑名单中，网络爬虫会判断一个url是否已经存在于待抓取列表或者已抓取，视频库的去重等等。不幸的是通常情况下这类问题面临的数据规模都较大，比如网络爬虫系统的抓取url通常达到数亿级别，如果采用哈希表存储这些url将会耗费大量的内存以至于在实际生产使用过程中几乎不可用，而布隆滤波器确实一种近乎完美的替代方案。（谨记：大部分的近似方案虽然会带来少量的损失，但是会给性能和效果带来极大的提升）

 

布隆过滤器（Bloom Filter）是由布隆（Burton Howard Bloom）在1970年提出的。它实际上是由一个很长的二进制向量和一系列随机映射函数组成，布隆过滤器可以用于检索一个元素是否在一个集合中。

 

布隆滤波器会有一个m位的bit数组（每位初始设为0）以及k个随机哈希函数，每个哈希函数的输出都是一个（0，m-1）之间的一个数（对应bit数组下标）。

添加操作：输入x，对于每一个哈希函数，计算j= hi(x)，将m_bit[j] 设成1；

查询操作：输入x，对于每一个哈希函数，计算j= hi(x)，如果m_bit[j] 不等于1，则说明x不在集合中，否则如果k个函数的映射位都为1，说明x存在于集合中。

 

布隆滤波器的优点是空间效率和查询时间都远远超过一般的算法，缺点是有一定的误识别率（假正例Falsepositives，即Bloom Filter判断某一元素存在于某集合中，但是实际上该元素并不在集合中）和删除困难，但是没有识别错误的情形（即假反例Falsenegatives，如果某个元素确实没有在该集合中，那么Bloom Filter 是不会报告该元素存在于集合中的，所以不会漏报）。

2.False-Positive推导

假设k个哈希函数完全随机，即以等概率选在（0，m-1）中的一个数，那么m_bit中某一位在添加元素时一次哈希没有被置位的概率是：

经过k次哈希没有被置位的概率是：

添加n个元素该位仍然没有被置位的概率是：

那么该位在添加n个元素后被置位的概率是：

现在对于一个新元素，要判断其是否在集合中，如果判断该元素存在于集合中，说明k个哈希位都为1，但是有可能会错误的把实际不存在于集合中判断为存在于集合中（False Positive），该事件发生的概率为：

 

可以看出随着m（位数组大小）的增加，False Positive概率会下降，同时随着插入元素个数 n 的增加，False Positives的概率又会上升。

 

对于给定的m、n，哈希函数的个数k的最优值为：

 

对于给定的False Positives概率 p和元素个数n，位数组m的最优值为：

推导略。

3. Pybloomfilter

 Pybloomfilter（https://axiak.github.io/pybloomfiltermmap/#）是一个用java实现的bloomfilter版本，为了兼顾效率，内部位数组使用C实现。

Pybloomfilter构造时允许传入capacity（即n），error rate，位数组大小（m），哈希函数个数（即k）以及一个序列化的nmap文件。

下面示例代码简单的展示了如何使用Pybloomfilter：

#! /usr/bin/env python
# -*- coding:utf-8 -*-

import os
import sys
reload(sys)
sys.setdefaultencoding('utf-8')

import random

from pybloomfilter import BloomFilter

# 创建一个capacity等于100万，error rate等于0.001的bloomfilter对象
bfilter = BloomFilter(1000000,0.001,'bf_test.bloom')

# 添加100个元素
for x in xrange(1000000):
    bfilter.add(str(x))

# 与nmap文件同步
bfilter.sync()


# 测试error rate
error_in = 0
for x in xrange(2000000):
    if str(x) in bfilter and x > 1000000:
        error_in += 1

print "error_rate:%s" % (error_in*1.0/1000000)

最终结果输出：

error_rate:0.001009；非常接近于我们设置值0.001。

 

4. 总结

布隆滤波器是利用很小的错误率代价完美实现了海量数据规模下的去重和判断问题，在平时的大数据研究和开发中，不要总为完美的解决方案而费尽心血，尝试多使用近似的替代方案。

 

 

参考：

https://github.com/axiak/pybloomfiltermmap

http://blog.csdn.net/u013467442/article/details/41150023

维基百科：布隆过滤器：http://zh.wikipedia.org/zh/%E5%B8%83%E9%9A%86%E8%BF%87%E6%BB%A4%E5%99%A8

数学之美二十一：布隆过滤器（Bloom Filter）：http://www.google.com.hk/ggblog/googlechinablog/2007/07/bloom-filter_7469.html